Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Кононов А.Н. 1 Миндеева А.А. 1 Петросян В.С. 1 Манукян А.А. 1

---

1 Национальный исследовательский университет «МИЭТ»

В настоящей статье были исследованы методы структурной оптимизации микроконвейерной архитектуры, основанные на использовании последовательно-параллельных бинарных диаграмм решений. Были рассмотрены схемы микроконвейерной архитектуры, спроектированные в базисе ПЛИС/СБМК. Оптимизация производилась при помощи программного комплекса, которое использует представление цифровой схемы в виде последовательно-параллельных бинарных диаграмм решений (Series-Parallel Binary Decision Diagrams – SP-BDD) и позволяет оптимизировать схему путем переупорядочения вершин SP-BDD. Основная идея предлагаемого авторами метода состоит в том, чтобы на время оптимизации удалить промежуточные регистры микроконвейера и объединить комбинационные фрагменты в одну комбинационную схему большего размера вместо того, чтобы оптимизировать их по отдельности. При оптимизации объединенной схемы пространство поиска является более разнообразным, чем при оптимизации ее частей по отдельности. Для каждой схемы были рассмотрены три варианта оптимизации: комбинационных фрагментов по отдельности, с объединением двух комбинационных фрагментов, с объединением всех комбинационных фрагментов. Приведены результаты тестирования в виде таблицы. В результате эксперимента самым эффективным подходом к оптимизации оказался метод с объединением всех комбинационных фрагментов, который привел к повышению быстродействия (укорочение критического пути) до 3,5 раза и уменьшения размеров (количества транзисторов) до 44,5 процентов.

Статья в формате PDF

309 KB

оптимизация схем

оптимизация микроконвейеров

двоичные решения

оптимизация комбинационных схем; оптимизация цифровых схем

1. Актуальные проблемы моделирования в системах автоматизации схемотехнического проектирования / А.Л. Глебов, М.М. Гурарий, М.М. Жаров и др. – М.: Наука, 2003. – 430 c.

2. Глебов А.Л. SP-BDD цифровых КМОП схем и ее приложения в оптимизации и моделировании // Информационные технологии. – 1997. – № 10. – C. 18–22.

3. Кононов Н.А. Структурная оптимизация и обфускация цифровых схем в базисе ПЛИС / СБМК // Lambert Academic Publishing, Germany. – 2011.

4. Строганов А. Проектирование комбинационных схем в базисе ПЛИС // Компоненты и технологии. – 2008. – № 5. – С. 148–153.

5. Glebov A.L., Blaauw D., Jones L.G. Transistor reordering for low power CMOS gates using SP-BDD representation // Intern. Symp. On Low Power Design – Dana Point CA, 1995. – P. 161–166.

6. Glebov A.L., Gavrilov S.V., Blaauw D. et.al. Library-less synthesis for static CMOS circuits // ICCAD-97. – 1997. – P. 461–467.

7. Mohideen S.K., Perinbam J.R. An effective Asynchronous Micropipeline using Double edge triggered D Flip Flop // International Journal of Applied Engineering and Research, India. – 2007. – Vol. 2, № 1. – P. 139–146.

8. Sutherland I.E. Micropipelines // Communications of ACM. – 1989. – Vol. 32. – P. 720–738.

Понятие микроконвейера первоначально введено в 1989 году И. Сазерлендом в качестве архитектуры для асинхронных схем [8]. Асинхронный микроконвейер схематически изображен на рис. 1.

Микроконвейер состоит из линейной последовательности регистров (на рис. 1 – R1, R2, R3, R4) и комбинационных схем (на рис. 1 – CL3, CL4), вычисляющих некоторые системы Булевых функций. Поскольку схема асинхронная, она не имеет единого тактового сигнала, и работа каждой пары соседних регистров синхронизируется с помощью контрольной логики (CTL), реализующей механизм «handshaking» (рукопожатие).

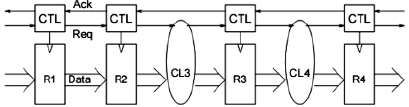
Рис. 1. Асинхронный микроконвейер

Существует также синхронный аналог микроконвейера, изображенный на рис. 2.

Архитектура микроконвейера выбрана не случайно. Дело в том, что в форме микроконвейера может быть представлена практически любая цифровая схема, как синхронная, так и асинхронная [7].

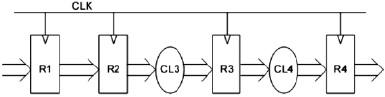
Рис. 2. Синхронный аналог микроконвейера

Оптимизация микроконвейерной архитектуры

В данной работе предложен метод оптимизации цифровых схем, имеющих архитектуру микроконвейера, основанный на использовании диаграмм двоичных решений специального вида. Были рассмотрены схемы микроконвейерной архитектуры, спроектированной в базисе ПЛИС/СБМК [4]. Указанный базис содержит однотипные универсальные логические модули (УЛМ), каждый из которых может вычислять произвольную Булеву SP (последовательно-параллельную) функцию, имеющую не более четырех аргументов [3]. Указанная Булева функция реализована в виде поисковой таблицы (LUT). Кроме того, УЛМ содержат элементы памяти, которые могут быть использованы для формирования регистров микроконвейера.

Предлагаемый метод структурной оптимизации микроконвейера основан на использовании программы структурной оптимизации комбинационных цифровых КМОП схем OPTI, использующей внутреннее представление цифровой схемы в виде SP-BDD [5, 2].

При обработке SP-BDD представления схемы используются следующие алгоритмы:

• Экстракция SP-BDD из транзисторной схемы.

• Переупорядочение вершин (транзисторов КМОП вентиля).

• Слияние двух SP-BDD (двух КМОП вентилей).

• Декомпозиция SP-BDD (КМОП вентиля).

• ПП-сужение (разложение Шеннона для SP-BDD).

• Минимизация SP-BDD (КМОП вентиля) [6, 1].

Основная идея предлагаемого метода оптимизации следующая. С одной стороны, каждую комбинационную схему в микроконвейере (CL3, CL4, рис. 2) можно оптимизировать по отдельности. С другой стороны, можно на время оптимизации удалить регистр R3 и объединить схемы CL3, CL4 в одну комбинационную схему большего размера. После оптимизации этой схемы она может быть вновь «разрезана» (если это необходимо) на две составные части CL3’, CL4’, и между ними может быть вставлен соответствующий регистр R3’. В случае оптимизации объединенной схемы пространство поиска является более разнообразным, чем при оптимизации ее частей по отдельности, поэтому результат оптимизации может быть более сильным.

В исследовании был также проведен эксперимент при условии объединения в единую комбинационную схему более двух отдельных комбинационных схем вплоть до одновременной оптимизации всего микроконвейера.

Целью эксперимента ставилось сравнение полученных результатов и выявление самого эффективного подхода.

В качестве исходного использовался набор комбинационных схем, содержащий некоторые из схем ISCAS-85, а также ряд фрагментов промышленных схем. Каждая из исходных схем после отображения в базис ПЛИС/СБМК была преобразована в микроконвейерную схему посредством упорядочения универсальных логических модулей (УЛМ), декомпозиции на четыре равные по размеру части и добавления пяти регистров необходимой разрядности.

После этого обработка (оптимизация) каждого микроконвейера выполнялась в трех вариантах:

– каждый из четырех комбинационных фрагментов обрабатывался отдельно;

– перед обработкой комбинационные фрагменты объединялись попарно с временным удалением промежуточного регистра;

– вся комбинационная часть микроконвейера обрабатывалась целиком с временным удалением всех промежуточных регистров.

После обработки во втором и третьем вариантах все промежуточные регистры необходимой разрядности были снова добавлены в схему.

Ниже приведены результаты численных экспериментов по оптимизации микроконвейерных схем с использованием этих подходов. В таблице приведены результаты сравнения исходных и трех вариантов оптимизированных микроконвейерных схем.

В первой колонке указаны исследуемые схемы. Во второй и третьей колонке соответственно исходный размер (под размером в данном случае понимаем количество поисковых таблиц в комбинационной части схемы, «Р» в таблице) и исходное быстродействие, то есть минимальный период («МП» в таблице) тактового сигнала, на котором может работать схема. В данном случае под минимальным периодом понимается максимальная длина критического пути комбинационного фрагмента микроконвейера, вычисленная в предположении единичной задержки каждого УЛМ. Три варианта оптимизации в таблице обозначены соответственно Опт. 1, Опт. 2, Опт. 3. Результаты эксперимента в для трёх вариантов оптимизации представлены соответственно в колонках 4, 6, 7, 9, 10, 12. Проценты уменьшения размера («%» в таблице) в результате оптимизации схем представлены в колонках 5, 8, 11.

Результаты эксперимента

Из приведенной таблицы видно, что для всех тестируемых схем оптимизация приводит к уменьшению размера, в ряде случаев значительному (максимальное значение для одной схемы ‒ 44,5 %). Быстродействие схем во всех случаях значительно (для одной схемы в 3,5 раз) улучшается, в том числе с укрупнением оптимизируемых фрагментов. Для сравнения, для тех же схем по первым двум вариантам оптимизации были получены следующие результаты: уменьшение размера на 27,1 % в первом варианте, на 29,3 % во втором, увеличение быстродействия в 1,4 раза в первом варианте, в 1,75 раза.

Заключение

Описанный метод структурной оптимизации во всех случаях дал положительный результат. Для всех 10 схем, использованных в эксперименте, самым эффективным оказался метод с объединением всех комбинационных фрагментов микроконвейерной архитектуры, который привел к уменьшению размера схем до 44,5 % и увеличению быстродействия до 3,5 раз.

Таким образом, предлагаемый метод оптимизации микроконвейерных схем обладает высокой эффективностью (отчасти связанной с используемым алгоритмом структурной оптимизации цифровых КМОП схем). Полученные результаты доказывают практическую ценность данного метода оптимизации микроконвейерной архитектуры, спроектированной в базисе ПЛИС/СБМК.

Рецензенты:

Глебов А.Л., д.т.н., профессор, старший научный сотрудник, Национальный исследовательский университет «МИЭТ», Зеленоград, г. Москва;

Адамов Ю.Ф., д.т.н., профессор, ведущий научный сотрудник, Институт проблем проектирования в микроэлектронике Российской академии наук, Зеленоград, г. Москва.

Работа поступила в редакцию 12.03.2013.

Библиографическая ссылка