Формирование стратегии устойчивого развития экономической системы должно основываться на оптимальных управленческих решениях. В связи с этим возникает необходимость решения задачи оптимального экономического роста с целью выбора определенной стратегии управления, обеспечивающей оптимальные пропорции между потреблением и накоплением.
Сформулируем задачу экономического роста в условиях открытой региональной экономики как задачу максимизации благосостояния населения с заданным горизонтом планирования. В основе подхода лежит классическая макромодель Рамсея-Касса-Купманса (РКК-модель) [1-3].
Предполагается, что для развития производства используются как собственные, так и заемные средства. Любой кредит характеризуется своей величиной P, процентной ставкой σ, периодом реализации 
, периодом погашения n и временем поступления кредита tp.
Будем полагать, что все показатели кредита известны за исключением времени поступления кредитов - данный показатель выбран в качестве одного из управляющих параметров.
Пусть 
- вектор моментов времени поступлений m кредитов. Тогда расчет в текущем периоде времени за кредиты обозначим 
; сумму кредитов, поступивших в текущий момент времени - 
.
Для более точного моделирования расходов и доходов будем различать производящее население L(t) (трудовые ресурсы) и потребляющее население экономической единицы L°(t) (население в целом). Динамика численности различных групп населения была получена в виде прогнозных кривых в работах [4, 5].
Технологические возможности системы описываются заданной производственной функцией f(k). Произведенный продукт (в удельных, на работающего, единицах) y=f(k)≥0 делится на три неотрицательные, рассчитанные на душу населения части, одна из которых инвестируется в производство, другая идет на потребление, третья - на выплату процентов по кредитам:
,
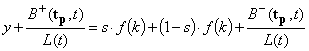где S - норма накопления, выступающая как переменная управления.
Фазовой координатой системы является фондовооруженность труда k≥0 (отношение объема фондов к численности работников, k = K / L), динамика которой с учетом процесса инвестирования описывается соотношением ,
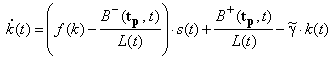
где 
экзогенно заданная функция времени, отражающая совокупное действие двух факторов - выбытие фондов и изменение трудовых ресурсов: 
, η - коэффициент износа фондов.
В интервал времени от t0 до t1 благосостояние W, соответствующее траектории благосостояния на одну демографическую единицу, определяется интегрированием всех мгновенных полезностей по всему интервалу. В качестве переменной, характеризующей полезность от экономического функционирования какого-либо региона, выберем потребление как величину, отражающую жизненный уровень населения. Для того чтобы иметь возможность складывать полезности, соответствующие разным моментам времени, их необходимо привести к текущему моменту, для чего введем норму дисконтирования. Положим, что дисконтирующий множитель имеет вид экспоненты: 
[6,7].
Задача максимизации благосостояния населения с учетом инвестиционных процессов формулируется следующим образом:
Целевой функционал
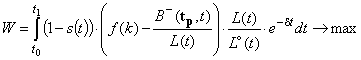, (1)
при условиях:
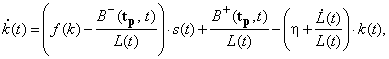(2)
, (3)
, (4)
, (5)
где 
- вектор сроков погашения m кредитов.
Для решения задачи оптимизации (1)-(5) может быть применен численный подход, развитый в работах [8-10].
СПИСОК ЛИТЕРАТУРЫ
- Ramsey P.P. A Mathematical theory of savings. Econ. Journ., 1928, v.38, N 152, pp. 543-559.
- Cass D. Optimum growth in an aggregative model of capital accumulation. Review of of Econ. Studies, 1965, 32, pp. 233-240.
- Koopmans T.C. On the concept of optimal economic growth. Ex Aedibus Academicis in Civitate Vaticana, 1965, 28, pp. 225-300.
- Русяк И.Г., Кетова К.В. Математическое моделирование демографических показателей. - В сб. статей ИжГТУ, 2002, Ижевск.
- Русяк И.Г., Кетова К.В. Анализ точности прогнозирования демографических показателей. - Материалы научно-практической конференции,ИжГТУ, 2002, Ижевск.
- Интрилигатор М. Математические методы оптимизации и экономическая теория. - М.: Прогресс, 1975. - 606 с.
- Столерю Л. Равновесие и экономический рост. - М.: Статистика, 1974. - 472 с.
- Евтушенко Ю.Г. Методы решения экстремальных задач и их применение в системах оптимизации. - М.: Наука, 1982. - 432 с.
- Тененев В.А., Паклин Н.Б. Гибридный генетический алгоритм с дополнительным обучением лидера // Интеллектуальные системы в производстве. - 2003. - № 2. - Ижевск: Изд-во ИжГТУ, 2003. - с. 181-206.
- Батищев Д.И. Генетические алгоритмы решения экстремальных задач //под ред. Львовича Я.Е.: Учеб. пособие. - Воронеж, 1995.