Для оценки состояния биологического объекта особое значение приобретает динамика внутрисердечной гемодинамики, а также функция отдельных элементов при различной степени недостаточности митрального клапана. С появлением быстродействующих вычислительных машин математическое моделирование не раз применялось в качестве инструмента для изучения динамики кровотока в норме и при патологии митрального клапана [1, 2, 3]. В литературе известны математические модели нормальной гемодинамики митрального клапана, однако в представленных моделях гемодинамики рассматривается только часть сердечного цикла без учета патологии клапана. Математическая модель внутрисердечной гемодинамики McQueen имела ряд недостатков: модель представлена двумерной и анализировала только систолический период кардиоцикла [1]. Уравнения модели Szabó, 2004 не позволяли моделировать весь период сердечного цикла [4]. В исследованиях Einstein, 2005; Kunzelman, 2007 описана модель трехмерной реконструкции митрального клапана без математического описания функционального состояния левого желудочка и предсердия [2, 3].
Представленная работа призвана внести свой вклад в актуальную проблему диагностики заболеваний сердечно-сосудистой системы по данным ультразвуковых исследований и упреждению патологии, непосредственно связанной с риском возникновения тяжелых осложнений.
Учитывая вышеназванные ограничения, нами разработана математическая модель внутрисердечной гемодинамики с учетом степени митральной недостаточности, сократительной функции левого желудочка и предсердия. В работе использовано уравнение Хилла для описания динамики сокращения желудочков и предсердия. Другие параметры функционирования сердца (эластичность миокарда, характерные времена процесса) определялись по данным ЭКГ и гемодинамики сердца. Предложенная математическая модель позволяет исследовать влияние патологии клапана на внутрисердечную гемодинамику. Полученные результаты математического моделирования сопоставлены с данными клиническо-экспериментальных исследований внутрисердечной гемодинамики. Описание математической модели включает уравнения динамики сокращения миокарда и гемодинамические уравнения.
Уравнения динамики сокращения миокарда.
Опишем динамику сокращения миокарда с помощью уравнения Хилла [5], устанавливающего связь между напряжением мышцы P и скоростью ее сокращения v:
(1)
где Pmax - максимальное изометрическое напряжение, vmax - максимальная скорость изотонического сокращения, c - безразмерный коэффициент, колеблющийся в пределах от 0,25 до 0,4 [6]. В рассматриваемом случае напряжение Pmax и скорость сокращения vmax сердечной мышцы являются функциями объема камеры, а Pmax является функцией числа деполяризованных клеток
(2)
Аппроксимируя данные работы [6] параболой, запишем f(v) как:
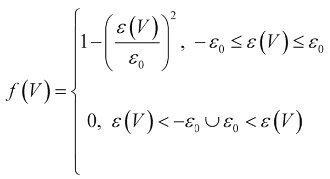(3)
где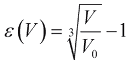 
- относительное удлинение миокарда, V0 - объем камеры, при котором сократительная способность миокарда максимальна, ε0 - значение относительного удлинения, за пределами которого миокард теряет способность к сокращению.
Для установления связи между напряжением миокарда и давлением в полостях сердца рассмотрим сферу радиуса r, окруженную стенкой толщиною h, состоящей из мышечных волокон, развивающей в каждой точке мускульное напряжение P и связанное с эластичностью пассивное напряжение Pe в направлении волокон. Таким образом, в любой точке стенки полное напряжение в направлении волокон равно P + Pe, а средняя величина полного напряжения в любом направлении, перпендикулярном проходящей через рассматриваемую точку и центр сферы прямой, равна
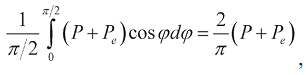
где φ - угол между направлением мышечных волокон и рассматриваемым направлением. Рассечем весь сферический слой проходящей через его центр плоскостью на две равные полусферы. Согласно третьему закону Ньютона, сила мускульного напряжения, действующая между полусферами, равна силе, действующей на внутреннюю поверхность желудочка:
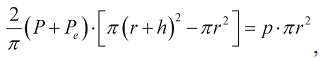
где p - давление внутри камеры. Вводя объем полости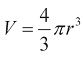 
и массу миокарда 
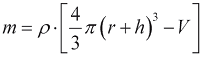, где ρ - плотность миокарда, получаем:
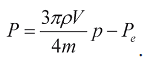(4)
Зависимость пассивного напряжения Pe от относительного удлинения λ на основании данных работы [6] определяется уравнением
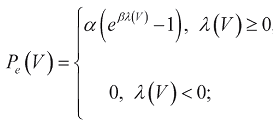(5)
где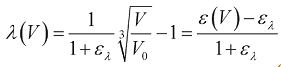 
- относительное удлинение миокарда (в отличие от относительного удлинения ε формулы (3), отсчитываемого относительно V0, λ отсчитывается относительно (1+ελ)3V0), ελ - значение относительного удлинения ε, за пределами которого пассивное напряжение отсутствует, α и β - коэффициенты, определяющие эластичность ткани.
Гемодинамические уравнения
Пренебрегая изменением формы полости, уравнение имеет вид:
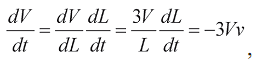(6)
где L - линейный размер полости. С другой стороны,
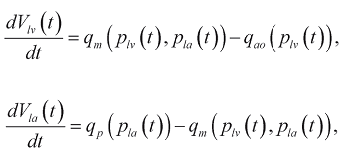(7)
где расходы крови в малом круге кровообращения q p(p 1a) через митральный qm(p1v,p1a) и аортальный клапаны qao(p1v) в соответствии с формулой Пуазейля равны:
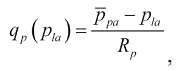(8a)
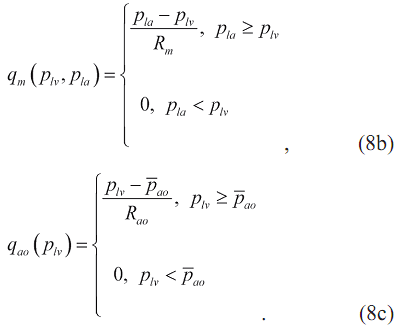
Здесь ̅ppa и ̅pao - средние давления в легочной артерии и аорте, Rp, Rm и Rao - гидродинамические сопротивления малого круга кровообращения, митрального и аортального клапанов.
Гидродинамическое сопротивление малого круга кровообращения равно отношению разности средних давлений в легочной артерии и ЛП к минутному объему крови: Rp = (15 - 7) мм рт.ст.·с : 7 л/мин ~ 0,07 мм рт.ст.·с/мл.
Уравнения трансмитральной гемодинамики. С учетом уравнений (2, 4, 6, 7) уравнения (1) приобретают следующий вид:
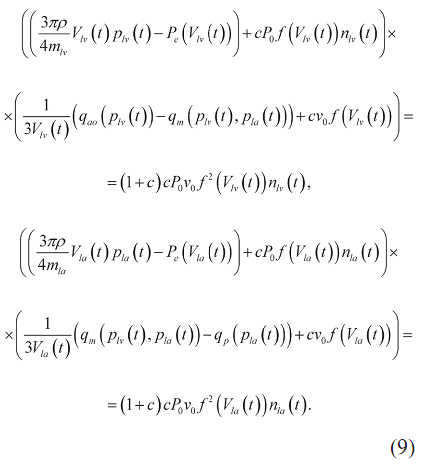
Четыре уравнения системы (7, 9) содержат объемы V1v(t), V1a(t) и давления p1v(t), p1a(t) в качестве неизвестных функций, а также семь функций (n1v(t), n1a(t), f(V), Pe(V), qp(p1a), qm(p1v,p1a), qao(p1v)), выраженных уравнениями (3, 6, 8, 9). Неизвестные функции найдены путем интегрирования дифференциальных уравнений (7) методом Эйлера с пошаговым численным решением алгебраических уравнений (9) методом сопряженного градиента, вычисленных с использованием начального значения вида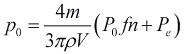 
. Начальные условия дифференциальных уравнений (7) получены из требований периодичности:
V1v(0)=V1v(T) и М1a(0)=V1a(T).
В настоящем исследовании проводилось сопоставление клинико-экспериментальных данных с результатами математического моделирования. Для этого было обследовано 76 детей с ПМК, 45 девочек и 31 мальчик. В зависимости от степени патологии сердца все дети были разделены на 2 группы: I - 37 детей с умеренной митральной регургитацией (MR), фракция регургитирующего объема (RF) < 30 %); II - 39 пациентов с выраженной MR (30 % < RF <47 %). Эхокардиография (ЭхоКГ) выполнялась по общепринятой методике [7] в одномерном и двухмерном режимах на аппарате «Vivid 7» (GE). При ЭхоКГ определяли диаметр и объем левого и правого предсердий, конечно-систолический и диастолический размеры полости левого и правого желудочков. Также оценивались тип гемодинамики, ударный объем, фракция выброса, толщина миокарда ЛЖ. По данным цветового допплеровского картирования определялась степень MR. Расчет фракции регургитирующего объема (RF) проводился с использованием уравнения непрерывности потока [7].
Использование математического моделирования в клинической кардиологии позволит повысить качество диагностики нарушений гемодинамики при недостаточности митрального клапана, определить тактику ведения больного и провести отбор пациентов для хирургической коррекции порока.
Выводы
1. Разработана математическая модель трансмитральной гемодинамики с учетом патологии элементов клапана, описывающая процесс в систоло-диастолический период.
2. Предложенная математическая модель позволяет оценивать динамику параметров внутрисердечной гемодинамики, включая ударный объем, фракцию выброса, колебания давления и трансмитральный расход крови.
СПИСОК ЛИТЕРАТУРЫ
-
McQueen D.M., Peskin C.S., Yellin E.L. Fluid dynamics of the mitral valve: physiological aspects of a mathematical model.// Am. J. Physiol. (1982) 242, H1095-H111O.
-
Einstein D.R., Kunzelman K.S., Reinhall P.G., Nicosia M.A., Cochran R.P. Nonlinear fluid-coupled computational model of the mitral valve.// J. Heart Valve Dis. (2005) 14. - С. 376-385.
-
Kunzelman K.S., Einstein D.R., Cochran R.P. Fluid-structure interaction models of the mitral valve: function in normal and pathological states.// Phil. Trans. R. Soc. B (2007) 362. - С. 1393-1406.
-
Szabó G., Soans D., Graf A., Bellera C.J., Waite L., Hagl S. A new computer model of mitral valve hemodynamics during ventricular filling.// Eur. J. Cardio-thoracic Surgery (2004) 26. - С. 239-247.
-
Hill A.V. The heat of shortening and the dynamic constants of muscle.// Proc. R. Soc. B (1938). - 126, с. 136-195.
-
Волькенштейн М.В. Физика мышечного сокращения Успехи физ. наук. - 1970, 100, №- 4, с. 681-703.
-
Фейгенбаум Х. Клиническая эхокардиография. 2007. - 620 с.