Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Поэтому особую актуальность приобретает проблема компьютерного моделирования и решение задач по созданию информационных систем поддержки принятия управленческих решений. Основу таких систем должны составлять сложные математические модели, которые должны адекватно отображать сложность исследуемой системы управления и, прежде всего, ее многоцелевой характер. Отсюда следует, что в основе таких моделей должны лежать многокритериальные задачи оптимизации и разработка эффективных алгоритмов их решения является важнейшей задачей, как системного анализа вообще, так и компьютерного моделирования в частности. В данной работе предлагается общая классификация векторных (многокритериальных) задач и алгоритм их решения, который, как нам кажется, должен стать ядром современных информационных систем бизнес - планирования и управления.

2. Многочисленные примеры постановок важных практических задач векторной оптимизации из разных областей [1-3] говорят о различии, в первую очередь, их математических моделей. Поэтому, для разработки эффективного алгоритма их решения необходимо дать некоторые общие определения и провести общую классификацию векторных задач.

Пусть заданы: - множество элементов любой природы (которые в конкретных задачах могут быть названы вариантами решениями, управления и т.д.); - множество элементов, называемых перечнем или списком качественных свойств элементов множества ; - множество -мерных вещественных функций. Тогда множество отображений  в :

называется множеством целевых функционалов, которые отражают различные целевые устремления элементов множества .

Пусть также даны  - целевые функционалы, которые также будем называть локальными или частными критериями; элементы множества , соответствующие элементам , где - элементы множества  - являются -мерными вещественными векторами, а - элементы множества  - являются вещественными числами. Тогда вектор из множества

,

координатами которого являются локальные критерии множества , называется вектор-функцией цели или векторной целевой функцией. Она является многоцелевым показателем качественных устремлений элементов множества .

Определение 1. Общей векторной задачей математического программирования (общей ВЗМП) называется задача, которая состоит в определении оптимального по Парето множества , в каждой точке которого  - значения векторной целевой функции удовлетворяют условиям:

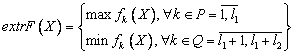(2.1)

при ограничениях

(2.2)

(2.3)

где:  - вектор искомого варианта решения (управления);

 - вектор функций-ограничений;

 - вектор, определяющий уровень ограничений.

Будем считать, что - вогнутые, а - выпуклые функции относительно  так, что область допустимых решений  не является пустым множеством:

(2.4)

Очевидно, что вариант решения

 представляет собой координаты - мерного вещественного вектора на множестве .

Определение 2. Вариант решения  общей ВЗМП называется оптимальным по Парето (Парето-оптимальным), если на множестве допустимых решений  не существует такого варианта решения , для которого выполнялись бы неравенства

(2.5)

(2.6)

и хотя бы одно из них было строгим.

Определение 3. Совокупность точек оптимальных по Парето называется Парето-оптимальным множеством.

Определение 4. Совокупность чисел , удовлетворяющих ограничениям задачи (2.2) - (2.3), называется допустимым решением общей ВЗМП.

Определение 5. Допустимое решение общей задачи ВЗМП , при котором вектор-функция (2.1) принимает свое Парето-оптимальное значение, называется компромиссным решением общей ВЗМП.

Исходя из постановки общей задачи векторной оптимизации, любую из многочисленных ВЗМП можно свести к одному из следующих типов, в соответствии с выбранными признаками - классификаторами.

1. По характеру отношений предпочтения между критериями:

a) равнозначные ВЗМП - в которых количественно не определяется отношений предпочтения между критериями, т.е. считаем их все равноценными;

b) неравнозначные ВЗМП - где определяется приоритет каждого критерия с помощью количественных оценок отношений предпочтения.

2.По характеру оптимизации каждого критерия:

a) однородные ВЗМП - в которых все локальные критерии - - оптимизируются одинаково (либо max, либо min);

b) неоднородные ВЗМП - где часть локальных критериев - - максимизируется, для остальных - - ищется минимум.

3. По виду целевых функций и функций-ограничений :

a) линейные ВЗПМ - все и линейны относительно ;

b) нелинейные ВЗМП - хотя бы одна из или является нелинейной.

4. По типу переменных :

a) непрерывные ВЗМП - все могут принимать любые неотрицательные, действительные значения;

b) дискретные ВЗМП - все (или частично) могут быть любыми из некоторого дискретного множества, в частности, целых чисел;

c) стохастические ВЗМП - в которых все (или частично) принимают некоторые значения лишь с определенной вероятностью.

3. Для решения векторных задач представленных в общей классификации предлагается алгоритм, основанный на методе гарантированного результата и нормализации критериев (ГРНК). Он сводит векторную задачу к скалярной задаче оптимизации, но отличается от большинства других методов доказательством существования и единственности получаемого оптимального решения по Парето [4] и тем, что его можно использовать для решения векторных задач различных классов (как линейных, так нелинейных и дискретных). Представим его в виде следующей итеративной схемы.

Шаг 1. Решить  (по общему числу критериев) задач скалярной оптимизации (известными методами математического программирования):

и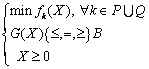

и найти и , .

Шаг 2. Выполнить единую нормализацию критериев :

или (2.7)

Шаг 3. Построить  - или  - задачу:

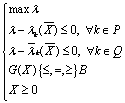 или .

Шаг 4. Решить  - или  - задачу как скалярную задачу оптимизации и найти единственную точку , оптимальную по Парето, в которой гарантируем результат:

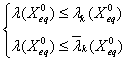или .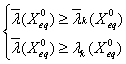

Шаг 5. Зная величину нормализованного критерия в точке , по формулам (2.7) найти необходимые значения каждого критерия , т.е. решить равнозначную задачу векторной оптимизации.

Кроме того, метод ГРНК позволяет решать неравнозначные векторные задачи с приоритетом некоторого критерия, выбранного ЛПР (лицом, принимающим решения) с целью улучшить его значение. При этом уровень приоритета, можно сказать, вычисляется с помощью коэффициентов приоритета, а не назначается ЛПР субъективно, как в подавляющем числе других методов решения векторных задач. Для решения векторной задачи с неравнозначными критериями необходимо, в общем случае, выполнить следующие шаги.

Шаг 6. Решаем соответствующую векторную задачу с равнозначными критериями. ЛПР проводит анализ результатов решения и, по величине , определяет s - критерий, значение которого необходимо улучшить.

Шаг 7. Вычисляются пределы изменения коэффициента приоритета s - критерия по отношению к остальным:

,

где , ,   , , а координаты и  найдены на шаге 1.

Шаг 8. ЛПР выбирает необходимую величину  в установленных пределах и, если  строит  - или  - задачу в форме:

или ,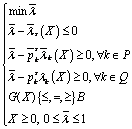

решая которую, как скалярную задачу оптимизации, находит точку компромиссного решения , где достигается результат:

 или

Если , то, выбрав точно также , необходимо построить  - или  - задачу в форме:

или ,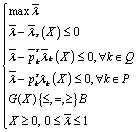

решая которую, как скалярную задачу оптимизации, аналогично найти точку компромиссного решения .

Шаг 9. Найти компромиссные значения каждого критерия и .

Модификации алгоритма данного метода для решения линейных, нелинейных и дискретных задач будут заключаться в различии способов решения соответствующих скалярных задач оптимизации на шагах 1, 4 и 9. Таким образом, предлагаемый метод ГРНК, используя распространенные методы решения задач скалярной оптимизации, может достаточно легко встраиваться в различные алгоритмы принятия решений и, по нашему мнению, должен стать основой современных информационных систем управления.

СПИСОК ЛИТЕРАТУРЫ

1. Мезенцев Ю.А., Кириллов Ю.В. Некоторые аспекты задач оптимального проектирования при нескольких критериях предпочтения. // Сб. науч. трудов НГТУ, 2003, №3, стр. 21-40.
2. Кириллов Ю.В. Использование методов векторной оптимизации в современных информационных технологиях управления.//Стратегия бизнеса и социально-экономическое развитие региона: Сб. статей участников 6-й Всерос. науч.-практ. конференции, Ярославль, 27 ноября 2003. - Ярославль: Ремдер, 2003. - с. 748 -753.
3. Kirillov Yu., Shestakova A. Optimization of a price policy with using of vector-stochastic models. / Modelling, Computation and Optimization in Information Systems and Management Sciences MCO 2004.: Fifth International conference on Computer Science. July 1-3, 2004, Metz University, France.
4. Иванов Л.Н., Кириллов Ю.В. К вопросу о Парето-оптимальности решений задач векторной оптимизации // Сб. науч. трудов НГТУ, 2003, №3, стр. 61-74.