Задача определения математического ожидания случайного нестационарного процесса, решаемая при обработке данных в современных информационно-измерительных комплексах, идентична задаче сглаживания случайной составляющей, которая предполагается стационарной. При выборе того или иного метода обработки данных необходимо исходить из возможности получения несмещенных, эффективных и состоятельных оценок математического ожидания, простоты аппаратурной реализации алгоритма обработки и возможности проведения анализа в реальном масштабе времени. В наибольшей степени перечисленным требованиям отвечает оператор скользящего среднего. Кроме того, данный оператор одновременно с вычислением оценок математического ожидания допускает выполнение операции центрирования.
Оценка математического ожидания, полученная с помощью оператора скользящего среднего, в общем случае, является смещенной. В качестве меры погрешности оценки математического ожидания можно использовать среднеквадратическую ошибку (СКО): 
. Первое слагаемое равно дисперсии оценки математического ожидания и характеризует долю случайной составляющей в значении ошибки. Систематическая составляющая ошибки 
зависит от аддитивной детерминированной составляющей исследуемого случайного процесса 
.
На рисунке 1. приведены графики зависимости максимальной СКО оценки математического ожидания от интервала усреднения для аддитивно - мультипликативной модели 
при 
и различных законах изменения мультипликативной составляющей 
, при этом z(t) - стационарный случайный процесс с нулевым математическим ожиданием Представленная модель рассматривалась на длине реализации, равной периоду составляющей φ1(t), в каждой точке отсчета рассчитывалась СКО. Анализ полученных результатов показал, если математическое ожидание изменяется по периодическому закону, то существует оптимальный интервал усреднения, при котором максимальная ошибка на всей длине реализации будет наименьшей. Оптимальный интервал усреднения зависит от скорости нарастания математического ожидания, определяемой значением 
.
В таблице представлены экспериментально полученные зависимости оптимального интервала усреднения и соответствующие зависимости СКО от интервала дискретизации, который выбирался из условия 
.
Проведенные исследования показали, что законы изменения мультипликативной составляющей практически не влияют на выбор интервала усреднения, отмечено более заметное их влияние на величину СКО.
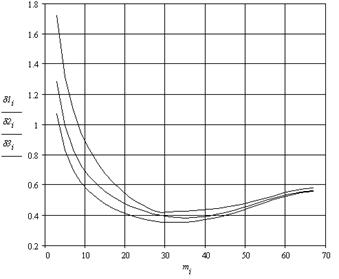
Рисунок 1. Зависимость максимальной СКО оценки математического ожидания от интервала усреднения (δ1: φ2(t)= 2 - exp(-8t); δ2: φ2(t)= 2 - cos(-28πt); δ3: φ2(t)= 1+5t))
Таблица 1. Зависимость интервала усреднения и СКО от интервала дискретизации
|
Значение f, Гц |
Интервал усреднения m |
СКО |
|
1 |
0,862188*(Dt)-0,796739 |
2,3874*(Dt)0,395262 |
|
4 |
0,29401*(Dt)-0,785338 |
3,7724*(Dt)0,395565 |
|
14 |
0,102316*(Dt)-0,779936 |
4,99992*(Dt)0,396067 |
|
40 |
0,0373379*(Dt)-0,792728 |
6,70392*(Dt)0,397507 |
Для случая, когда аддитивная составляющая наблюдаемого процесса изменяется по нелинейному непериодическому закону, СКО уменьшается по мере увеличения интервала усреднения.
Операция центрирования нестационарного по математическому ожиданию процесса, представленного аддитивно-мультипликативной моделью, приводит его к процессу с отличным от нуля математическим ожиданием. Оценка математического ожидания центрированного процесса имеет синусоидальный характер, амплитуда зависит от интервала сглаживания, дисперсия оценки математического ожидания соизмерима с дисперсией исходного процесса, определяемой детерминированной составляющей φ2(t) и случайной составляющей z(t).