В некоторых случаях при анализе фотоснимков поверхности Земли, полученных обычным способом, на предмет выявления каких-либо аномалий и определения их геометрических характеристик последние или вообще не различимы даже человеком или отличия лежат в пределах допустимых статистических отклонений, что не позволяет с достаточной степенью надежности выявить возможные аномалии [3]. Изображения этих же зон земной поверхности, сделанные с помощью щелевого многополосного спектрометра, позволяют сопоставить каждой точке изображения набор спектральных отсчетов, размер которого определяется числом полос спектрометра. Последующий анализ полученных спектральных изображений может повысить надежность выделения аномалий, их идентификацию и определение геометрических характеристик.
Одна из проблем, возникающая при обработке спектральных изображений - значительный большой объем информации, непрерывно поступающей от устройства ввода. Желательно понизить его без существенной потери информативности.
Если считать каждую спектральную полосу признаком объекта, относящегося к некоторому классу, то можно рассматривать эту проблему как задачу выявления наиболее информативных признаков. В качестве возможного решения может быть использован критерий информативности Фишера [4]
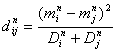 , (1)
, (1)
где ![]() - значение критерия по n-ому признаку для пары классов i и j,
- значение критерия по n-ому признаку для пары классов i и j, ![]() - математические ожидания и дисперсии по n-ому признаку для классов i и j. Критерий (1) позволяет выбрать наиболее информативный признак для пары классов с учетом статистических характеристик разброса значений каждого признака для сравниваемых классов. Естественно, для эффективного применения этого критерия необходимо наличие репрезентативной выборки спектральных отсчетов пикселов для каждой из возможных аномалий. Применение данного метода на спектральных изображениях, адекватно моделирующих возможные реальные аномалии, показало возможность 30% сокращения объема необходимой информации без существенного снижения качества распознавания.
- математические ожидания и дисперсии по n-ому признаку для классов i и j. Критерий (1) позволяет выбрать наиболее информативный признак для пары классов с учетом статистических характеристик разброса значений каждого признака для сравниваемых классов. Естественно, для эффективного применения этого критерия необходимо наличие репрезентативной выборки спектральных отсчетов пикселов для каждой из возможных аномалий. Применение данного метода на спектральных изображениях, адекватно моделирующих возможные реальные аномалии, показало возможность 30% сокращения объема необходимой информации без существенного снижения качества распознавания.
Учитывая большое число признаков и их статистический характер, наиболее эффективным представляется использовать в качестве параметра классификации минимальное расстояние Махаланобиса [4] в пространстве признаков
![]() ,(2)
,(2)
где ri - расстояние до i-го класса, ![]() вектор признаков распознаваемого образа,
вектор признаков распознаваемого образа, ![]() вектор математических ожиданий i-го класса, Сi-1 - обратная матрица ковариации для вектора признаков i-го класса.
вектор математических ожиданий i-го класса, Сi-1 - обратная матрица ковариации для вектора признаков i-го класса.
Классификация по расстоянию (2) позволяет учесть статистические параметры всей совокупности признаков. Применение данного метода для вяления аномалий показало вполне допустимую степень надежности распознавания (около 80%). Сокращение числа распознаваемых классов за счет априорной информации о возможных аномалиях на конкретном изображении позволяет для некоторых сочетаний аномалий повысить степень распознаваемости до 95%.
После распознавания, т.е. отнесения подавляющего большинства пикселов изображения к тому или иному классу объектов, естественно возникает необходимость определения геометрических характеристик каждого из распознанных объектов, например, площади. Вопрос определения истинных геометрических характеристик объекта фактически сводится к проблеме компенсации пространственных искажений изображения, связанных с взаимным расположением объекта и устройства получения изображения. Если оптическая ось устройства при съемке направлена вертикально вниз, то необходимо компенсировать только масштабные искажения, что не вызывает сложностей при наличии информации о расстоянии до поверхности Земли в момент съемки. Более сложным является вопрос компенсации пространственных искажений изображения объекта при его получении устройством бокового обзора. Использование подобных устройств особенно актуально при анализе возможных аномалий, т.к. в некоторых случаях нахождение «летающей лаборатории» непосредственно над аномалией не представляется целесообразным.
Для определения геометрических характеристик объекта и возможно сравнения его с «эталонным» изображением можно использовать аппарат теории групп. Как известно [5] , преобразование изображения объекта при изменении взаимного расположения самого объекта и устройства получения изображения описывается при условии центрального проецирования проективной группой
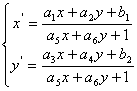 ,(3)
,(3)
где:![]() исходные и преобразованные проективной группой координаты точки изображения,
исходные и преобразованные проективной группой координаты точки изображения, ![]() параметры проективной группы. При параллельном проецировании преобразование изображения описывается аффинной группой - частным случаем проективной, для которой a5=a6=0.
параметры проективной группы. При параллельном проецировании преобразование изображения описывается аффинной группой - частным случаем проективной, для которой a5=a6=0.
В каждом конкретном случае все точки изображения ![]() подвергаются преобразованию
подвергаются преобразованию ![]() одним и тем же элементом группы
одним и тем же элементом группы ![]() , т.е. параметры
, т.е. параметры ![]() группы постоянны при преобразования всех точек изображения. Следовательно, для приведения искаженного изображения к исходному виду достаточно найти параметры обратного преобразования g-1 и применить его к искаженному изображению, компенсируя тем самым пространственные искажения. Общая процедура устранения на изображениях перспективных и иных искажений описана и обоснована в работе [6].
группы постоянны при преобразования всех точек изображения. Следовательно, для приведения искаженного изображения к исходному виду достаточно найти параметры обратного преобразования g-1 и применить его к искаженному изображению, компенсируя тем самым пространственные искажения. Общая процедура устранения на изображениях перспективных и иных искажений описана и обоснована в работе [6].
Метод полной одновременной компенсации искажения, описываемого аффинной или проективной группой, обеспечивается использованием так называемых «реперных» точек или просто «реперов» на изображении. Из уравнений (3) видно, что при наличии информации о координатах нескольких точек на исходном и преобразованном изображениях и их взаимном соответствии можно определить параметры как прямого, так и обратного преобразования, решив линейную систему уравнений. Для аффинной группы необходимое число этих точек, называемых «реперными», - три и, соответственно, необходимо решить систему из шести линейных уравнений, для проективной группы число «реперов» - четыре, а решить необходимо систему уже из восьми линейных уравнений. Заметим, что для проективной группы уравнения относительно коэффициентов группы остаются линейными, хотя уравнения, описывающие преобразование таковыми не являются.
Если искажению подвергается изображение плоского объекта, то оно полностью описывается, как максимум, проективной группой, но в случае объемного изображения, например многогранника, искажение изображения каждой из видимых граней будет описываться проективной группой со своими коэффициентами. Применительно к аэрофотоснимкам это означает, что, если высота какого-либо объекта на земной поверхности представляет собой значительную величину по сравнению с высотой до точки съемки, то следует как-то учесть эту особенность. Одним из возможных решений может быть представление преобразования в виде кусочно-проективного или кусочно-аффинного [7]. Для этого следует выделить на исходном изображении достаточное количество «реперных» точек и разбить все изображение или только часть, содержащую аномалии, на треугольные фрагменты, используя в качестве вершин выбранные «реперы». Компьютерное моделирование данного метода показало, что разбиение на треугольники, т.е. представление преобразования в виде кусочно-аффинного, более эффективно, с точки зрения автоматизации, без существенной потери точности представления.
В качестве «реперов» естественно использовать малоразмерные и хорошо различимые объекты. На поверхности Земли это могут быть перекрестки дорог, мосты, отдельно стоящие здания, деревья или их компактные группы, характерные по форме участки береговой черты или речного русла. Однако, решение проблемы поиска и идентификации «реперов» непосредственно на аэрофотоснимке в автоматическом режиме в общем случае вызывает серьезные затруднения. Использование для решения этой задачи оператора приводит к резкому увеличению как времени обработки. В качестве альтернативы можно предложить автоматизировать поиск и идентификацию «реперных» точек на основании спектральной информации.
Если «реперы» имеют различные спектры, то их идентификация фактически заканчивается в момент распознавания по этим спектрам в соответствии с расстоянием (2) в пространстве признаков. Если различные «реперы» относятся к одному классу в пространстве спектральных признаков, то их дальнейшую идентификацию можно проводить известными методами распознавания, используя изображения на аэрофотоснимке. Учитывая малые размеры объектов, используемых в качестве «реперов», можно ограничиться искажениями типа смещения, изменения масштаба и поворота. Методы компенсации таких искажений и выбора признаков, инвариантных к некоторым из них, известны [6].
Программная реализации методов обработки аэрофотоснимков [8] имеют свои особенности. Групповые преобразования (3) относятся к разряду непрерывных, т.е. не только коэффициенты ![]() могут принимать действительные значения, но и координаты
могут принимать действительные значения, но и координаты ![]() тоже могут принимать действительные значения, естественно в определенных пределах. Очевидно, последнее невозможно для компьютерного представления изображения. Видимо следует различать абстрактное представление изображения как гладкой непрерывной действительной функции двух переменных
тоже могут принимать действительные значения, естественно в определенных пределах. Очевидно, последнее невозможно для компьютерного представления изображения. Видимо следует различать абстрактное представление изображения как гладкой непрерывной действительной функции двух переменных ![]() , значения которой представляют яркость изображения в точке с координатами
, значения которой представляют яркость изображения в точке с координатами ![]() . В таком случае естественно использовать термин «точка изображения», подчеркивая тем самым, что речь идет о не имеющем собственного размера элементе изображения. Представление изображения в компьютере носит принципиально дискретный характер. Под изображением понимается матрица, значение элемента которой соответствует яркости некоторой области поля зрения устройства получения изображения и, следовательно, носит интегральный характер. Естественно, номер элемента матрицы может быть только целым числом, да и значения элемента, хотя и могут представляться в действительной форме, как правило, представляются в целочисленной форме. Представляется оправданным использовать в таком случае термин «пиксел» изображения, подчеркивая наличие конечных размеров у «точки» изображения.
. В таком случае естественно использовать термин «точка изображения», подчеркивая тем самым, что речь идет о не имеющем собственного размера элементе изображения. Представление изображения в компьютере носит принципиально дискретный характер. Под изображением понимается матрица, значение элемента которой соответствует яркости некоторой области поля зрения устройства получения изображения и, следовательно, носит интегральный характер. Естественно, номер элемента матрицы может быть только целым числом, да и значения элемента, хотя и могут представляться в действительной форме, как правило, представляются в целочисленной форме. Представляется оправданным использовать в таком случае термин «пиксел» изображения, подчеркивая наличие конечных размеров у «точки» изображения.
В рассмотренном выше методе компенсации пространственных искажений описываемых групповыми преобразованиями предложено определять коэффициенты обратного преобразования и последовательно применять его к точкам искаженного изображения, приводя его тем самым к исходному виду. Непосредственная реализация этого метода на компьютере приводит к некоторым проблемам. Представление изображения как непрерывной функции фактически означает наличие взаимно однозначного соответствия между точками исходного и искаженного изображения, которое и описывается групповым преобразованием. Естественно, следует исключить вырожденные случаи - преобразование изображения в точку или линию, как не имеющие практического значения. Представление изображения в виде матрицы не дает возможности говорить о взаимно однозначном соответствии между пикселами исходного и преобразованного изображений. Как следствие, применение обратного преобразования к искаженному изображению приводит в общем случае к появлению на восстановленном изображении пропусков в виде незаполненных пикселов. Применение тех или иных методов аппроксимации для их заполнения, приводит с одной стороны к усложнению алгоритма восстановления, а с другой - к уменьшению резкости восстановленного изображения, хотя и без изменения контрастности, что может в дальнейшем снизить надежность распознавания. Под резкостью изображения в данном случае понимается разность яркости соседних пикселов, а под контрастностью - разность максимальной и минимальной яркости на изображении. Понятно, что чем выше резкость изображения, тем точнее можно определить контур изображения, а, как известно [2], именно контур несет максимум информации о распознаваемом объекте.
Представляется более оправданным при компьютерной реализации процесса компенсации пространственных искажений, описываемых групповым преобразованием, находить коэффициенты именно прямого преобразования. После их вычисления следует найти для всех пикселов восстанавливаемого изображения соответствующие им пикселы на искаженном изображении и присвоить им найденные значения яркости. В таком случае никаких пропусков в восстановленном изображении не будет и, следовательно, не потребуется их заполнение. Соответственно и резкость для соседних пикселов восстановленного изображения не будет меньше, чем на искаженном изображении. Практическая реализация предложенного алгоритма показала вполне удовлетворительное качество восстановления изображения с точки зрения его надежности распознавания имеющихся на нем образов.
Описанный выше метод был использован для определения характеристик аномалий земной поверхности (области радиоактивного или химического заражения местности, учета природных ресурсов и т.п.) с привязкой этих новых объектов к карте местности, а также для выбора оптимальных маршрутов движения автономного мобильного робота на неизвестной пересеченной местности.
СПИСОК ЛИТЕРАТУРЫ
- Мошкин В.И., Петров А.А., Титов В.С. и др. Техническое зрение роботов. М., Машиностроение, 1990, 272с.
- Марр Д. Зрение. Информационный подход. М., Радио и связь, 1987, 400с.
- Ту Дж., Гонсалес Р., Принципы распознавания образов. М.: Мир, 1978, 411с.
- Дистанционное зондирование: количественный подход. Под ред. Ф.Свейна и Ш.Девис. Пер. с англ. М., Недра, 1983, 396с.
- Файн В.С. Опознавание изображений. Основы непрерывно-групповой теории и ее применение. М., Наука, 1970, 296с.
- Ерош И.Л., Игнатьев М.Б., Москалев Э.С. Адаптивные робототехнические системы (методы анализа и системы обработки изображений). Л., ЛИАП, 1985, 144 с.
- Ерош И.Л. Восстановление рельефа неровной поверхности по плоскому изображению и реперным точкам. "Экстремальная робототехника", вып.VII. СПб., СПбГТУ, 1998г, с. 235-239.
- 8.Ерош И.Л., Гладкова И.Г., Соловьев Н.В. Программная реализация методов обработки и анализа аэрофотоснимков. В сб. Теория и практика создания систем технического зрения. М., 1990, с.64-67.



