In the canonical Periodical systems of elements (Mendeleev´s system) all elements are sorted by their ascending atomic numbers (Z) which is confirmed by Moseley´s law deduced on the basis of examination of characteristic X-ray radiation of the elements.
Mendeleev who based on the Periodic law discovered by himself sorted out this sequence into periods (altogether 7 periods) (and called his system the periodic one) and he further divided large periods (beginning with Period 4) into horizontal lines (altogether 11 lines).
Besides, the elements of the horizontal lines are divided into 8 groups (vertical columns of the Table). Thus, each element of the Table finds itself at the intersection of a horizontal line and a column which form the element coordinates.
The period and group number in this case is actually of a formal nature; is lacks a clear (well-defined) criterion. Period 1 consisting of two elements does not fit the pattern at all; besides, it is the only unpaired period. And for such elements like lanthanoids and actinoids no room was found in the canonical Table and they were placed under it. There are some other shortcomings in the canonical periodical system; and it´s not a surprise that a great number of attempts are made to work out a more perfect form of the periodic table.
Below the results of the author´s work performed within the period of 1973-31.08.1991 are presented The author´s system is based on the free (neutral) atom (for the sake of simplicity in the form of the most stable isotope) and quantum numbers obtained from examination of the intrinsic unique linear optical spectrum which determine its stable quantum state.
Let´s start from well-known facts and look at the periodic table studied at school. For each element in the table its electron configuration is stated (for example, for hydrogen - 1s1, which is the written statement of the fact that the quantum number is n = 1, the orbital quantum number is l = 0, and in the electron shell on this quantum energetic sublevel there is one electron).
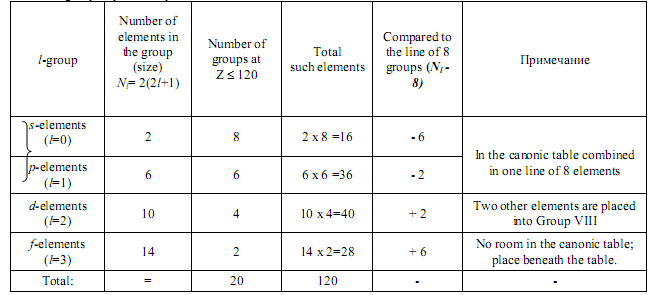
In the canonical table each element´s cell has one of the four colours according to the particular orbital quantum number, and the elements are arranged as groups of sequential elements: s-elements (l=0), p-elements (l=1), d-elements (l=2), f-elements (l=3) etc (named in the appearance order). Altogether there are 20 such groups at Z≤ 120.
It is also known that the number of electrons in the atom is the same as its atomic number Z, which means that in each subsequent element on one of the outer shells another electron appears. The quantum state of this electron is defined according to Pauli´s exclusion principle (1925, established on the basis of spectra examination) by a particular set of 4 quantum numbers (n, l, ms, ml), which determines the quantum state of the atom as a whole. Presently to such quantum numbers are defined for all know elements due to spectrum examination of the neutral atom (i.e. the atom in the isolated state).
Change of the particular set of quantum numbers for a certain element results in the change of the aggregate quantum numbers recorded usually in the form of a so called spectral term also specific for each of the known elements (see J.Amsley; Elements, Moscow, Mir, 1993).
The meaning of the defined quantum numbers is not yet clearly understood. For example, they are never mentioned to characterize the elements even in the most recent editions of the physical and chemical encyclopedias. Instead, when characterizing the element, the encyclopedias describe the physical and chemical properties of the elementary substance which are really important for praxis but still secondary.
The quantum numbers are parameters of the quantum state of the neutral atom (not changing with time) and are defined by analysis of the atom spectrum which is strictly individual for each particular atom, i.e. is its "visiting card". Many elements were discovered just by their spectra. Understanding of the physical meaning of quantum numbers is the way to creation of the atom theory (only a model for the time being); and the atom theory and the theory and form of presentation of the periodic system of elements are the two sides of the same medal. They develop in parallel and benefit to each other.
However, let´s have a look at the canonic table again. We shall note that all the elements are distributed into l-groups painted to different colours. Altogether there are 4 types of such groups (see Table 1). They are:
1) s-elements (i.e. l = 0) - elements of Groups I and II (alkaline and alkaline-earth elements) (in horizontal lines 1,2,3,4,6,8 and 10).
2) p-elements (i.e. l = 1) - elements of Groups III-VIII (in lines 2,3,5 and 7).
3) d-elements (i.e. l =2) - elements of Groups III-VIII (in 4,6,8 and 10)
and Groups I and II (in lines 5, 7 and 9), i.e. broken into two lines.
4) f-elements (i.e. l=3) - no room for them in the table; they are places beneath it (lanthanoids and actinoids).
Table 1. l-group of periodic system of elements at Z ≤ 120
The sequence of all 20 l-groups by ascending quantum energetic levels is determined from the spectra of free atoms. These groups are combined into larger (n+l)-groups according to Klechkovsky´s rules (1900-72) (see Table 2).
Table 2. (n+l)-periods and their pairs (dyads) at Z ≤ 120
|
Dyad No. М |
(n+l)-groups (periods) |
Number of l-groups in the period |
Composition of (n+l)-group |
lmax = |
Size of (n+l)-period Nn+l = 2M2 |
|
1 |
1st and 2nd |
1 |
s-elements only |
0 |
2 |
|
2 |
3d and 4th |
2 |
p-эelements, s-elements |
1 |
8 |
|
3 |
5th and 6th |
3 |
d-elements, p-elements,s-elements |
2 |
18 |
|
4 |
7th and 8th |
4 |
f-elements, d-elements, p-elements, s-elements |
3 |
32 |
|
|
|
Total: 10 х 2=20 |
|
|
|
On the basis of the above factors the author suggests a new graphic form of the table - symmetrical quantum periodical system of elements, in which:
1) A period is actually a (n+l)-group, and all the periods as well as all groups are paired. Each pair of periods is a dyad.
2) Each line is one of l-groups (s-, p-, d-, f-elements). To the left end of each line the last element of the previous line is attached as an initial atom. Each line begins and ends with the element with 1So spectral term.
3) All lines are symmetrical against the central atom of the line which finishes the first half of l-group.
4) At the very top of the table there is a free neutron which is at the same time the initial element of the first line.
Then in the suggested form of the table the set of 4 quantum numbers makes the coordinates of each particular atom:
- The sum (n + l) means the period to which the atom belongs;
- The quantum number l means the line - the particular l-group to which the atom belongs;
- The spin quantum number ms (with its mark) indicates in which half of the table (left or right) the atom is to be found.
- The magnet quantum number ml (with its mark) points to a particular line where the atom is to be found. Thus, a group of such table (unlike a group in the canonical table) is a number of atoms with the same quantum numbers l and ml, and Klechkovky´s coordination index Ek .
The group number is determined by belonging to a certain l-group and by the number of electrons which joined this quantum energetic level. Accordingly, the first group of alkaline metals (plus hydrogen) gets the designation s1, the second group of earth metals - s2, etc.
The suggested table which reflects the above structural principles is presented in Table 2 the form of which:
- has minimum differences from the canonical;
- is saved from many shortcomings of the canonical table;
- fits with up-to-date science progress;
- is promising for further extending of atom structure knowledge and periodic system theory;
- serves as the basis for better understanding of physical and chemical properties of both the atoms and their compounds;
- due to its comprehensibility can be used to advantage for teaching purposes.
The suggested form of the table was developed by the author in 1973-1991. More detailed information is on the above issues can be found in the following publication: .F.Makhov, Symmetrical Quantum Periodic System of Elements, Moscow, 1997 ( a limited edition of 200 copies) ISBN 5-86700-027-3.



