Если на тело массы , находящегося на гладкой горизонтальной поверхности, действует постоянная сила F, направленная под некоторым углом к горизонту и при этом тело перемещается на некоторое расстояние S, то говорят, что сила F совершила работу A. Величину работы определяют по формуле [1,2,3]:
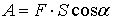(1)
Однако в природе идеально гладких поверхностей не бывает, и на поверхности контакта двух тел всегда возникают силы трения. Вот как об этом пишется в учебнике [1, Стр. 200]: «Работа силы трения покоя равна нулю, поскольку перемещение отсутствует. При скольжении твердых поверхностей сила трения направлена против перемещения. Ее работа отрицательна. Вследствие этого кинетическая энергия трущихся тел превращается во внутреннюю - трущиеся поверхности нагреваются».
Автором данной статьи было просмотрено множество школьных и вузовских учебников и задачников, но работа против сил трения рассматривалась только применительно к равномерному движению:
(2)
где μ - коэффициент трения скольжения.
Только в учебнике О.Д. Хвольсона [3, стр. 92] рассмотрен случай ускоренного движения при наличии сил трения: «Итак, следует отличать два случая производства работы: в первом сущность работы заключается в преодолевании внешнего сопротивления движению, которое совершается без увеличения скорости движения тела; во втором - работа обнаруживается увеличением скорости движения, к которому внешний мир относится индифферентно.
На деле мы обыкновенно имеем соединение обоих случаев: сила 
преодолевает какие-либо сопротивления и в то же время меняет скорость движения тела.
(*)
Работа r=fS состоит из двух частей: f´S тратится на преодолевание внешнего сопротивления, ρ на увеличение скорости тела».
Представим это в современной интерпретации (рис. 1). На тело массы m действует сила тяги FT, которая больше силы трения 
. Работу силы тяги в соответствии с формулой (*) можно записать так
(3)
где 
- сила, вызывающая ускоренное движение тела в соответствии со II законом Ньютона: 
. Работа силы трения отрицательна, но здесь и далее мы будем использовать силу трения и работу трения по модулю. Для дальнейших рассуждений необходим численный анализ. Примем следующие данные: m=10 кг; g=10 м/с2; FT=100 Н; μ=0,5; t=10 с. Проводим следующие вычисления: 
Н; 
Н; 
м/с2; 
м/с; 
кДж; 
м; 
кДж; 
кДж. Таким образом суммарная работа 
кДж
А теперь рассчитаем работу силы тяги FT для случая, когда трение отсутствует (μ=0 ). Проводя аналогичные вычисления, получаем: a=10 м/с2; V=100м/с; K=5 кДж; S=500 м; A=50 кДж. В последнем случае за те же 10 с мы получили работу в два раза больше. Могут возразить, что и путь в два раза больше. Однако, что бы ни говорили, получается парадоксальная ситуация: мощности, развиваемой одной и той же силой, отличаются в два раза, хотя импульсы сил одинаковы 
кН×с. Как писал М.В. Ломоносов еще в 1748 г.: «...но все изменения, совершающиеся в природе, происходят таким образом, что сколько к чему прибавилось столько же отнимется у другого...». Поэтому попробуем получить другое выражение для определения работы.
Запишем II закон Ньютона в дифференциальной форме:
(4)
и рассмотрим задачу о разгоне первоначально неподвижного тела (трение отсутствует). Интегрируя (4), получим: 
. Возведя в квадрат и разделив на 2m обе части равенства, получим:
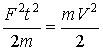или A=K (5)
Таким образом, получили другое выражение для вычисления работы
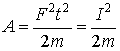(6)
где 
- импульс силы. Это выражение не связано с путем S, пройденным телом за время t, т.е. оно может быть использовано для вычисления работы, совершаемой импульсом силы и в том случае, если тело остается неподвижным, хотя, как утверждают во всех курсах физики, в этом случае никакой работы не совершается.
Переходя к нашей задаче об ускоренном движении с трением, запишем сумму импульсов сил:
, где 
; 
; 
.
Возведя в квадрат сумму импульсов, получим:
Разделив все члены равенства на , получим:
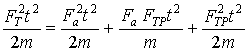(7)
или
где 
- работа, затрачиваемая на ускорение; 
- работа, затрачиваемая на преодоление силы трения при равномерном движении, а 
- работа, затрачиваемая на преодоление силы трения при ускоренном движении. Численный расчет дает следующий результат: 
кДж, т.е. мы получили ту же самую величину работы, которую совершает сила FT при отсутствии трения.
Рассмотрим более общий случай движения тела с трением, когда на тело действует сила F, направленная под углом α к горизонту (рис. 2). Теперь сила тяги 
, а силу 
- назовем силой левитации, она уменьшает силу тяжести 
, а в случае 
тело не будет оказывать давления на опору, будет находиться в квазиневесомом состоянии (состоянии левитации). Сила трения 
. Силу тяги можно записать в виде 
, а из прямоугольного треугольника (рис. 2) получим: 
. Умножая последнее соотношение на t2, получим баланс импульсов сил, а разделив на 2m, получим баланс энергий (работ):
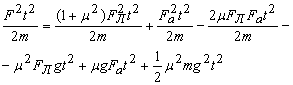(8)
Приведем численный расчет для силы F=100 Н и 
при тех же условиях ( m=10 кг; μ=0,5; t=10 с.). Работа силы F будет равна 
, а формула (8) дает следующий результат (с точностью до третьего знака после запятой):
50=15,625+18,974-15,4-12,5+30,8+12,5 кДж.
Как показывают расчеты, сила F=100 Н, действуя на тело массы m=10 кг под любым углом α за 10 с совершает одну и ту же работу 50 кДж.
Последний член в формуле (8) представляет собой работу силы трения при равномерном движении тела по горизонтальной поверхности со скоростью 
(9)
Таким образом, под каким бы углом не действовала данная сила F на данное тело массы , при наличии трения или без него, за время t будет совершена одна и та же работа (даже если тело неподвижно):
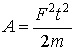(10)
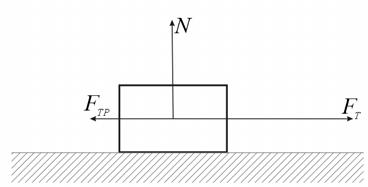
Рисунок 1.
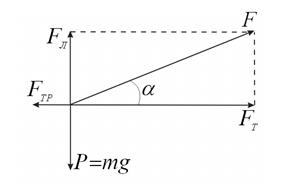
Рисунок 2.
СПИСОК ЛИТЕРАТУРЫ
- Матвеев А.Н. механика и теория относительности. Учеб.пособие для физ.спец.вузов. - М.: Высш.шк., 1986.
- Стрелков С.П. Механика. Общий курс физики. Т. 1. - М.: ГИТТЛ, 1956.
- Хвольсон О.Д. Курс физики. Т. 1. РСФСР Госуд.Изд-во, Берлин, 1923.