В настоящее время в медицинской диагностике для анализа функционального состояния головного мозга человека широкое распространение получил метод вызванных потенциалов головного мозга. Вызванными потенциалами (ВП) головного мозга называют электрические сигналы мозга, возникающие в ответ на стимуляцию нервных окончаний. Регистрация сигнала ВП осуществляется с головы человека на фоне шумов измерения и сигнала спонтанной активности головного мозга. Наиболее распространённым методом выделения ВП в настоящее время является метод когерентного усреднения, позволяющий регистрировать низкоамплитудные сигналы ВП, амплитуда которых не превышает 15 мкВ при отношении сигнал/шум менее 1/5. Но данный метод имеет ряд недостатков, таких как сравнительно большое время выделения сигнала ВП, что неприменимо в условиях операционного мониторинга, сглаживание характеристик сигнала ВП в результате многократного накопления, а также дополнительное искажение сигнала ВП в следствие привыкания человека к многократной стимуляции.
Для устранения указанных недостатков метода когерентного усреднения при выделении ВП, в литературе показана возможность использования для этих целей метода линейной нестационарной фильтрации. Такой метод позволяет выделять сигнал ВП в реальном масштабе времени и достоверность выделяемого сигнала повышается за счет применения многоканальной обработки сигнала при использовании векторной нестационарной фильтрации. Учитывая, что сигнал ВП имеет гауссовско-марковский характер и регистрируемые вместе с сигналом помехи (формирующий шум и шум измерения) являются гауссовскими с нулевым математическим ожиданием, векторную модель сигнала ВП можно представить разностными уравнениями сообщения и наблюдения:
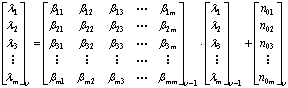, (1)
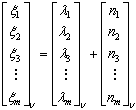. (2)
В этих уравнениях 
- матрица-столбец значений амплитуды напряжения сигнала ВП на 
-м отсчете, 
- матрица-столбец значений амплитуды напряжения сигнала ВП на (
)-м отсчете,
, 
- матрицы последовательности взаимно-независимых белых гауссовских шумов, 
- матрица коэффициентов связи размерностью ( 
), m - количество каналов съема.
При задании модели сигнала ВП в такой форме, основной проблемой является определение следующих параметров: матрицы коэффициентов связи и матрицы шума . Таким образом, при m-канальном съеме сигнала ВП, количество неизвестных параметров (m2+m). В опубликованных ранее работах при применении векторной нестационарной фильтрации для выделения ВП, параметры модели сигнала были определены для частного случая. В данной работе ставится задача определения параметров векторной модели сигнала ВП в общем случае.
Принимая во внимание, что параметром сигнала ВП, задающим основные его характеристики, является матрица коэффициентов , а индивидуальные особенности человека отражены в матрице формирующего шума , обобщим векторную модель сигнала ВП для нескольких пациентов. Тогда, учитывая, что связи между каналами разных пациентов отсутствуют, векторная модель сигнала ВП значительно упрощается:
,
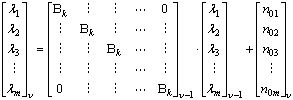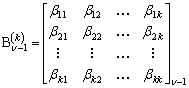, (3)
здесь k - количество каналов на одном пациенте, m=k2. В этом случае количество неизвестных параметров векторной модели ВП уменьшается до (m+m). В процессе решения задачи определения параметров векторной модели ВП человека, была получена формула, однозначно определяющая матрицу коэффициентов 
по известной матрице формирующего шума . В данной модели сигнала (3), параметры были оптимизированы по критерию
.
Разработанный алгоритм определения параметров векторной модели сигнала ВП был реализован в среде программирования Delphi 7. Используя реализации сигналов ВП, на основе результатов работы программы была построена модель сигнала ВП человека. Полученная модель может быть использована в векторной нестационарной фильтрации для повышения достоверности выделяемого сигнала ВП. Применение векторной нестационарной фильтрации для выделения ВП человека имеет значительные преимущества перед методом когерентного усреднения в плане повышения качества выделяемого сигнала и увеличения скорости выделения.