Рассмотрены вопросы определения функции зависимости многомерного признакового пространства при решении задач классификации. Вводится понятие эталонного состояния признака, в котором он не поддается влиянию других признаков. Предлагается процедура определения функции зависимости признаков, имеющих эталонное состояние.
В задачах многомерной классификации объектов признаковое пространство может быть достаточно сложным для его использования без предварительной обработки. Такая сложность, как правило, обусловлена тем, что признаки измерены в разных шкалах, часть признаков неинформативна или признаки зависимы, т.е. для признаков 
существует функция 
, такая что:
, 
; 
,
где М - размерность признакового пространства.
Задача классификации еще более усложнится, если предположить, что часть признаков характеризуется эталонным состоянием, в котором они условно не влияют друг на друга. То есть существует порог влияния группы признаков на признак xi такой что 
, причем признаки могут принимать значение отличное от Null.
Таким образом, каждый признак объекта, зависящий от других признаков, имеет матрицу состояний 
, где 
- эталонное состояние (минимальное значение), определяемое отсутствием влияния на признак других признаков; 
- функция зависимости признака; 
- максимальное значение признака, которое можно достичь путем изменения других признаков. Причем в эталонном состоянии признак может принимать сколько угодно разных значений. Функция зависимости может быть получена двумя способами: 1. Задана экспертно; 2. Получена с помощью аппарата математической статистики на основе ряда наблюдений.
В этом случае признаковое пространство 
состоит их трех подпространств: 
- подпространство признаков, независимых от других признаков; 
- подпространство признаков, зависимых от других, не имеющих эталонного состояния в котором они условно не зависят от других признаков или не оказывают влияния на другие признаки; 
- подпространство признаков, зависимых от других, имеющих эталонное состояние в котором они условно не зависят от других признаков или не оказывают влияния на другие признаки, где 
, М - размерность признакового пространства.
Тогда полное признаковое пространство определяется объединением своих подпространств:
Функция зависимости, в общем случае, может быть построена на основе множественной регрессии. Однако характер зависимости в каждом конкретном случае должен определяться исходя из специфики задачи.
Рассмотрим случай линейной регрессии.
1. Подпространство признаков, зависимых от других, не имеющих эталонного состояния, в котором они условно не зависят от других признаков или не оказывают влияния на другие признаки.
Функция, описывающая зависимость признака xi от набора признаков 
выглядит следующим образом:
(1)
Для определения параметров уравнения множественной регрессии перейдем к уравнению регрессии в стандартизированном масштабе:
, (2)
где 
, стандартизованные переменные:
, 
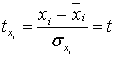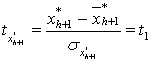
где 
- среднее значение признака, 
- среднеквадратическое отклонение, для которых среднее значение равно нулю: 
, а среднее квадратическое отклонение равно единице: 
; β - стандартизированные коэффициенты.
Оценить параметры стандартизированного уравнения регрессии можно с помощью метода наименьших квадратов (НМК). При его применении строится система нормальных уравнений вида:
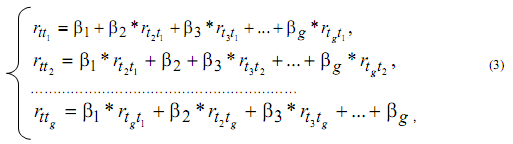
где r - линейные коэффициенты парной корреляции.
Система уравнений решается с помощью метода определителей:
,
где 
- определитель системы, 
- частные определители, получаемые путем замены соответствующего столбца матрицы определителя системы данными левой части системы.
(4)
Вычисленные таким образом коэффициенты регрессии 
можно сравнить друг с другом и определить степень влияния отдельных признаков на зависимый параметр.
Далее переход от уравнения в стандартизированном масштабе к уравнению в натуральном масштабе осуществляется путем вычисления коэффициентов 
по следующей формуле.
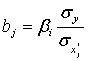, (5)
где 
; 
.
Параметр а определяется исходя из следующего соотношения:
2. Подпространство признаков, зависимых от других, имеющих эталонное состояние в котором они условно не зависят от других признаков или не оказывают влияния на другие признаки.
Функция, описывающая зависимость признака xi от набора признаков 
выглядит, как и в предыдущем случае, с некоторыми дополнениями:
,
где 
если 
и 
если 
; 
; 
- порог влияния признака 
на признак xi.
Решение линейного уравнения множественной регрессии происходит аналогичным способом, путем преобразования его к стандартизированному виду, применению метода наименьших квадратов и последующим нахождением коэффициентов нормального уравнения.
Таким образом, используя метод стандартизированных уравнений множественной регрессии можно выбрать оптимальный вариант факторов, включенных в модель, поскольку факторы с наименьшим значением βi имеют наименьшую степень влияния на зависимый параметр и могут быть исключены.
СПИСОК ЛИТЕРАТУРЫ
- Елисеева И.И., Курышева С.В., Костеева Т.В. Эконометрика - М.: Финансы и статистика, 2003.
- Елисеева И.И, Юзбашев М.М. Общая теория статистики - М.: Финансы и статистика, 2001.
- Загоруйко Н.Г. Прикладные методы анализа данных и знаний.- Новосибирск: Институт математики, 1999.