Эффективность использования неспециализированного гетерогенного кластера напрямую зависит от умения учитывать и планировать его нагрузку. Повысить точность прогнозирования времени выполнения задач позволяют стохастические методы оценки времени их выполнения. В качестве математической основы для такой оценки предлагается применение GERT-сетей.
При использовании гетерогенных неспециализированных кластерных систем с невысокой надежностью узлов, как правило, используются библиотеки типа Condor (http://www.cs.wisc.edu/condor/). В частности, Condor позволяет использовать в составе единого кластера узлы, не только различающиеся в аппаратной части, но и работающие под разными операционными системами. Библиотека Condor позволяет использовать для вычислений существующую компьютерную технику и уже имеющиеся коммуникации, тем самым существенно удешевляя стоимость создания кластера. [1]
В данной статье мы рассмотрим вариант организации параллельных вычислений для алгоритма перемножения двух матриц размерности NхN на K процессорах на небольшом кластере, работающем с использованием библиотеки Condor. В качестве способа распараллеливания алгоритма перемножения будем делить вторую матрицу на полосы для каждого из узлов. В качестве аппаратной реализации кластера рассмотрим два варианта: с последовательной и параллельной архитектурой обмена данными. В первом случае узлы получают задание по очереди, друг за другом, тогда как во втором - одновременно. И в том и другом случае кластер обладает одним управляющим узлом (УУ) и несколькими вычисляющими (Уn).
Детерминированные методы оценки времени выполнения подобных алгоритмов можно посмотреть в источниках [2, 3, 4, 7].
В данной работе представлен стохастический метод оценки времени выполнения задачи. Для простоты расчетов, будем считать, что вычислительная система состоит из одинаковых узлов, хотя данный метод легко переносится на гетерогенный кластер.
Для оценки будем использовать стохастические GERT-сети [5, 6]. Под стохастической сетью будем понимать ориентированный граф G=(N, A) с узлами определенного типа. Узлы стохастической сети могут быть интерпретированы как состояния системы, а дуги - как переходы из одного состояния в другое.
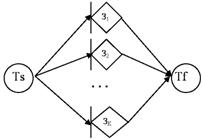
Рассмотрим стохастическую схему выполнения вычислений, где каждая задача Зi вычисляется на отдельном узле.
|
|
|
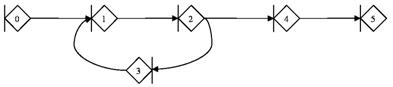
Номер узла графа соответствуют состояниям узла кластера, а дуги - действиям (см. таблицу ниже 1).
Таблица 1. Номер узла графа соответствуют состояниям узла кластера, а дуги - действиям
|
Действие |
Описание |
|
<0, 1> |
Ожидание в очереди |
|
<1, 2> |
Получения данных с УУ |
|
<2, 4> |
Выполнение вычислений, завершившихся успехом |
|
<4, 5> |
Возврат данных |
|
<2, 3> |
Ошибка в ходе выполнения вычислений |
|
<3, 1> |
Устранение сбоя или перенос задачи на другой узел |
Для каждого действия укажем функцию распределения времени выполнения и вероятность выполнения перехода.
Проведя оценку параметров применительно к задаче перемножения двух больших матриц для кластера, организованного в классе общего доступа университета (где время непрерывной работы узла в среднем было принято около 12 часов), получим следующие результаты:
- При условии достаточности доступных ресурсов, возможности умеренного распараллеливания задачи и небольшого (сопоставимого со временем доступности узлов) времени вычисления каждой из подзадач на узле, использование подобных систем вполне оправдано.
- Разница в стохастической и детерминированной оценках времени вычислений уменьшается с уменьшением времени, необходимого для выполнения конкретной задачи на каждом из узлов.
- Для параллельной архитектуры существует максимум коэффициента эффективности использования узлов, а для последовательной еще и максимум коэффициента ускорения.
СПИСОК ЛИТЕРАТУРЫ
- Douglas Thain, Todd Tannenbaum, and Miron Livny. Distributed Computing in Practice: The Condor Experience. Computer Sciences Department, University of Wisconsin-Madison. 2004.
- Букатов А.А., Дацюк В.Н., Жегуло А.И. Программирование многопроцессорных вычислительных систем. Ростов - на - Дону. Издательство ООО «ЦВВР», 2003. ISBN 5-94153-062-5. c. 40-48.
- Шпаковкий Г.И. Серикова Н.В. Программирование для многопроцессорных систем в стандарте MPI. - Минск, БГУ, 2002. - c.12-13, 235-240.
- Yuan Shi. Reevaluating Amdahl´s Law and Gustafson´s Law. http:// http://www.cis/. temple. Edu /~shi/docs/amdahl/amdahl.htm
- Филлипс Д., Гарсиа-Диас А. Методы анализа сетей.-М.: Мир, 1984.
- K. Neumann. Stochastic Project Networks. Temporal Analysis, Scheduling and Cost Minimization. Springer-Verlag. p. 37-115.
- Письман Д.М. Модели оценки времени выполнения задачи на кластере с последовательной и параллельной архитектурой обмена данными. Вестник университетского комплекса. Красноярск: ВСФ РГУИТП, НИИ СУВПТ. 2005.- Вып. 3 (17). с. 161-175.