В работе численно решаются уравнение Пуассона для потенциала в окрестности пылевой частицы при больцмановском распределением концентрации электронов и моделирование ионного потока на нее методом молекулярной динамики. Вокруг частицы выделяется элементарная сферическая ячейка с радиусом, определяемом концентрацией пылевых частиц 
. Ионный поток формируется за счет ионизации газа электронами внутри ячейки с частотой Z ne, где Z - частота ионизации, производимая одним электроном, определяемая скоростью ухода ионов на пылевую частицу, 
- концентрация электронов.
Уравнение Пуассона решалось на каждом временном интервале Δt на одномерной сетке с шагом по радиусу h при нулевых значениях потенциала и его градиента на границе ячейки r=rd
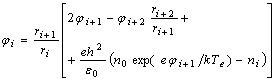(1)
Потенциал пылевой частицы определялся в процессе решения при достижении радиуса частицы r=a.Начальное распределение потенциала может быть произвольным. Для уменьшения количества шагов по времени оно задавалось близкое к реальному по аппроксимирующей формуле:
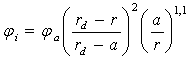(2)
Начальная концентрация ионов определялась по (1). Ионы объединялись в крупные частицы числом 200 на интервале h с равномерным распределением по длине интервала. Через каждый интервал времени t0=4·10-3(wi)-1 (wi - ионная плазменная частота) в каждом интервале h рождалось новая крупная частица с зарядом 
и равномерным случайным расположением по интервалу h. Абсолютная скорость новой частицы и ее угол с радиусом разыгрывались в соответствии с максвелловским распределением с температурой атомов «T». Через время от рождения обратное частоте ион-атомовых столкновений τ=1/νi разыгрывание скорости иона производилось заново. При достижении радиуса пылевой частицы ион поглощается.
Частота ионизации Z корректировалась на каждом временном шаге для компенсации ухода ионов на пылевую частицу. Движение крупных частиц моделировалось в соответствие с уравнением
(3),
где индекс нуль соответствует значениям при рождении частицы. Число одновременно находящихся в ячейке крупных частиц достигало 2·106. На рисунке приведено распределение потенциала по радиусу при a=0,02·λd, rd=0,6·λd (λd - дебаевский электронный радиус). Видно существенное влияние температуры ионов и столкновений даже при малых их значениях.
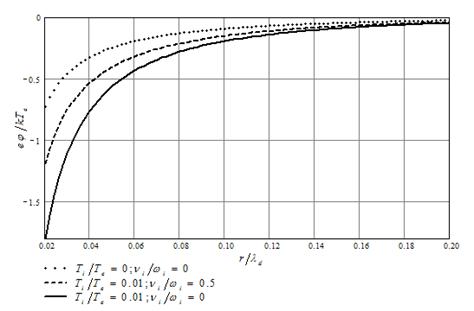
Рисунок 1. Распределение потенциала по радиусу при a=0,02·λd, rd=0,6·λd
Работа выполнена в рамках проекта PZ-013-02, поддерживаемого совместно Американским фондом гражданских исследований и развития (АФГИР), Министерством образования РФ и правительством Республики Карелия.