Наличие в задаче неизвестной границы приводит к большим трудностям, связанными с учетом изменения параметров задачи, для определения которых необходимо знать полную геометрию границ области. В связи с этим, в качестве первого приближения в теоретическом анализе процесса ЭХРО используется модель идеального процесса. Согласно этой модели, для условий ЭХРО постоянным током, электрическое поле в межэлектродном промежутке можно считать потенциальным, т.е. 
где 
- вектор напряженности электрического поля, 
- потенциал электрического поля. В идеальном процессе ЭХРО электрическое поле может быть описано уравнением Лапласа 
. Значения потенциала 
, 
на поверхности анода и катода величины постоянные.
В стационарном режиме форма обрабатываемой поверхности в подвижной системе координат, связанной с катодом, не изменяется. Это означает, что поверхность анода перемещается вместе с катодом с постоянной скоростью 
. В этом случае линейная скорость анодного растворения 
по нормали к поверхности анода в любой точке анода будет равна:
(1)
где 
угол между вектором скорости 
подачи катода и единичным вектором 
внешней нормали к аноду.
При постановке и решении задач ЭХРО используется гидродинамическая аналогия электрического поля, согласно которой плоское потенциальное электрическое поле моделируется фиктивным течением идеальной несжимаемой жидкости. При этом потенциалу поля ставиться в соответствие функция тока фиктивного течения, силовой линии электрического поля - эквипотенциальная линия. Если ввести комплексный потенциал электростатического поля 
, где 
безразмерный потенциал электрического поля, то вдоль линии 
имеем 
, где, в случае гидродинамической интерпретации задач ЭХРО, 
- вектор скорости фиктивного потока идеальной несжимаемой жидкости. Угол наклона скорости к оси абсцисс с точностью до знака совпадает с углом . Тогда условие (1) имеет вид
(2)
и определяет годограф скорости указанного течения на неизвестной анодной границе, здесь 
- постоянные коэффициенты [1]. Гидродинамическая аналогия облегчает формулировку краевых задач теории ЭХРО и позволяет применять методы расчета, разработанные при решении задач гидродинамики.
Рассматривается плоская задача теории электрохимической размерной обработки металлов, состоящая в нахождении формы анодной границы, при электрохимической размерной обработке металлов полигональным катодом в установившемся режиме. Для решения задачи вводится прямоугольная система координат 
, связанная с катодом-инструментом и считается, что движение катода осуществляется в направлении оси ординат.
В односвязной области плоскости 
рассмотрим фиктивное течение идеальной жидкости, ограниченное твердой полигональной стенкой, соответствующей границе катода 
, и свободной поверхностью, соответствующей анодной границе.
Пусть в плоскости вспомогательного комплексного переменного 
области течения конформно соответствует область 
, причем свободной поверхности соответствует дуга окружности 
. Будем искать функцию 
, конформно отображающую область 
на область течения, причем точкам 
на полигоне, в которых скачком меняется направление вектора скорости, соответствуют точки 
. Чтобы построить , достаточно найти производную комплексного потенциала 
в плоскости вспомогательной переменной 
и функцию Жуковского
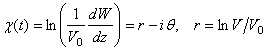, где V - модуль скорости фиктивного течения, 
- значение V на бесконечности в точке А, - угол наклона вектора скорости к оси 
, который равен (с точностью до знака) углу между вектором скорости подачи катода и вектором внешней нормали к аноду. На свободной поверхности из условия (2) получим граничное условие, связывающее вещественную и мнимую части функции 
(3)
Будем искать функцию 
в виде суммы 
, где 
- функция Жуковского для течения по той же схеме, но с условием 
на аноде, а 
- аналитическая в и непрерывная в 
функция.
Функцию , дающую решение краевой задачи можно представить в виде ряда 
, где 
- вещественные постоянные, множитель введен для учета граничного условия 
.
В частном случае при обработке двугранным катодом-инструментом, функции 
и 
имеют следующий вид
. 
Для численного решения задачи задаются геометрические параметры 
,параметры характеризующие свойства электролита. Численные расчеты формы обрабатываемой границы для этого частного случая проведены при следующих значениях параметров:
.1) - a=-0.301, b=2.401; 2) - a=-0.205, b=1.865; 3) - a=0.21, b=1.28; 4) - a=-0.127, b=1.467; 5) - a=0.141, b=1.104; 6) - a=0.077, b=0.931.
Список литературы
- Котляр Л.М., Миназетдинов Н.М. Определение формы анода с учетом свойств электролита в задачах электрохимической размерной обработки металлов. //Прикладная механика и техническая физика, 2003, Т. 44, №3, С. 179-184