Целью работы является обоснование правомерности применения верхних оценок фундаментального решения известного оператора к фундаментальному решению оператора, порожденного естественной нормировкой пространств Соболева.
1. Естественная норма в пространстве Соболева. Объектом нашего внимания будут пространства Соболева 
, состоящие из функций, заданных на множестве Rn, и 
, состоящие из периодических функций с единичной матрицей периодов. В последнем случае в качестве фундаментальной области выступает единичный куб с отождествленными противоположными гранями 
: 
. Норма в этих пространствах будет задана в виде
(1)
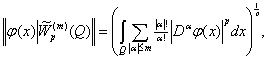(2)
в обеих формулах 
. Предельные значения показателя суммируемости индуцируют новые пространства. При p=1 выражения (1) и (2) изменятся очевидным образом
(3)
(4)
В эти пространства объединяются функции, обобщенные частные производные которых суммируемы в Rn или в Q.
Выписывание естественных норм в 
и 
предварит следующее утверждение.
Теорема 1. Для любого конечного числа измеримых существенно ограниченных в совокупности на Rn функций fk, таких, что |fk|p суммируемы при всех достаточно больших p и
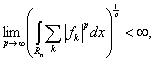
выполняется равенство
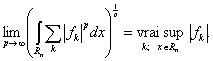(5)
Замечание. Условие существования конечного предела при 
в случае интегрирования по Rn или любой неограниченной области 
предполагает исключение из рассматриваемого класса таких функций, как 
, 
и других, для которых несобственный интеграл расходится. Если же интегрирование происходит по ограниченной области , то для таких функций утверждение теоремы остается справедливым.
Доказательство теоремы 1. Здесь будет использована идея из [1], примененная там для вывода нормы функции в пространстве 
. С учетом обозначения 
можно построить неравенство
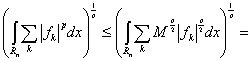
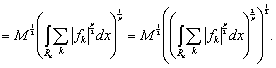(6)
Интеграл справа с показателем 
мало отличается от интеграла с показателем p при больших значениях этого показателя, а потому
(7)
откуда следует, что
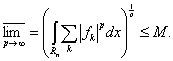(8)
По определению существенного максимума как верхней грани числового множества для любого положительного ε, не превосходящего M, существуют значения fk, удовлетворяющие неравенству 
, причем для выполнения последнего необходимо существование ограниченного множества 
ненулевой меры, в каждой точке которого определены указанные значения. Так как 
, можно записать обратное неравенство
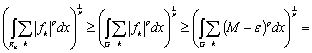
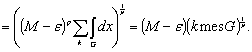(9)
Операция взятия нижнего предела приводит к неравенству
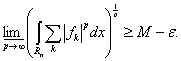(10)
С учетом произвольности ε из (8) и (10) следует утверждение теоремы.
Таким образом, для (1) и (2) предельными при p→∞ будут нормы
(11)
(12)
Эти пространства будут включать в себя функции, существенно ограниченные в Rn или, соответственно, в Q со своими обобщенными частными производными.
Поскольку излагаемые факты нацелены на применение в области кубатурных формул, то следует оговорить условие, при котором они имеют смысл. Кубатурная сумма, приближающая интеграл, представляет собой с точки зрения функционала линейную комбинацию дельта-функций δ(x), которые имеют смысл при воздействии на непрерывные пробные функции, отсюда требование вложения основного пространства в пространство непрерывных функций 
, что выражается неравенством mp>n (n - размерность Rn) [2].
2. Фундаментальное решение вспомогательного оператора. В качестве такового будет использован оператор
(14)
порожденный нормой, введенной в [3]
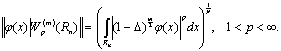(15)
В этих двух формулах Δ - оператор Лапласа.
Не приводя вида фундаментального решения G(|x|) оператора (14) и его оценок по множествам |x|<1 и |x|>1, укажем источник их получения [1]. Оценки производных 
послужат основой доказательства всех наших утверждений. В теоремах 2-4 фигурируют функции, заданные на всем Rn.
Теорема 2. Фундаментальное решение G(|x|) оператора (14) принадлежит пространству 
, где 
, 
, pm>n.
Доказательство. Для начала потребуется рассмотрение 
-норм производных при
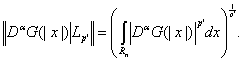(16)
Интеграл из (16) удобнее разбить на сумму
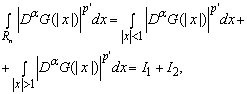(17)
после чего оценить каждое из слагаемых
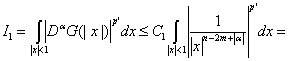
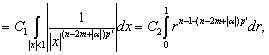(18)
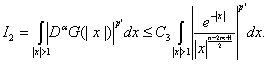(19)
В последнем равенстве (18) совершен переход к сферическим координатам. Максимально возможный порядок производной равен m, а потому
(20)
Интеграл справа существует, если (n-m)p´<n, т.е.
(21)
Сходимость несобственного интеграла в правой части (19) очевидна. Из (19), (20), (21) следует, что при mp>n 
, 
, т.е. 
, . Что касается предельных значений, то если 
, 
, тогда неравенства (18) и (19) выполняются. Если же p=1, p´=∞, то требуется доказать существенную ограниченность , на Rn. При любом 
выполняются неравенства
если 
(22)
в том числе и при 
, а также
(23)
Правая часть (23) имеет глобальный максимум в тех точках, где 
, а следовательно, 
- ограничена. Теорема доказана.
3. Фундаментальное решение оператора, порожденного естественной нормой. Норма (1) порождает оператор
(24)
где Δ - оператор Лапласа. Фундаментальное решение его 
как обобщенную функцию, действующую на основные функции из 1<p< ∞, можно получить в виде несобственного интеграла, если применить к уравнению
(25)
прямое и обратное преобразования Фурье
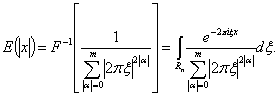(26)
Здесь 
Теорема 3. Функция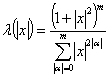 
, 
, является множителем Марцинкевича при 1<p< ∞.
Доказательство. Как функция n действительных переменных 
, где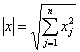 
, является отношением многочленов равных степеней. Знаменатель ее не имеет действительных корней, и потому непрерывна на Rn. Так как 
, то ограничена. Производные 
, где 
также непрерывны и 
, откуда следует ограниченность произведения, стоящего под знаком предела. Таким образом, выполнены условия теоремы 1.5.4 [1], что доказывает наше утверждение.
Теорема 4. Оценки для справедливы и для 
, , .
Доказательство. Согласно определению [1], если λ - множитель Марцинкевича, то при 1<p<∞ выполняется неравенство
(27)
где 
, 
- константа, зависящая от p´. Функции 
и 
связаны выражением
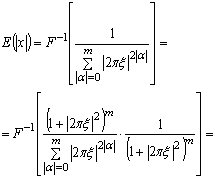
(28)
Последнее равенство на основании теоремы 3 вытекает из свойств множителя Марцинкевича [1]. Поскольку по правилу дифференцирования свертки 
, , то
(29)
Интеграл справа, определяющий норму, существует при pm>n. Отсюда непосредственно следует утверждение теоремы для 
. Однако, тот же интеграл существует и при p=∞. Достаточно применить предельный переход к неравенствам (18) и (19), оценивающим его. Здесь, кроме того, отпадает необходимость в ограничениях на m и n. В случае же p=1 существенная ограниченность следует из существенной ограниченности , . Теорема доказана.
Из теоремы 4 непосредственно следует принадлежность фундаментального решения оператора, порожденного естественной нормой, пространству 
в условиях теоремы 2.
СПИСОК ЛИТЕРАТУРЫ
- Никольский С.М. Приближение функций многих переменных и теоремы вложения. - М.: Наука, 1977. - 456 с.
- Соболев С.Л. Введение в теорию кубатурных формул. - М.: Наука, 1974. - 808 с.
- Шойнжуров Ц.Б. Теория кубатурных формул в функциональных пространствах с нормой, зависящей от функции и ее производных: Дис. ... докт. физ.-мат. наук (01.01.01, 01.01.07) / Вост.-Сиб. технол. ин-т. - Улан-Удэ, 1977. - 235 с.