Основная тенденция современной нефтепереработки и нефтехимии - создание крупнотоннажных, энергоэффективных и комбинированных установок на базе агрегатов большой единичной мощности. Для реализации тепловых процессов в нефтеперерабатывающей промышленности широкое распространение получили трубчатые печи. В зависимости от специфики технологического процесса, физико-химических свойств нагреваемой среды и вида топлива, применяют печи различных конструкций и параметров. Неизменно актуальным остается требование повышения энергоэффективности и экологической безопасности производственного процесса, учитывая его высокую энергоемкость. Вместе с тем, габаритные размеры трубчатых печей и другие конструктивные особенности не позволяют в полной мере осуществить совершенствование их конструкций на базе экспериментальных исследований. В этой связи на первый план выходят задачи разработки расчетных методов.
В данной работе в качестве объекта исследования выбраны трубчатые печи типа ГН. Печи ГН работают следующим образом. Факел, образованный при сжигании топлива, под углом с двух сторон настилается на стену, расположенную в центре печи. Тепло от раскаленной стены и факела передается радиантным экранам, после чего газы сгорания поступают в камеру конвекции, отдавая тепло трубам конвективного змеевика, и через газосборник и трубу уходят в атмосферу.
Необходимость совершенствования теплотехнологий, широкое внедрение процессорных методов контроля и управления ставят в число приоритетных задач более детальную разработку физико - математических моделей гидродинамических, тепло- и массообменных и термодинамических процессов. В случае математического моделирования этих явлений и реализации численными или аналитическими методами, получаемые результаты обладают большей общностью и удобством для практического использования - результат, представленный простой формулой, предпочтительнее машинного решения, особенно когда найденная зависимость является промежуточным звеном исследования сложного явления (реконструкция поля температур в анализе теплообмена, решения задач оптимального управления теплотехнологическими процессами и т.п.).
Учитывая вышеизложенное, в работе обосновывается важность решения задач управления с целью оптимизации анализируемых конструкций и устройств трубчатых печей, как объекта с распределенными параметрами. Для решения задачи оптимального управления предлагается в достаточно общем виде следующая математическая модель и соответствующая краевая задача.
При исследовании процесса горения капель жидкого топлива в воздухе в основном представляет интерес распределение концентраций компонентов в камере печи при статических и динамических режимах работы. Исходя из одномерности движения потоков, математическая модель нестационарного горения может быть представлена следующими уравнениями:
1. Уравнение неразрывности
, (1)
где ρ- массовая плотность смеси; 
- скорость движения смеси. Для покомпонентной модели процесса горения уравнение (1) можно записать в виде
, (2)
здесь 
- линейный размер; x - концентрация горючего вещества в смеси (
); 
- время сгорания;
2. Уравнение движения в виде
, (3)
3. Уравнение сохранения энергии
, (4)
где q - теплота сгорания топлива; Q (T)- потери на излучение; S - энтропия, причем 
( 
, т.к. для жидкостей различие между 
и 
незначительно; Θ - температура сырья (нефтепродукта в радиантных трубопроводах печи); K1 - коэффициент теплопередачи для рабочего потока.
(5)
4. Уравнение теплообмена в виде
, (6)
где K2 - коэффициент теплопередачи для стенки печи.
Уравнения (1) - (6) представляют собой математическую модель теплового процесса печи, которая может быть реализована относительно скорости движения смеси и концентрации горючего вещества в смеси по длине камеры сгорания, а также может быть использована для получения других параметров печи, которые зависят от x и u.
Для получения x и u как функции длины в камере сгорания формулируется краевая задача типа Коши, к уравнениям (1) - (6) добавляют начальные условия:
; 
(7)
и граничные условия, которые имеют вид:
.(8)
В качестве управляющих параметров приняты изменения горючей смеси по концентрации, скорости и температуре во входном потоке и соответствующие управления имеют вид:
; 
; 
. (9)
Критерий оптимальности в этом случае будет равен минимуму отклонения температуры потока от заданной:
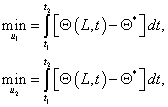(10)
где 
- задаваемая величина температуры сырья.
Выводы
- Реализация математической модели позволяет построить алгоритм оптимального управления режимами работы технологических печей в нефтеперерабатывающей промышленности.
- Полученные результаты могут быть использованы для оптимального управления работой теплотехнологических агрегатов непрерывного действия с промежуточным теплоносителем.
- Выявлено влияние концентрации капель жидкого топлива на скорость распространения пламени на начальной стадии процесса. Установлено что по мере увеличения концентрации капель жидкого горючего скорость распространения пламени уменьшается при и несколько возрастает при более высоких . При очень малых и очень больших концентрациях горючего, влияние капель по существу отсутствует. При увеличении количества сконденсированного горючего полная концентрация, при которой достигается максимальная скорость распространения пламени, сдвигается в сторону больших значений концентрации горючего, а значение максимальной скорости распространения пламени уменьшается. Влияние концентрации жидких капель на скорость горения идентично влиянию концентрации жидких капель на скорость распространения пламени, причем этот эффект выражен тем сильнее, чем выше скорость распространения пламени. А это указывает на то, что в случае с высокой скоростью распространения пламени жидкие капли размером 1 мкм не успевают полностью испариться перед фронтом пламени.
- Для уравнений (1) - (10) получены необходимые условия оптимальности, которые используются для определения оптимальных управлений. Соответствующая сопряженная краевая задача по структуре аналогична описанной задаче и отличается от последней заданием начальных условий в момент времени .