Наблюдения показывают, что одной из причин повреждения зерна в пружинном транспортере оказывается дробление его между кожухом и пружиной при поперечных колебаниях последней. Особенную опасность представляют резонансные колебания пружины, которые могут возникнуть при определенных критических скоростях ее вращения. В связи с этим возникла необходимость расчета жесткости пружины, так как характеристики жесткости входят в дифференциальные уравнения колебательного движения.
Для расчета колебаний пружины можно воспользоваться основным дифференциальным уравнением движения в поперечном направлении. Дифференциальное уравнение поперечных колебаний пружины получим из рассмотрения условий динамического равновесия элемента dx выделенного из произвольно закрепленной пружины. Проектируя все силы, действующие на рассматриваемый элемент (включая в соответствии с принципом Даламбера силы инерции) на вертикальную ось y , будем иметь 
откуда
(1)
где Q - поперечная сила; q1 - интенсивность сил инерции массы
, (2)
( F- площадь поперечного сечения; ρ - плотность материала; y - поперечное перемещение; t - время).
Подставив (2) в (1). найдем уравнение поступательного движения элемента колеблющегося стержня:
. (3).
Простейшим периодическим решением уравнения (4) является так называемое главное колебание, в котором функция прогиба колеблющегося стержня изменяется с течением времени по гармоническому закону
(4)
Функция φ(x) , устанавливающая закон распределения максимальных отклонений точек оси стержня, называется формой главного колебания или собственной формой.
Для получения уравнений собственных форм получим
, где 
Общее решение уравнения имеет вид
, (5)
Здесь А, В, С, D (постоянные интегрирования, определяемые из условий закрепления стержня. Так, например, для шарнирно-закрепленного стержня (рис. 2.68) условия на концах будут:
при 
при 
Из полученного частотного уравнения находим: 
Из равенства 
определим собственную круговую частоту: 
период 
и частоту колебаний, гц, 
Общее решение дифференциального уравнения (2.160) применительно к рассматриваемой балке на двух опорах может быть записано в виде
, (6)
где a1 и b1 должны быть подобраны из начальных условий (при t=0).
Решение этого уравнения применительно к пружине, свободно лежащей на двух опорах с расстоянием, L - между ними, дает значения критической частоты ω и критической скорости вращения Nkp.
Значение момента инерции J , входящее в приведенные формулы может быть найдено по методу Тимошенко, исходя из энергии, накапливаемой в витках при их изгибе в продольной плоскости (данный метод был разработан для определения жесткости на поперечный изгиб витых пружин).
При анализе изгиба такого тела рассматривают отдельно энергию от составляющей момента в плоскости витка и в нормальной к ней плоскости. Суммарная энергия упругой деформации витков пружины составляет:
где M - изгибающий момент; n - число шагов витков пружины в пределах изучаемого участка; α - угол наклона винтовой линии; b - толщина витка; d - его ширина; R - средний радиус пружины; G - модуль сдвига; ρk - средний радиус кривизны витка, определяемый как 
; ε - смешение нейтральной оси при изгибе витка шнека, определяемое из уравнения 
, где ρ i и ρ 0 - соответственно внутренний и наружный радиусы транспортера.
От величины накопленной энергии можно перейти к характеристике жесткости, приравняв:
, ( ρ c - радиус кривизны в плоскости изгиба).
Отсюда приведенная характеристика жесткости витков пружины оказывается равной:
(7)
Входящий в уравнение коэффициент k отражает связь витков пружины с ее корпусом. При малой связи, как в нашем случае с большим шагом, этот коэффициент может быть принят равным единице, с увеличением связи коэффициент увеличивается.
Программа расчета характеристик транспортеров для выбранных значений параметров и зависимость критической скорости вращения от длины пружины приводится на рисунке 1.
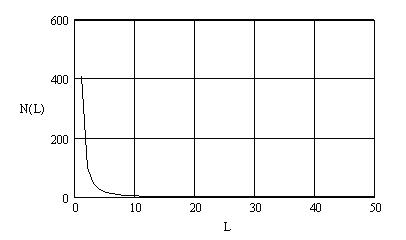
Рис. 1. Зависимость критической скорости вращения от длины пружины.
Расчет характеристик по параметрам реальных транспортеров зернопогрузчиков показывает, что колебания в транспортере определяются в основном жесткостью его пружины. Аналогичные результаты получены исследованиями распределения напряжений в различных точках транспортера, проведенные с применением фотоупругих моделей для шнека.
Диапазон значений частот колебания транспортеров в зависимости от их длины представляет некоторую область, в центре которой лежит кривая расчетных значений согласно приведенному уравнению. С увеличением длины транспортера критическая скорость вращения, отвечающая резонансным колебаниям, резко уменьшается. Критическая скорость уменьшается с увеличением угла наклона транспортера. При величине угла наклона менее 30° критическая скорость изменяется мало и соответствует расчетной формуле, с превышением этого угла критическая скорость возрастает по затухающей криволинейной зависимости.
Колебания транспортера в известной мере гасятся сыпучей массой, находящейся внутри его кожуха. Чем больше коэффициент заполнения шнека, тем меньше критическая скорость его вращения. Влияние коэффициента заполнения проявляется в одинаковой мере при всех значениях угла наклона транспортера.