Нами в работе [1] проводилось численное решение уравнения Пуассона (1), представленного аналогично Ленгмюру в виде уравнения "плазма-слой", с частными аналитическими решениями на границе ячейки Зейтца-Вигнера и тонких сеточных слоях в промежутке.
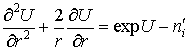(1),
где выражение для концентрации ионов:
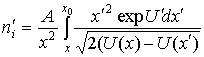(2)
Прямое решение уравнения Пуассона, возможное при нулевой температуре ионов, затруднено при большой области возмущения 
и, соответственно, малой частоте объемной ионизации. Тогда вблизи границы области возмущения 
; 
. Знаменатель в (2) близок к нулю и ошибки вычисления приводят к неустойчивостям.
В методе молекулярной динамики ионный состав плазмы заменяется крупными ионными частицами общим числом от одного до несколько миллионов. При такой замене увеличивается пропорционально заряд и масса модельных частиц, при сохранении их отношения q/m. При этом не изменяются уравнения движения и, соответственно, их решения. Значения заряда и потенциала пылинки, полученные по результатам численного эксперимента, представлены на рисунках 1 и 2. На рисунке 3 показан график зависимости силы, действующей на пылинку от размера ячейки. Моделирование проводилось для плазмы с температурой 
=0,01, параметром здесь является длина свободного пробега макроинов Li. Согласно предложенному нами критерию, если удаленная пылинка приближается к другой, то сила, действующая на частицу, возрастает до максимума, что и видно на рисунке 3, а далее резко уменьшается, что свидетельствует об устойчивой конфигурации системы пылевых частиц в области максимума этой силы.
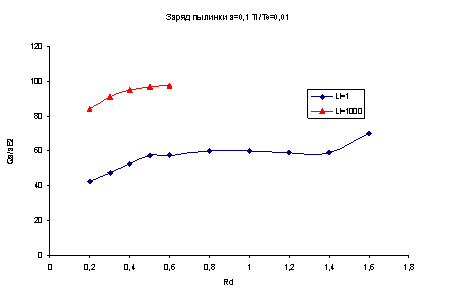
Рис.1
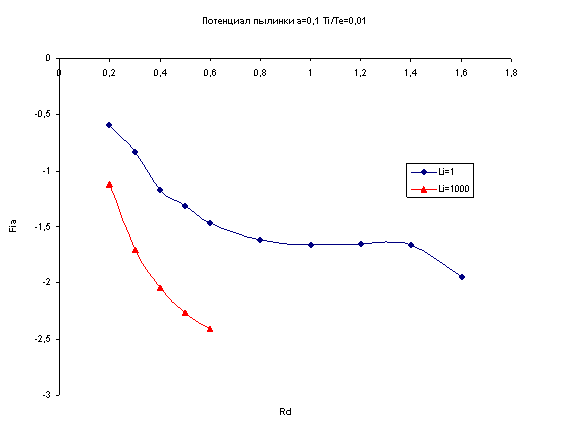
Рис. 2
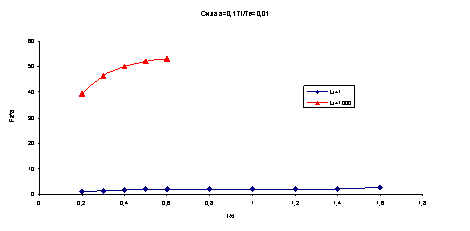
Рис. 3
Исследования, описанные в данной работе, были проведены в рамках проекта PZ-013-02, поддерживаемого совместно Американским фондом гражданских исследований и развития (АФГИР), Министерством образования РФ и правительством Республики Карелия.
СПИСОК ЛИТЕРАТУРЫ:
-
Сысун В.И., Хахаев А.Д., Олещук О.В., Шелестов А.С. Заряд и потенциал пылевой частицы в плазме низкого давления с учётом ионизации в области возмущения // «Физика плазмы» 2005, т.31, №9, с. 834-841