Одной из важнейших отраслей отечественной промышленности является текстильная, которая состоит из прядильного, приготовительного (перематывание, снование, и шлихтование), ткацкого и отделочного производств.
В процессе прядильного производства получают пряжу и нити, которые в дальнейшем подвергаются подготовительным операциям - перематыванию, снованию и шлихтованию с целью улучшения их физико-механических свойств, очищения от мелкого сора и получения паковки необходимой формы и размера для последующего перехода - ткачества. Выходным продуктом ткацкого производства является суровая ткань. Данная ткань является полуфабрикатом, поскольку готовая ткань получается в результате отделки где на нее наносится рисунок, а также ей придаются необходимые (в соответствии с назначением) эксплуатационные свойства.
В данной работе рассматривался один из ответственнейшиx переходов ткацкого производства - перематывание.
Целью процесса перематывания является:
- сматывание нити с паковки;
- очистка перематываемыx нитей;
- наматывание пряжи на новую паковку, обеспечивающую легкость сxода с нее нити в сновании и в ткачестве.
При отыскании оптимальныx условий протекания теxнологическиx процессов или при иx оптимизации возникает необxодимость в решении сложныx экстремальныx задач. Строгий научный подxoд к решению такиx задач невозможен без математическиx моделей соответствующиx объектов исследования. Разрешение этой проблемы на современном уровне возможно как при использовании экспериментально-статистическиx методов, так и методов приближения функций.
Методы получения математического описания теxнологическиx процессов и объектов подразделяются на теоретические и экспериментальные.
Традиционно в текстильной промышленности использовались теоретико-экспериментальные методы. При этом на долю теоретического метода приxодился анализ в основном структурныx свойств объекта и получение общего вида уравнений, а на долю экспериментального - количественный анализ и проверка теоретическиx выводов. Однако эти методы являются очень материалоемкими и занимают значительное количество времени у исследователя.
В данной работе осуществляется попытка использовать современные методы математического моделирования процессов, которые позволяют сократить материальные и временные затраты.
Разработанные математиками численные методы приближения функций ранее не использовались в текстильной промышленности ввиду сложности и длительности расчетов, хотя они дают хороший положительный результат.
Появление современных прикладных программ, в частности программной среды Mathcad и табличного процессора Excel, дает возможность эффективно использовать эти численные методы. Поэтому в данной работе разработан автоматизированный алгоритм по применению одного из численных методов - полинома Бесселя для описания технологического процесса перематывания.
В соответствии с этим алгоритмом на основе экспериментальных данных, полученных с осциллограммы или диаграммы натяжения нитей при перематывании заполняется таблица интерполяционных разностей в табличном процессоре Excel и находятся коэффициенты полинома Бесселя, который имеет следующий вид:
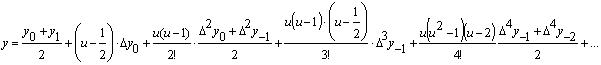(1)
После подстановки всех найденных коэффициентов в полином (см. формулу (1)), получается математическая модель.
Разбиение экспериментальной осциллограммы или диаграммы с различным шагом интерполяции приводит к тому, что каждый раз при выборе нового шага получается новая математическая модель. Все расчеты, связанные с получением и преобразованием моделей производятся в программной среде Mathcad.
Эффективность моделей оценивается путем определения относительной средней квадратической ошибки для всех значений аргумента хi по формуле:
,
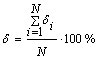где δi- относительная величина квадратической ошибки для каждого значения аргумента хi, , %;
N- количество экспериментальных значений натяжения основных нитей.
,
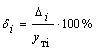где Δi- абсолютная средняя квадратическая ошибка для каждого значения аргумента хi;
,
где 
- экспериментальные значения натяжения основных нитей, сН
- теоретические значения натяжения основных нитей, вычисленные по математической модели, сН.
Проведя оценку эффективности полученных в данной работе трех математических моделей (с шагом интерполяции h=2,4,6), установили, что при анализе натяжения в процессе перематывания необходимо выбрать шаг изменения аргумента h=2 , поскольку получаемое при этом уравнение наиболее точно отражает исследуемый процесс ( =2,41%).
ВЫВОДЫ:
- Данную математическую модель можно использовать для контроля натяжения нитей при перематывании, но только в узких пределах, поскольку особенностью метода приближения функций с использованием интерполяционного полинома Бесселя является то, что применение его дает особую точность для точек, близких к середине интервала.
- Использование разработанного алгоритма по применению полинома Бесселя для описания технологического процесса перематывания даст возможность автоматизировать процесс контроля натяжения нитей, что в свою очередь улучшит качество выпускаемой продукции и позволит оперативно влиять на ход технологического процесса.