Качество тканей во многом определяется натяжением нитей основы и утка в процессе тканеобразования. Причем натяжение нитей основы оказывает большее влияние на физико-механические свойства ткани по сравнению с нитями утка, так как они подвергаются большим силовым воздействиям на ткацком станке.
Изменение натяжения нитей основы за определенный период работы ткацкого станка (например, за один оборот главного вала) можно представить в виде осциллограммы или диаграммы, которые с помощью полинома Чебышева можно преобразовать в математическую модель исследуемого процесса. Применение численных методов для получения математических моделей стало актуальным сравнительно недавно. Раньше из-за отсутствия мощного программного обеспечения, позволяющего производить большое количество вычислений за малый промежуток времени, методы приближения функций не были столь широко распространены, как сейчас. Но даже в настоящее время в текстильной промышленности численные методы практически не используются.
В данной работе по исследованию технологического процесса ткачества осуществляется попытка использования полинома Чебышева для приближенного описания изменения натяжения основы на ткацком станке.
Полученная в результате эксперимента диаграмма изменения натяжения нитей в зависимости от угла поворота главного вала станка обрабатывается в соответствии с разработанным алгоритмом использования полинома Чебышева для контроля натяжения нитей в процессе ткачества.
Проанализировав характер изменения экспериментальной кривой, необходимо перейти к первому этапу обработки диаграммы. Он заключается в том, чтобы из множества существующих функций выбрать ту, которая позволит наилучшим образом аппроксимировать экспериментальные результаты.
Выражение «наилучшим образом» может быть определено критерием наименьших квадратов. Приближение же по Чебышеву определяется условием: как сделать отклонение приближаемой f(x) и приближающей g(x) функций как можно меньшим. Функция g(x), которая является в данном случае полиномом Чебышева P(x), должна быть удобнее в обращении, чем функция f(x).
Далее необходимо выбрать шаг интерполяции и степень полинома. После этого определяется последовательность абсцисс по формуле:
,
где i=0,1,2,...,n
n - степень полинома.
По найденным значениям абсцисс можно легко определить значения аппроксимирующей функции. Теперь искомый полином P(x) может быть написан в виде формулы, дающей интерполяционный полином Лагранжа для абсцисс аi . Достаточно только определить коэффициенты полинома Чебышева bi , которые представляют собой коэффициенты разложения в ряд Фурье.
Подстановка всех найденных коэффициентов в полином Чебышева приводит к получению математической модели.
Эффективность математической модели определяется путем вычисления относительной средней квадратической ошибки для всех значений аргумента хi по формуле:
,
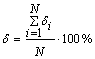где 
- относительная величина квадратической ошибки для каждого значения аргумента хi, , %;
N- количество экспериментальных значений натяжения основных нитей.
,
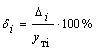где 
- абсолютная средняя квадратическая ошибка для каждого значения аргумента хi;
,
где 
- экспериментальные значения натяжения основных нитей, сН 
- теоретические значения натяжения основных нитей, вычисленные по математической модели, сН.
Предложенный автоматизированный алгоритм по применению полинома Чебышева для описания технологического процесса ткачества позволит автоматизировать процесс контроля натяжения нитей, что в свою очередь улучшит качество выпускаемой продукции и позволит оперативно влиять на ход технологического процесса.