На сегодняшний день существуют два основных механизма распространения реакции: детонация и горение. Скорость распространения фронта детонационной волны определяется скоростью звука в среде и составляет для азидов тяжелых металлов (АТМ) величину ~ 5 км/с. Движение фронта экзотермической реакции горения определяется процессами диффузии и теплопроводности с характерной скоростью ~ 1 м/с.
Скорость распространения реакции взрывного разложения АТМ составляет величину ~ 1 км/с, что в 5 раз меньше скорости детонационной волны и на три порядка больше скорости волны горения. Следовательно, существующие механизмы не могут объяснить наблюдаемую в АТМ скорость распространения реакции.
Предлагаемый новый механизм распространения волны разветвленной цепной реакции по кристаллу АТМ базируется на следующих экспериментально доказанных положениях:
- инициирование взрывного разложения кристаллов АТМ импульсным (~ 20 нс) воздействием является итогом протекания в кристалле разветвленной цепной реакции;
- электронно возбужденные частицы на поверхности кристалла могут безызлучательно передавать свою энергию на достаточно большие (значительно больше постоянной решетки) расстояния с генерацией электронных возбуждений в объеме твердого тела.
Наиболее вероятной моделью взрывного разложения азида серебра (АС), инициированного импульсным излучением, является следующая модель [1]:
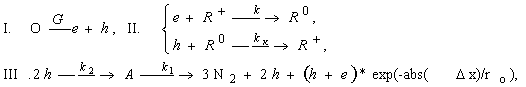
где 
- центры рекомбинации (ЦР) в различных зарядовых состояниях. Первая стадия - генерация e.h. пар внешним излучением. Вторая - рекомбинации e.h. пар на объемных и поверхностных локальных центрах. Третья стадия - взаимодействие двух дырок, локализованных в соседних узлах кристаллической решетки, с образованием промежуточного комплекса А (N6) и последующим его распадом на молекулярный азот (N2) с выделением энергии, идущей на генерацию носителей - стадия развития цепи.Определена скорость распространения цепной реакции по кристаллу в зависимости от констант модели kr, k1, k2.
Аналитически получено выражение для скорости распространения реакции по кристаллу в зависимости от констант модели:
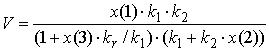, (1)
где х(1), х(2), х(3) - подгоночные параметры, равные соответственно 5.05·1016, 1.87·1019, 2.95.
Скорости реакции, рассчитанные методами численного интегрирования системы дифференциальных уравнений и по формуле (1), отличаются на 1-2% и хорошо согласуются с экспериментом.