Известно, что необходимостью разработки новых подходов к обучению диктуется неудовлетворенностью общества его качеством.
В основе деятельности традиционной системы образования в течение длительного времени лежало представление о разовом характере процесса обучения. Считается, что в ходе обучения человек должен овладеть всей совокупностью знаний, которые могут понадобиться ему в жизни. Однако после резкого ускорения темпов развития общества, стало очевидным и ускорение темпов обновления системы знаний, которое, в свою очередь, сделало актуальной задачу непрерывного обучения человека на протяжении всего периода его активной профессиональной деятельности. Естественно, что в этих условиях происходит переход от «концепции разового образования к образованию многократному, реализующемуся на протяжении всей жизни человека». Необходимо сформировать новый уровень образованности, выработать способности к новым самостоятельным видам деятельности.
Важнейшая цель современной школы - дать личности на любом уровне вузовского образования не только общую и профессиональную подготовку, но и необходимую базу для самообразования, развить способность активно использовать знания для возникающих реальных научных и производственных проблем. Реализация этой цели предполагает, что в современной высшей школе учебный процесс должен приобрести характер самостоятельного и управляемого труда студентов, организуемого и управляемого преподавателем с использованием новейших методов и средств обучения. Кроме того, возникли и активно развиваются новые формы высшего образования, такие как, дистанционное образование, заочное образование на основе «кейс-технологий» и др.
В настоящее время на самостоятельную работу студентов без руководства преподавателя отводится около половины запланированного на изучение предмета времени. Причем количество аудиторных часов, отводимых на математические дисциплины в технических вузах, сокращается. Такое положение требует более эффективного проведения аудиторных занятий и организации самостоятельной работы студентов. Нужно искать такие формы и способы обучения, которые позволяли бы студентам усваивать в отведенное на изучение математики время необходимый объем знаний и умений.
Вместе с тем, в практике высших учебных заведений сложилась такая обстановка, в результате которой самостоятельная работа является одной из наименее организованных и управляемых форм процесса обучения, хотя по важности задач, которые на нее возлагаются, она занимает ведущее место. Это противоречие отрицательно сказывается на результатах процесса обучения в вузах.
Совершенствование высшего технического образования в настоящее время связывают с внедрением новых информационных технологий (НИТ) в учебный процесс. Такой подход основывается на высоких требованиях к уровню информационно-образовательной подготовки современного специалиста. Внедрение современных информационных технологий дает возможность повысить качество обучения, обеспечить уровень мотивации студентов, эффективнее организовать самостоятельную работу, использовать индивидуальный подход в обучении.[1]
Компьютерное обучение, прошедшее в своем развитии несколько этапов, сегодня является неотъемлемой частью учебного процесса высшей школы. В результате накоплен определенный опыт (более 20 лет) внедрения ЭВМ в процесс обучения в высшей школы.
Возникновение новых мощных прикладных программных средств обусловило расширение спектра используемых компьютерных программ. Так, В.В. Шапкин отмечает, что сегодня «обучающие компьютерные программы» можно подразделить на информационные, контролирующие, демонстрационные, иммитационно-моделирующие, программы-тренажеры, справочные, рассчетные [4]. И.П. Половина, объединяя справочные и информационные в справочники для ввода информации по запросу, добавляет к вышеназванным следующие программы: тренажеры для закрепления пройденного материала, генераторы индивидуальных заданий, обучающие программы, развивающие игры (кроссворд и др.). Универсальные обучающие системы (включают в себя целый блок программ) [3].
С возможностью создания вышеописанных компьютерных программ открылись новые перспективы для использования разнообразных методов при обучении высшей математике. Создание методик, ориентированных на самостоятельную работу студентов должно опираться на такие возможности НИТ, как оперативная обратная связь между обучаемым и НИТ, компьютерная визуализация учебной информации, автоматизация процессов вычислительной, информационно-поисковой деятельности, обработка результатов учебного эксперимента с возможностью многократного повторения самого эксперимента, автоматизация процессов информационно-методического обеспечения, организационного управления учебной деятельностью и контроля за результатами усвоения.
Компьютеры позволяют значительно увеличить объем усваиваемой информатизации благодаря тому, что она подается в более обобщенном, систематизированном виде, причем не в статике, а в динамике. Приоритет развивающей функции обучения предусматривает перенос акцентов с увеличения объема информации, предназначенной для усвоения студентам, на формирование умений использовать информацию. Экономия времени за счет сокращения вычислительных операций также позволяет получать больший объем информации, расширить круг задач, включая в процесс обучения и задачи профессиональной направленности.
При обучении математике с использованием НИТ эффективно реализуются важные дидактические принципы, направленные на активизацию познавательной деятельности студентов: индивидуализация и дифференциация процесса обучения (например, за счет возможности поэтапного продвижения к цели по линиям различной степени сложности), осуществление контроля с обратной связью - диагностикой ошибок (констатация причин ошибочных действий обучаемого и предъявление на экране компьютера соответствующих комментариев) по результатам учебной деятельности и оценки учебной деятельности, - осуществление самоконтроля, самокоррекции, тренировки в процессе самостоятельной работы студентов.
Возможность оперативного получения при помощи работы с НИТ, своевременной коррекции учебных действий стимулирует у студентов развитие умений и навыков самостоятельной работы. Это приводит к ускорению темпа обучения, высвобождает время, следовательно, интенсифицирует процесс обучения.
Компьютер как бы соединяет в себе ряд традиционных технических средств обучения, которые всегда использовались, в основном, для усиления наглядности. Компьютер позволяет, например, моделировать ситуации сравнения, аналогии, т.е. преобразует наглядность, делает ее качественно иной. Это активизирует познавательный процесс у обучаемых, развивает мышление (наглядно-действенное, наглядно-обзорное), повышает результативность учебного процесса. Использование НИТ позволяет реализовать такие развивающие цели обучения, как развитие мышления (пространственного, алгоритмического, интуитивного, творческого, теоретического видов мышления), формирование умений принимать оптимальное решение из возможных вариантов, развитие умений осуществлять экспериментально - исследовательскую деятельность (например, за счет реализации возможностей компьютерного моделирования), формирование информационной культуры, умений осуществлять обработку информации.
В данной работе предлагается методика организации самостоятельной работы студентов с помощью разработанного программного комплекса.
Программный комплекс можно условно разделить на следующие основные разделы:
- Историческая справка; основные направления использования изучаемого раздела, практическая значимость; основные теоретические результаты.
- Решение опорных задач по всем разделам, включенным в программу вуза.
- Индивидуальные задания с элементами тренинга.
- Справочный материал.
Рассмотрим более подробно наполнение вышеприведенных разделов, на примере изучения одного из разделов высшей математики, входящего в абсолютное большинство стандартов специальностей технических вузов: «Гармонический анализ (Ряды Фурье)», (например, в государственные стандарты специальностей 210200, 101200, 290300 и т.д.).
В первом разделе приводится короткая историческая справка о возникновении и развитии гармонического анализа. Здесь же излагаются связанные с историей развития гармонического анализа вопросы об основных направлениях использования рядов Фурье для апроксимации периодических функций, сопоставление рядов Тейлора и рядов Фурье. Далее, в этом разделе следуют теоретические положения: общий вид ряда Фурье, теоремы о разложимости периодической функции в ряд Фурье, о сходимости ряда Фурье, определение коэффициентов ряда Фурье и т.д. При этом используются результаты, содержащиеся в четвертом справочном разделе. На основании результатов приложения, приводятся различные виды формул для определения коэффициентов ряда Фурье ![]() ,
, ![]() -периодических функций и для функций, заданных на произвольном отрезке, с произвольным периодом, как по синусу, так и по косинусу кратных углов.
-периодических функций и для функций, заданных на произвольном отрезке, с произвольным периодом, как по синусу, так и по косинусу кратных углов.
Во втором разделе представлены решения большого круга задач о разложении конкретных функций в ряд Фурье
Решение всех задач второго раздела, построение графиков основано на использовании системы «Mathematica». При этом студентам демонстрируется различные приближения ряда Фурье.
Так, например, на рисунке представлено приближение ![]() -частичными суммами ряда Фурье для функции
-частичными суммами ряда Фурье для функции
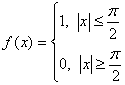 ,
,
при ![]() 5, 10, 25, 50 соответственно.
5, 10, 25, 50 соответственно.
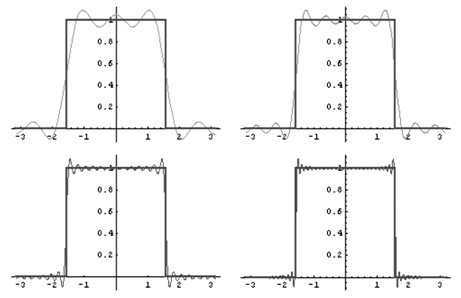
График 1.
В следующем разделе студент из набора задач выбирает по определенному паролю индивидуальные задания. В процессе их выполнения студент вводит результаты промежуточных вычислений; в случае неправильного ответа программа отсылает исполнителя к соответствующему разделу теоретического или практического материала, в том случае если ошибка повторяется несколько раз на мониторе появляется правильный ответ и программа предлагает продолжить решение дальше, и только после получения правильного решения студент может перейти к выполнению следующего этапа самостоятельной работы. По окончании работы программа предоставляет возможность распечатать полученные результаты для проверки и оценки преподавателем.
Изложенная выше методика организации самостоятельной работы студентов может быть использована для любых форм самостоятельной работы: дистанционное обучение, заочная форма обучения, самостоятельного изучения разделов программы и прочее.
Внедрение этих пакетов в учебный процесс позволяет повысить заинтересованность студентов в изучении математических дисциплин, и как следствие, качество подготовки по математике и связанными с ней техническими дисциплинами.
Список литературы
- Ершова А..П. Концепция использования средств вычислительной техники в сфере образования: Информатизация образования.-Новосибирск, 1990.-58с.
- Капустина Т.В. Компьютерная система Mathematica 3.0 в вузовском образовании.-М.: Изд-во МПУ, 2000. - 240с.:ил.
- Пловина И.П. Педагогические программные средства. 4.1. Основные идеи: Методические рекомендации для разработчиков ППС.-Омск: Республиканский Центр ПИТО, 1991. - 70с.
- Шапкин В.В. Педагогические средства как базовый элемент информационной технологии обучения. // Проблемы применения ЭВМ в профессионально-технических учебных заведениях стран-членов СЭВ. Сб. научных трудов.-Ленинград, 1989.-С. 20-30.



