Моделированию струйных течений вязких сред посвящено большое количество работ. В основном они базируются на моделях невязкой сжимаемой жидкости (газа) или моделей несжимаемой вязкой жидкости при условии турбулентности потока. В отличие от предыдущих, в данной работе при моделировании струйных течений вязких несжимаемых сред использовалась система уравнений механики сплошной среды: уравнения движения и неразрывности, при ламинарном режиме течения потока жидкости. При этом использовались следующие допущения:
- Нестационарность гидродинамических процессов обусловлена зависимостью от времени расхода жидкости G, поступающей в некоторую область трёхмерного пространства, которая может быть как ограниченной так и неограниченной;
- Рассматриваемые жидкости являются не сжимаемыми средами, т.е. удовлетворяют гипотезе постоянства плотности ρ.
- Реологическое поведение жидкостей характеризуется гипотезой ньютоновской жидкости, т.е. динамическая вязкость жидкостей μ является постоянной величиной.
- Объёмные силы, влияющие на процессы течения, являются силами тяжести;
Для учета осесимметричности струйных течений использована цилиндрическая система координат (r, φ, z). При этом все переменные задачи становятся независимыми от угла φ. Система уравнений движения и неразрывности этом случае записывается в виде:
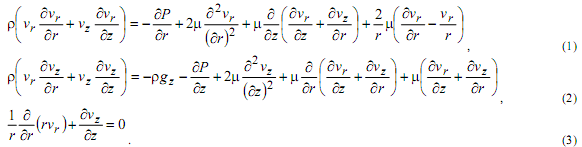
Для закрученных струй система уравнений движения и неразрывности примет вид:
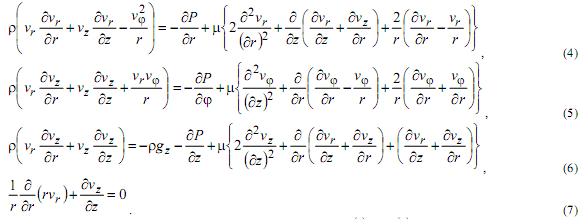
Для получения конкретных решений эта область заменяется прямоугольной с заранее неизвестными значениями высоты hz и радиуса hr , которые уточняются в ходе решения задачи итерационным методом. Постановка граничных условий в этом случае отличается от постановки граничных условий для стеснённых струй, тем, что на границе ставится условие распределения давления при отсутствии струй.
В качестве граничных условий примем:
1. На круговом секторе - части ABC, считаем заданным профиль скорости
![]() (8)
(8)
где fr(r), fz(z) - функции, зависящие от характера поступления жидкости в подающие отверстия, δ - диаметр отверстия. На функции fr(r), fz(z) накладываются следующие соотношения, имеющие простой физический смысл:
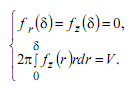 (9)
(9)
Так в простейшем случае функции fr(r), fz(z) имеют вид:
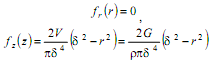 (10)
(10)
где V - объемный расход через одно подающее отверстие, м3/с; G - массовый расход через одно отверстие, кг/с.
В качестве другого примера функций fr ( r), fz (z) - можно использовать зависимости, полученные из предположения, что жидкость поступала в отверстия через плавно сужающиеся или плавно расширяющиеся конические каналы, конкретные виды этих зависимостей могут быть получены из решения соответствующей задачи течения в конических каналах.
2. На остальной части сектора ABC используется условие прилипания жидкости:
![]()
3. На АВВ2А2 , АСС2А2 выполняется условие симметрии течения:
![]()
![]() - нормаль к границам АВВ2А2 , АСС2А2.
- нормаль к границам АВВ2А2 , АСС2А2.
4. На А2В2С2 примем, что
p=const, при ![]() (13)
(13)
и так как давление определяется с точностью до постоянной величины, можно положить
p = 0 при 0 ≤ r ≤ hr , z = hz (14)
Для получения наиболее общего решения запишем задачу в безразмерном виде. Для этого введём безразмерные координаты
![]() (15)
(15)
безразмерные скорости
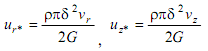 (16)
(16)
и безразмерное давление
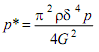 (17)
(17)
Тогда система уравнений движения и неразрывности запишется в виде
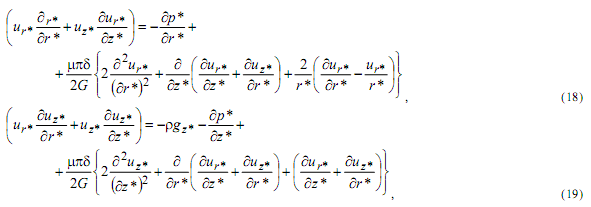
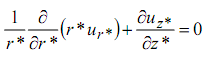
Граничные условия примут вид:
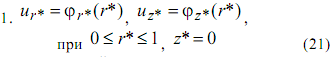
где для простейшего случая
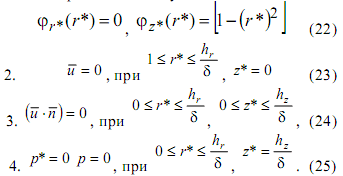
Таким образом, решение задачи течения объемной осесимметричной свободной затопленной струи вязкой жидкости зависит от параметров 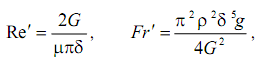
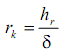 и от профилей скорости на выходе из отверстий
и от профилей скорости на выходе из отверстий ![]()
Работа выполнена при финансовой поддержке РФФИ (грант №05-08-65508) и гранта Президента РФ №МК-9718.2006.8.
Работа представлена на VII научную конференцию с международным участием «Успехи современного естествознания», Дагомыс (Сочи), 4-7 сентября 2006. Поступила в редакцию 28.08.2006г



