Несмотря на определенные успехи, достигнутые в изучении распространения оптических импульсов в диспергирующей среде, к которой относятся волоконные световоды, интерес к этому вопросу не ослабевает. Решая даже задачи линейной оптики, не всегда удается получить их точное описание. В настоящее время удалось осуществить генерацию световых импульсов длительностью в несколько колебаний поля и мощностью более 109 Вт/см2. Структура таких импульсов существенно отличается от общепринятых моделей модулированных квазимонохроматических сигналов с прямоугольной или гауссовой огибающей. Традиционные решения уравнений Максвелла в прозрачных средах связаны с представлением в виде произведений функций, зависящих либо от координаты, либо от времени (разделяющиеся решения). При этом временная зависимость обычно исследуется с помощью преобразования Фурье. Многие десятилетия такой подход формировал язык описания квазимонохроматических волн в оптике, однако, попытки применить этот же подход в динамике взаимодействия коротких видеоимпульсов с диспергирующими средами натолкнулись на неожиданные трудности, как концептуальные, так и вычислительные. При Фурье-преобразовании огибающая сигнала конечной длительности усредняется по бесконечному интервалу времени. Участки быстрого изменения огибающей, которые являются наиболее важными для регистрации сигнала в телекоммуникационных системах, оказываются при этом скрытыми. С другой стороны, для восстановления временной огибающей локализованного сигнала с помощью обратного Фурье-преобразования необходимо исключить поля гармоник вне области локализации. Однако, для уточнения области локализации требуется учитывать все возрастающее количество гармоник. Деформация импульса в диспергирующей среде описывается, как известно, в частотной области методом разложения фазы в ряд по степеням отношения спектральной ширины импульса 
к несущей частоте ω. К сожалению, для коротких широкополосных импульсов, содержащих одно или несколько колебаний поля, отношение 
, не является малым параметром. При этом количество спектральных компонент, требуемое для синтеза поля импульса в глубине среды, становится непомерно большим. Следует отметить, что трудности связаны не с уравнениями Максвелла, а с традиционным методом их решения с помощью разделения переменных и преобразований Фурье. Этот способ удобен для описания квазимонохроматических волн с медленно меняющейся амплитудой и фазой, но малоэффективен для анализа нестационарных и негармонических полей.
Предлагается новый подход к решению уравнений Максвелла, который позволяет получить точные аналитические решения не связанные со стандартным разделением переменных и вне рамок разложений Фурье. Такие решения образуют математическую основу описания быстропеременных непериодических полей и коротких импульсов в различных средах. Модель дисперсионной эволюции сверхкороткого оптического импульса, распространяющегося в линейной диспергирующей среде, может быть представлена в виде решений уравнения Клейна-Гордона, которое в безразмерной форме выглядит следующим образом:
.
Тогда решениями данного уравнения является выражение:
,
где 
.
Функция 
имеет вид
,
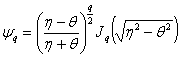где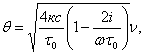 
,
,
,
,
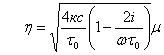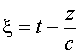k - коэффициент поглощения среды;
ω - частота оптической несущей;
- характерный промежуток времени, пропорциональный времени релаксации (длительность падающего импульса);
Осуществляя переход к переменным 
, получим
.
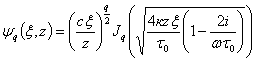Коэффициенты 
можно определить из начальных и граничных условий. Исходя из прямоугольного фронта падающего импульса для первой гармоники, имеем
,
следует 
= 2,
где E0 - начальная амплитуда электрической составляющей поля.
Следует отметить, что первая гармоника является определяющей при формировании фронта огибающей электрической составляющей поля. Остальными составляющими можно пренебречь. Тогда огибающая электрического поля для первой гармоники принимает вид:
.
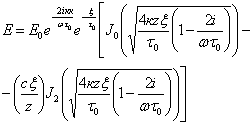Таким образом, получено точное решение волнового уравнения в линейной оптической среде, не связанное с традиционными допущениями о медленности изменения параметров среды или поля.