Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Золотым сечением или делением в крайнем и среднем отношении положительной величины  называется ее разделение на две такие части  и , чтобы  было средним геометрическим между  и [1]. Из равенства  путем решения квадратного уравнения

                                 (1)

отбрасывая отрицательный корень, находим:

                                 (2)   

Записывая (1) в виде:

замечаем, что a есть среднее геометрическое чисел x и x+a.

Таким образом, если делит число в золотом сечении, то  в свою очередь делит в золотом сечении число .

Обозначим

                       (3)

           (4)

Очевидно, ,

где x определяется согласно (2).

Золотое сечение (aurea section) известно с древних времен и используется в архитектуре, живописи и т.д. [2]. В теории музыки отношение длин струн, равное φ, создает гармонический аккорд. На золотом сечении основаны природные гармонии.

На наш взгляд, представляют интерес задачи механики, где также обнаруживается золотое сечение. В статье решено несколько таких задач, относящихся к теме определения центров тяжести (центров масс) тел.

Задача 1.

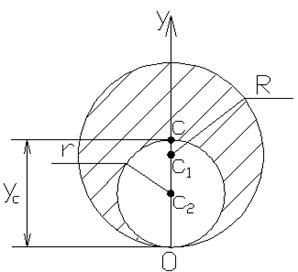
Рисунок 1. Однородный круг радиусом R

Каков должен быть радиус r, чтобы центр тяжести оставшейся фигуры находился в точке c?

Решение. Заштрихованная фигура симметрична относительно оси OY. Поэтому ее центр тяжести находится на этой оси, и его положение полностью определяется координатой y_c. Применим метод отрицательных масс [3]. Дополним нашу фигуру до круга радиуса R и примем, что этот круг с площадью S₁ и центром масс (центром тяжести) c₁ полностью заполнен массой (имеет положительную площадь). На круге радиуса r распределим отрицательную массу (отрицательную площадь) той же плотности. Площадь этого круга с отрицательной массой обозначим - S₂ (S₂ >0 ), а ее центр масс - c₂.

Согласно методу имеем

                                   (5) 

или

Сокращая на , получим относительно r квадратное уравнение

                                       (6)

которое с точностью до обозначений совпадает с уравнением (1). Положительный корень уравнения (6) равен:

Координата центра тяжести:

                     (7)

Отсюда видно, что y_c делит вертикальный диаметр большого круга в золотом сечении. Отметим следующее свойство золотого сечения в этой задаче: если диаметр вырезаемого круга меньше золотого сечения, то центр тяжести оставшейся фигуры находится внутри нее, если больше золотого сечения, то - вне ее. Следует сказать, что аналогичное свойство сохраняется и в задачах 2 и 3.

Задача 2.

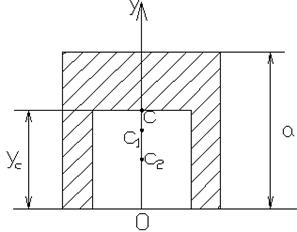
Рисунок 2. Однородная квадратная пластина с симметричным вырезом

Из однородной квадратной пластины со стороной  вырезают квадрат так, что стороны обоих квадратов параллельны. Фигуры имеют вертикальную ось симметрии - Oy (рис. 2). Какова должна быть сторона меньшего квадрата для того, чтобы центр тяжести оставшейся после выреза части совпал с точкой с

Решение. Очевидно, что точка с лежит на оси симметрии, поэтому x_c =0. Для нахождения y_c вновь воспользуемся методом отрицательных масс. Опираясь на (5) получим

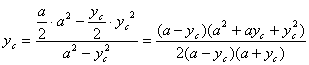
После сокращения на  имеем относительно y_c квадратное уравнение

                               (8)

совпадающее с уравнением (1). Положительный корень уравнения (8) равен . Видим, что y_c делит сторону  в золотом сечении.

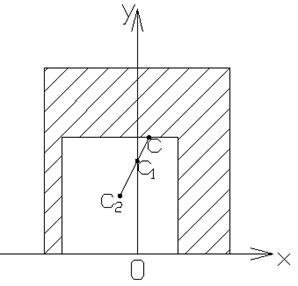
Рисунок 3. Однородная квадратная пластина с асимметричным вырезом

Рассмотрим случай, когда вырезаемый квадрат расположен асимметрично относительно оси OY, например, смещен влево (рис.3).

Тогда центр тяжести оставшейся фигуры смещается вправо по горизонтали. Абсцисса центра тяжести определяется по формуле

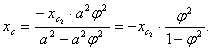
Отсюда

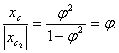
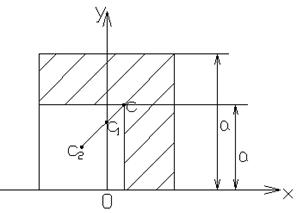
Рисунок 4. Однородная квадратная пластина с угловым вырезом

Отметим также, что точки  принадлежат одной прямой. При этом точка c₁ делит отрезок c₂c в золотом сечении, т.е.

                      (9)

            (10)

На рисунке 4 показан случай, когда меньший квадрат со стороной  занимает крайнее положение. Центр тяжести c находится на вершине малого квадрата и делит в золотом сечении как стороны, так и диагональ большого квадрата.

Задача 3.

Из однородного прямоугольника со сторонами  и  ( ) вырезан прямоугольник со сторонами a₁ и  так, что стороны обоих прямоугольников параллельны. Прямоугольники симметричны относительно оси OY. Какова должна быть величина  для того, чтобы центр тяжести оставшейся части совпал с точкой c (рис. 5)?

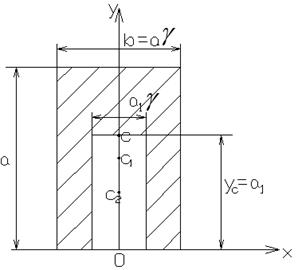
Рисунок 5. Однородная прямоугольная пластина с симметричным вырезом

Решение. Применяем метод отрицательных масс. Точки  обозначают соответственно центр тяжести большого и малого прямоугольников. В силу симметрии . Для нахождения y_c имеем уравнение:

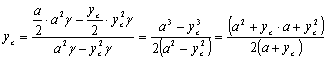
После преобразования получим квадратное уравнение, совпадающее с уравнением (8). Положительный корень уравнения равен .

Если прямоугольник вырезать так, как показано на рис. 6, то точки  расположатся на диагонали прямоугольников. В случае соответствующем рис. 6, центр тяжести делит в золотом сечении обе стороны большого прямоугольника и его диагональ.

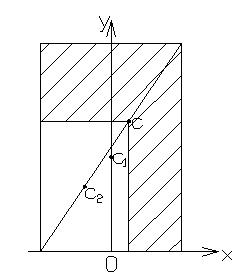
Рисунок 6. Однородная прямоугольная пластина с угловым вырезом

Заметим, что хотя задача 2 является частным случаем задачи 3, целесообразно было рассмотреть ее отдельно.

В учебниках и задачниках по теоретической механике и сопротивлению материалов достаточно много задач об определении положения центра тяжести плоских фигур, имеющих вырезы, отверстия. Автору известна только одна задача, когда ответ совпадает с золотым сечением [4]. Речь идет о варианте задачи 2, соответствующем рис. 4.

Пусть невесомый горизонтальный стержень  в точке  закреплен шарнирно. Каково должно быть отношение между силами , перпендикулярными стержню и приложенными в точках c₁ и c₂, чтобы стержень находился в равновесии (рис. 7)?

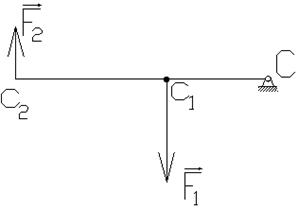
Рисунок 7. Невесомый горизонтальный стержень

При равновесии сумма моментов сил  и относительно точки C равна нулю, т.е.

Отсюда получаем

Учитывая, что , имеем

                                       (11)

где S₁ - площадь исходной фигуры (круга, квадрата, прямоугольника), S₂ - площадь соответствующей вырезанной фигуры.

Задача 4.

Дано тело, состоящее из двух однородных стержней (рис. 8).

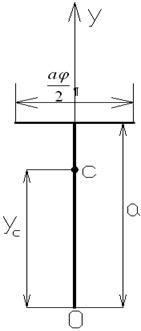
Рисунок 8. Тело из двух однородных стержней

Длина вертикального стержня равна , горизонтального - . Ось OY является осью симметрии. Плотности обоих стержней одинаковы. Требуется найти центр тяжести этого сложного тела.

Решение. Используя метод разбиения [3], получаем

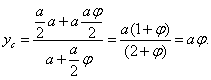
Видно, что центр тяжести делит вертикальный стержень в золотом сечении. Очевидно, решение сохранится, если горизонтальный стержень заменить эквивалентным точечным грузом, закрепленным на верхнем конце вертикального стержня.

Задача 5.

Тело состоит из трех однородных стержней (рис. 9).

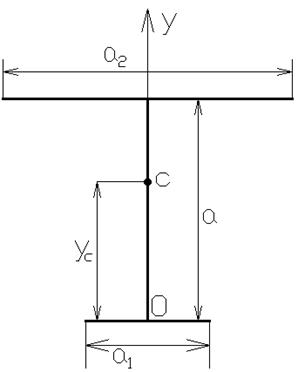
Рисунок 9.

Длина вертикального стержня равна , длины прикрепленных к его концам горизонтальных стержней равны , где Ф дается согласно (4). Плотности всех стержней одинаковы. Вертикальный стержень совпадает с осью симметрии. Требуется найти центр тяжести сложного тела.

Решение. Центр тяжести расположен на оси симметрии. Разбивая сложное тело на 3 части, находим

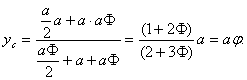
Видим, что центр тяжести делит вертикальный стержень в золотом сечении.

Задача 6.

Дана однородная пластина в форме равнобедренной трапеции с основаниями  и  и высотой h, расположенная симметрично относительно оси OY (рис. 10).

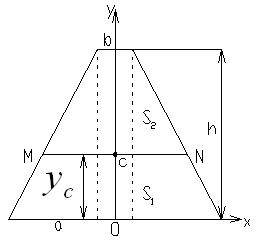
Рисунок 10.

Так как ордината центра тяжести c заключена в интервале , то существует трапеция, для которой

,                       (12)

т.е. имеет место золотое сечение.

Требуется определить условие, когда центр тяжести трапеции совпадает с золотым сечением.

Решение. Ордината центра тяжести произвольной равнобедренной трапеции находится по следующей формуле:

                           (13)

Выражая меньшее основание трапеции через большее, т.е. полагая  (0<γ<1) и подставляя в формулу (13) с учетом (12) получим

                                   (14)

Таким образом, чтобы центр тяжести равнобедренной трапеции делил ее высоту в золотом сечении, необходимо выполнение условия (14).

Обозначим через p длину отрезка MN, проходящего через центр тяжести параллельно основаниям. Представим площадь S исходной трапеции как сумму (см. рис 10), т.е. .

Отсюда находим

или

.                      (15)

Равенство (15) можно получить также из простых геометрических соображений.

Заключение

Получены решения ряда задач определения центра тяжести однородных фигур и стержневых тел, сводящиеся к золотому сечению. Показаны некоторые свойства задач. Как частный случай получен ранее известный результат.

Автор выражает благодарность студенту группы НР-04 СИНГ ТюмГНГУ Ильющенко В.И. за помощь в оформлении работы.

СПИСОК ЛИТЕРАТУРЫ

1. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов. - 13-е изд., исправленное. - М.: Наука, гл. ред. физ-мат. лит., 1986. - 544с.
2. Волошинов А.В. Математика и искусство. - М.: Просвещение, 1992. - 335с.
3. Никитин Н.Н. Курс теоретической механики: Учебник для машиностроительных и приборостроительных специальностей вузов. -5-е изд. переработанное и дополненное. - М.: Высшая школа, 1990. - 607с.
4. Сборник задач по теоретической механике: Учеб. пособие для студентов технических вузов /Бражниченко Н.А. и др. - 4-е изд., исправленное и дополненное. - М.: Высшая школа, 1986. - 480с.