Частица материала, опирающаяся на винтовую поверхность пружинной спирали и прижатая к стенке кожуха, для общего случая наклонного расположения оси спирально-винтового пружинного транспортера имеет движение, описываемое дифференциальными уравнениями:
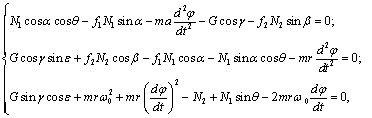
Решения данной системы показывают, что период неустановившегося движения в спирально-винтовых пружинных транспортерах является кратковременным, и уже по истечении нескольких секунд движение становится устойчивым, с постоянными значениями средней осевой скорости υ и абсолютной угловой скорости w вращательного движения.
Из данной системы при 
m = 1, G = mg = 1g = g находятся реакции:
Из третьего уравнения системы при подстановке N1 и N2, следует
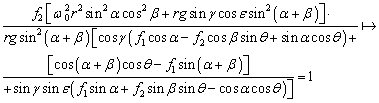
Практическую ценность составляет вопрос о выявлении режима, при котором β = 90° и частица будет иметь скорость 
, параллельную оси транспортера, т.е. когда
.
А так же конструкторский интерес представляет задача о выявлении угла наклона винтовой линии пружины, при котором обеспечиваются максимальная скорость и производительность его. Дифференцируя 
, находим:
. Из условия 
получаем: 
.
Этот результат совпадает с тем, который получается в спирально-винтовом пружинном транспортере при максимальном коэффициенте полезного действия.