Введение. В работе исследуется возможность построения функциональной зависимости между фрактальной размерностью D действительной части фрактальной функции Вейерштрасса - Мандельброта (ФВМ) при тождественно нулевой случайной фазе и моментом от УРД при оценке с помощью ФВМ микроускорений [1]. Сама ФВМ в этом случае имеет вид [2]:
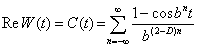 (1)
(1)
Ранее [3, 4, 5] было выяснено, что параметр t связан с безразмерным временем протекания технологического процесса на борту космического аппарата (КА) и изменяется от 0 до 1. Также был проведен ряд исследований, который показал качественную связь между фрактальной размерностью D и моментом от управляющих ракетных двигателей системы ориентации и управления движения КА (УРД). Подробно постановка задачи и суть, а также развитие и современное состояние проблемы микроускорений рассмотрены в работах [6, 7, 8]. В работах [5, 9] показано, что в коридоре значений фрактальной размерности:
![]() (2)
(2)
ФВМ соответствует понятию случайная величина. Поэтому исследования проводились именно в коридоре (2). Как известно [10], самая опасная квазистатическая компонента микроускорений практически не демпфируется во времени и тоже может быть представлена как случайная величина.
Постановка задачи. Для формирования функциональной зависимости между фрактальной размерностью ФВМ D и моментом от УРД требуется проведение исследований по влиянию фрактальной размерности ФВМ (1) в коридоре (2) на основные числовые характеристики ФВМ как случайной величины. Наиболее важной частью является исследование динамики изменения среднего значения, т.к. фактически это и есть средний уровень микроускорений по фрактальной модели, с одной стороны, и именно благодаря увеличению момента от УРД повышается средний уровень микроускорений в реальных условиях, а поскольку D как раз моделирует этот момент, то полученные результаты будут играть решающую роль в оценке микроускорений с помощью ФВМ, с другой стороны.
Таким образом, ставиться задача исследования изменения среднего значения функции (1) в коридоре (2) при изменении параметра b от 0 до 1.
Основные результаты работы. На рис. 1 показаны зависимости среднего значения выборки из 1000 точек ФВМ (1) на отрезке ![]() с равномерным шагом
с равномерным шагом ![]() при различных значениях ее параметров D и b.
при различных значениях ее параметров D и b.
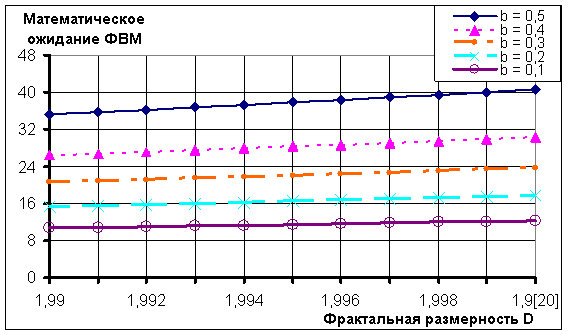
Рисунок 1. Динамика изменения среднего значения ФВМ в коридоре (2)
На рис. 1 1,9[20] обозначает двадцать девяток после запятой. Дело в том, что фрактальная (дробная) размерность должна быть строго меньше двух. Сама же ФВМ после этого значения D перестает изменяться при дальнейшем увеличении фрактальной размерности настолько, что ни одно из тысячи выбранных значений ФВМ при D = 1,9[20] не отличается от аналогичных значений ФВМ при D = 1,9[25] или D = 1,9[30]. Такой же эффект наблюдается и при приближении D к левой границе (D>1 ).
Как видно из рис. 1, зависимости среднего значения от фрактальной размерности D для всех рассмотренных b практически линейны с едва уловимой долей нелинейности. Выбор диапазона значений b связан, прежде всего, с тем что, как показано в работе [11], при 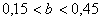 ФВМ подчиняется закону нормального распределения. Вообще говоря, при построении фрактальной модели микроускорений диапазон значений b предлагается искусственно ограничить: 0 < b < 1, т.к. при переходе через 0 и 1 ФВМ существенно изменяется - это легко понять из формулы (1). Нелинейность хорошо заметна при наблюдении динамики изменения верхней и нижней границы среднего значения в зависимости от b (рис. 2).
ФВМ подчиняется закону нормального распределения. Вообще говоря, при построении фрактальной модели микроускорений диапазон значений b предлагается искусственно ограничить: 0 < b < 1, т.к. при переходе через 0 и 1 ФВМ существенно изменяется - это легко понять из формулы (1). Нелинейность хорошо заметна при наблюдении динамики изменения верхней и нижней границы среднего значения в зависимости от b (рис. 2).
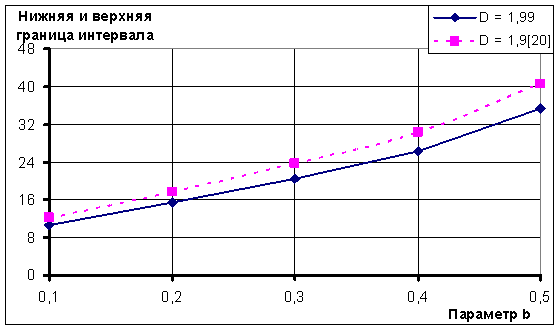
Рисунок 2. Динамика изменения верхней и нижней границ среднего значения ФВМ в коридоре (2)
Как видно из рис.2, кривые изменения значений верхней и нижней границ расходятся. Это говорит о том, что b также оказывает влияние на среднее значение, хотя и очень незначительное. Правильнее говорить о том, что диапазон значений D слишком мал, чтобы на нем наблюдалось значительное влияние b.
Если зависимости, представленные на рис. 1, моделировать с помощью линейной модели парной регрессии, то влияние b на среднюю линейную производную (коэффициент перед регрессором) является весьма ощутимым (рис. 3).
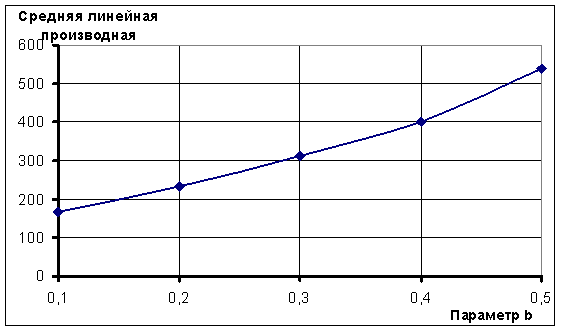
Рисунок 3. Динамика изменения средней линейной производной
Хотя относительный рост линейной производной, отнесенный к величине этой производной, не превышает 1,5% (рис. 4).
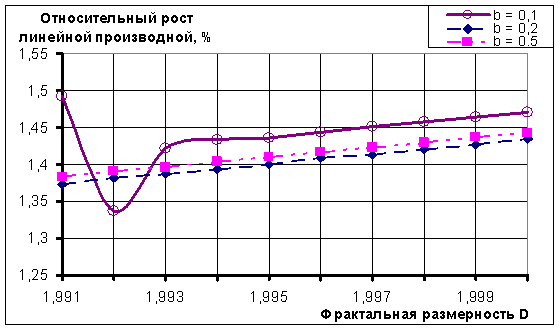
Рисунок 4. Динамика изменения относительного роста средней линейной производной
Рис. 4 наглядно показывает, что этим изменением можно пренебречь и считать коэффициент перед регрессором является постоянным. Вместе с этим можно и пренебречь влиянием b на среднее значение без ущерба для точности.
Основные выводы по работе. Проведенные исследования показывают, что среднее значение ФВМ (1) в коридоре изменения фрактальной размерности D (2) практически линейно возрастает с ростом самой D. Параметр b оказывает слабое влияние на динамику этого роста: при бОльших значениях b прирост ФВМ оказывается более существенным.
При оценке микроускорений с помощью ФВМ без проведения дополнительных исследований можно утверждать о линейной зависимости среднего значения ФВМ от D в рассматриваемом диапазоне (2), где ФВМ соответствует понятию случайная величина.
Для формирования функциональной зависимости D от момента УРД необходимо провести такие же исследования о влиянии изменения момента на создаваемый средний уровень микроускорений внутри КА в постановке задачи, когда демпфирование собственных колебаний упругих элементов КА либо отсутствует вовсе, либо пренебрежимо мало, а сами микроускорения (точнее их квазистатическую) компоненту можно также, как и ФВМ считать случайной величиной.
На первый взгляд кажется, что ограничения, наложенные на D, являются искусственными, однако, в реальной постановке задачи момент УРД также является ограниченной величиной: он не может быть сколь угодно мал или, наоборот, велик. Таким образом, можно утверждать, что ограничения (2) являются естественными ограничениями, наложенными на мощность, а, следовательно, и момент УРД КА.
СПИСОК ЛИТЕРАТУРЫ
- Седельников А.В., Бязина А.В., Антипов Н.Ю. Использование функции Вейерштрасса-Мандельброта для моделирования микроускорений на борту КА //Сборник научных трудов X Всероссийского научно-технического семинара по управлению движением и навигации ЛА. Самара. 2002. с. 124-128.
- Седельников А.В., Бязина А.В. Использование фракталов в математическом моделировании// Сборник научных трудов в Самарском филиале УРАО. вып. 2-3. Самара. 2002. с. 72 - 85.
- Седельников А.В., Бязина А.В., Иванова С.А. Статистические исследования микроускорений при наличии слабого демпфирования колебаний упругих элементов КА //Научные чтения в Самарском филиале РАО. - Часть 1. Естествознание. - М.: Изд. УРАО. - 2003. - 137 - 158.
- Седельников А.В. Исследование функции распределения уровня микроускорений во времени// Успехи современного естествознания. - № 9. - 2004. - с. 15 - 18.
- Седельников А.В., Корунтяева С.С., Чернышева С.В. Анализ влияния параметров функции Вейерштрасса-Мандельброта на ее закон распределения //Современные наукоемкие технологии. - 2005 г. - № 9. - с. 43-46.
- Седельников А.В. Проблема микроускорений: 30 лет поиска решения //Современные наукоемкие технологии. - 2005 г. - № 4. - с. 15-22.
- Седельников А.В. Статистические исследования микроускорений как случайной величины// Фундаментальные исследования. №6. 2004. с. 123-124.
- Седельников А.В., Бязина А.В. Исследование законов распределения микроускорений, смоделированных с помощью функции Вейерштрасса-Мандельброта и полученных в результате эксперимента //Современные проблемы механики и прикладной математики. - Сборник трудов международной школы-семинара. - Ч. 1. - т. 2. - Воронеж. - 2004. - с. 450-453.
- Седельников А.В., Корунтяева С.С., Чернышева С.В. Проверка закона нормального распределения фрактальной функции Вейерштрасса-Мандельброта //Успехи современного естествознания. - 2005 г. - № 11. - с. 37-38.
- Авраменко А.А., Седельников А.В. Моделирование поля остаточной микрогравитации на борту орбитального КА //Изв. Вузов Авиационная техника. - 1996. - №4. - с. 22-25.
- Седельников А.В., Чернышева С.В. Моделирование микроускорений фрактальной функцией Вейерштрасса-Мандельброта для случая малого демпфирования //Материалы XXX-х Академических чтений по космонавтике. - Москва. - 2006. - с. 100-101.



