Сила реакции излучения это та сила, которая действует на заряженную частицу со стороны создаваемого ей поля электромагнитного излучения. В классической электродинамике с этой силой связано внутреннее противоречие, что указывает на неполноценность данной теории. В работе [1] приведена формула этой силы fs, выведенная в рамках модернизированной электродинамики, но только для частного случая ускоренного движения заряда. В этом сообщении демонстрируется общий случай. В основу метода вывода положена типовая феноменологическая методика определения силы реакции излучения через мощность излучения Р0.
При вычислении мощности излучения нас будет интересовать поле на больших расстояниях от заряда и в пределе при R=│r-r0(t)│→∞, тогда положим R ≈ r(1-err0/r) →r, eR → er= r/r. Мощность через элемент сферической поверхности dS равна
![]()
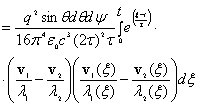 ,
,
где П0=[EизHиз]- вектор Пойтинга, при этом уравнения для Eиз, Hиз приведены в [2]; θ-угол между векторами er и v; ψ-азимутальный угол; λ1=1- (erv1)/c; l2=1- (erv2)/c; v1=v(t´1); v2=v(t´2); eR1 =R1/R1; eR2=R2/R2; R1=R(t´1); R2=R(t´2).
Рассмотрим ускорение по прямой со скоростями (v/c<<1), при этом имеем: (erev) =cosθ; v1= v1ev; v2= v2ev, где ev= v/v. Полная излучаемая мощность
![]() (1)
(1)
Формула (1) не зависит от R, поэтому она правомерна в любой точке, в том числе и на границе области генерации поля излучения (R=Rm), [2].
Из уравнения движения заряда dR/dt = d│r-r0(t)│/dt = - (Rv)/R = - (eRv) устанавливаем связь между расстоянием R(t) от заряда до наблюдателя и параметрами движения в разные опорные моменты времени:
![]() ,
,
![]() (2)
(2)
В работе [2] изучен характер излучения поля на разных этапах времени от начала ускорения. Задавая R(t)=Rm=πtс и tгр =R(0)/c+πt из [2], получаем выражение:
![]() ,
,
из которого (при условии v/c<<1) следуют соотношения R(t´1)≅Rm, R(0)≅Rm в запаздывающие моменты времени. Подставляя их в формулы для tгр и t¢1 из [2], имеем:
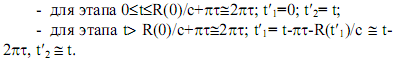
Подставляя теперь полученные моменты времени в (1), получаем законы излучения.
Определяем силу реакции излучения fs. В классической электродинамике сила реакции излучения выводится из баланса между работой, произведенной этой силой над зарядом и энергией излучения на интервале времени Т, за который заряд возвратился бы в исходное состояние движения. Так как выражение (1) содержит затухающую экспоненту по времени, тогда возврат в исходное состояние возможен на бесконечном пределе времени, начиная с момента времени tА→∞ до tВ = tА+Т
![]() . (3)
. (3)
Для 0≤t≤2πt: t´1=0 и если v1=v(0)≠0, то соответствующим выбором инерциальной системы отсчета всегда начальную скорость можно свести к нулю, v1 = 0. При этом v2=v, поэтому непосредственно находим fs = Р0/v, которая имеет вид:
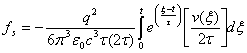 (4)
(4)
Сила (4) отрицательная, значит, ей соответствует устойчивое уравнение движения.
Для t≥2πt, переходя к новой шкале времени на основе преобразования t´= (t-2πt), имеем
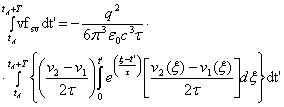 . (5)
. (5)
Применяя к правой части (5) процедуру интегрирования по частям, имеем:
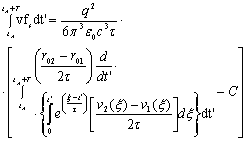 (6)
(6)
где при tА→∞,
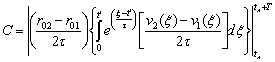 → 0,
→ 0,
Используем следующее упрощение: (r02-r01)≅ 2πtv, (v2-v1) ≅ 2πta, где v, a - усредненные на интервале 2πt скорость и ускорение соответственно. Из (5)-(6) следует выражение для силы реакции излучения
![]() ,
, ![]() . (7)
. (7)
Этой силе соответствует в операторной форме следующее уравнение движения заряда:
L[a][p(t-tо)+1]=(1+pt)L[f/m]. (8)
При t³tо движение устойчивое (tо≅10-24с), где L[a], L[f]-операторные ускорение и сила соответственно, p - оператор Лапласа, m-масса электрона. В данной теории параметр Rm=πс определяет область генерации излучения. В квантовой теории электрон характеризуется областью виртуальных фотонов с размером, равным комптоновской длине волны λKЭ. Если оценить Rm≈λKЭ?, тогда имеет место приближение t ≈ 10-21с >tо.
СПИСОК ЛИТЕРАТУРЫ
- Меньшов Е.Н. Новые уравнения Максвелла: преодоление внутреннего противоречия в классической электродинамике//Современные наукоемкие технологии. - 2005. - №1. - С.89-90.
- Меньшов Е.Н. Поле излучения, определяемое из новых уравнений Максвелла //Современные наукоемкие технологии. - 2005. - №11- С.61-63.



