Вопросам взаимодействия электромагнитных полей со средами с временными изменениями электромагнитных параметров (диэлектрической и магнитной проницаемостей, проводимости) посвящено много публикаций [1-6]. Рассматривались волны в природных средах (ионосфера, флуктуирующие слои тропосферы и др.), искусственных средах (ядерный взрыв, плазма в газоразрядных лампах и др.); в плазменных образования, при релаксации среды после прохождения лазерного импульса. Метод модового базиса [3,5,6] удобен для исследования колебаний в резонаторах с нестационарной, неоднородной средой; для разработки нового подхода к изучению электромагнитных волн в нестационарных волноводах и безграничных средах.
Рассмотрим метод построения модового базиса для геометрически регулярных волноводов. Волновод предполагается геометрически регулярным вдоль оси OZ, его поперечное сечение S произвольным. С учетом материальных уравнений:
; 
(1)
систему уравнений Максвелла для поля в волноводе можно записать в виде:
(2)
, 
- плотности электрического и магнитного токов, 
, 
- плотность свободного заряда и плотность заряда сторонних источников.
Граничные условия на стенках:
(3)
Вектора напряженностей электрического 
и магнитного 
полей, представим в виде:
; 
(4)
Представляя оператор Гамильтона в виде продольной и поперечной составляющих 
из векторов и создается четырехмерный вектор-столбец:
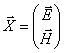(5)
Вводится функциональное пространство четырехмерных вектор-функций 
с энергетической метрикой вида:
(6)
Вводится два матричных дифференциальных оператора:
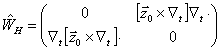(7)
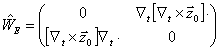(8)
Тогда уравнения (1) - (3) можно представить в виде операторных уравнений:
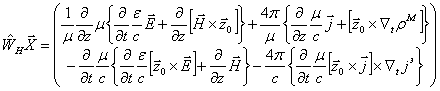(9)
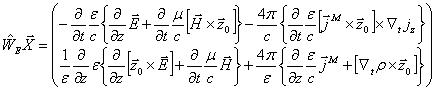(10)
Левые части уравнений (9), (10) включают операторы дифференцирования по поперечным координатам, которые можно дополнить граничными условиями.
Поставим задачу на собственные значения для операторов (7) и (8):
, (11)
(12)
где 
, 
- собственные вектора, а pm и qn - отвечающие им собственные числа. Вектор 
(5) можно разложить в ряд Фурье по системе собственных векторов:
(13)
Подлежат определению коэффициенты Am, Bn.
(14)
(15)
, 
, 
, 
- собственные функции задач Неймана и Дирихле для скалярных мембранных функций:
(16)
(17)
Собственные числа 
и 
в векторных задачах (11), (12) совпадают соответственно с собственными числами в задачах (16), (17).
Для коэффициентов разложения поля по базису 
получается система эволюционных уравнений [5]:
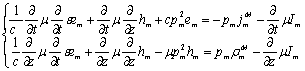
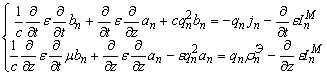
В случае H-волн составляющие векторов напряженностей электрического и магнитного полей 
и 
(4) могут быть представлены в виде:
,
,
,
В случае регулярного волновода с однородной средой, когда диэлектрическая проницаемость изменяется по линейному закону 
напряженность электрического поля Н-волны меняется по закону отличному от гармонического:
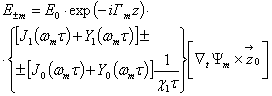
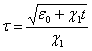. Амплитуда и частота колебаний во времени медленно убывают. Для волновода с нестационарной средой, когда за промежуток времени 10-7 с диэлектрическая проницаемость среды ( X1=107 1/с) меняется от 1 до 2, амплитуда и частота уменьшаются до 0,84 от начальных значений. При X1=105 (1/с) изменение амплитуды составляет менее 1% от начальной, напряженность электрического поля изменяется во времени практически по гармоническому закону. Поперечные и продольные составляющие вектора напряженности магнитного поля в случае H-волн имеют такую же зависимость от времени, как 
.
При изменении диэлектрической проницаемости среды по квадратичному закону:
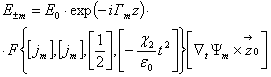
где 
- гипергеометрическая функция с параметрами a1,a2,a3,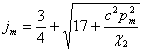 
.
С ростом диэлектрической проницаемости среды, описываемым соотношением амплитуда и частота колебаний вектора напряженности электрического поля медленно уменьшаются. Рост диэлектрической проницаемости приводит к уменьшению амплитуды и частоты колебаний со скоростью, зависящей от параметров модуляции среды x1 и x2.
Установлено, что полученные в данной работе уравнения для коэффициентов разложения векторов напряженностей электромагнитного поля по модовому базису позволяют в отличие от других подходов получить аналитические решения для многих видов функций e(t), что позволяет лучше понять физические свойства структур с нестационарными средами.
СПИСОК ЛИТЕРАТУРЫ
- Шварцбург А. Б., Дисперсия электромагнитных волн в слоистых и нестационарных средах.//Успехи физических наук. 2000. Т. 170. №12. с. 1314-1324.
- Шварцбург А. Б. Отражение электромагнитных волн от нестационарных сред.//Квантовая электроника. 1998. Т. 25. №5. с. 201-205.
- Tretyakov O.A. //Proc. Sino-British Joint Meeting on Optical Fiber Communications. Beijing, 1986. p. 333.
- Назаров З. Ф., Шматько А. А. Электромагнитные колебания в резонансных объемах с нестационарной средой. //Радиотехника и электроника. 1988., Т.33., в.5., с. 1079-1081.
- Третьяков О. А. Эволюционные волновые уравнения.//Радиотехника и электроника. 1989. Т.34., в. 5., с 917-926.
- Глущенко А. Г., Ефимова А. А. Исследование регулярного волновода с модулируемой во времени диэлектрической проницаемостью среды. //Физика волновых процессов и радиотехнические системы. 2004, Т. 7, № 2, с. 36-39.