Психолого-педагогические исследования убедительно показали, что каждому ребенку дарована от природы склонность к познанию и исследованию окружающего мира, то есть детская потребность в исследовательском поиске обусловлена биологически. Очевидно, что правильно поставленное обучение должно совершенствовать эту склонность, способствовать развитию исследовательских умений. С этой целью необходимо вовлекать школьников в учебные исследования, вооружать их методами научно-исследовательской деятельности.
Следуя Е.В. Барановой [1], В.А. Далингеру [3], мы рассматриваем учебные исследования как вид познавательной деятельности, который основан на выполнении учебных заданий, предполагающих самостоятельное выявление учащимися новых для них знаний, способов деятельности и направленных на достижение целей обучения.
Геометрия, в силу своей специфики, предоставляет богатые возможности для организации исследовательской деятельности учащихся. При этом создание гипотезы в геометрических исследованиях основывается на интуиции обучаемых, выполнении ими опытов (экспериментов) и проведении рассуждений.
Использование компьютерных технологий способствует повышению эффективности учебных исследований. Так, установлено, что компьютерная среда позволяет учащимся при индуктивном подходе обнаруживать закономерности в наблюдаемых геометрических явлениях, а при дедуктивном - помогает как формулировать теоремы для последующего доказательства, так и подтверждать уже доказанные факты и развивать их понимание [4]. Важно и то, что компьютер предоставляет возможность провести такой геометрический эксперимент, который в реальных условиях невозможен. Например: около произвольного треугольника описана окружность и, соответсвенно, вписана. Как изменится треугольник, если совместить центры двух окружностей? Традиционными способами такого эксперимента провести нельзя, но с помощью компьютера данная задача вполне разрешима.
В качестве одного из основных программных средств, вовлекающих учащихся в учебные исследования, мы выбрали программу "Живая геометрия". Данная программа позволяет создавать точно вычерченные чертежи и графики, ручное построение которых невозможно, "оживлять" чертежи, плавно изменяя положение исходных объектов, измерять длины, площади и углы с выбранной точностью.
С помощью "Живой геометрии" учащиеся могут создать объект, а затем изучить его математические свойства, просто перемещая объект мышью. Все математические отношения, заложенные при построении, сохраняются, позволяя ученикам изучить целый комплекс аналогичных случаев за несколько секунд. Такой стиль работы подводит школьников к обобщениям самым естественным путем. Таким образом, программа помогает процессу открытия, при котором ученики сначала представляют себе и анализируют проблему, а затем выдвигают гипотезу и пытаются ее доказать.
Например, при изучении темы "Вписанная и описанная окружность" [2] учащимся предлагается включиться в работу, связанную с самостоятельным исследованием свойств описанного и вписанного четырехугольников. Используя инструменты построения и измерения среды "Живая геометрия", школьники должны ответить на вопросы:
- Каковы свойства любого описанного четырехугольника?
- Каковы свойства любого вписанного четырехугольника?
Каждый ученик на экране своего монитора строит окружность, описывает около нее четырехугольник и измеряет его углы и стороны с помощью инстументов "Живой геометрии". Легко изменяя положение вершин четырехугольника, школьник делает собственный вывод, который записывает в текстовом окне на экране. Аналогичная работа проделывается и для вписанного четырехугольника. Выводы коллективно обсуждаются под руководством учителя и формулируются гипотезы:
- В любом описанном четырехугольнике суммы противоположных сторон равны.
- В любом вписанном четырехугольнике сумма противоположных углов равна 1800.
Для развития исследовательских умений учащимся целесообразно предлагать задания с элементами исследования: развить тему задачи, найти обощение, установить сходство, рассмотреть частный, предельный, вырожденный случай и т.д.[5] Использование программы "Живая геометрия" при решении таких задач позволяет значительно экономить учебное время за счет "динамичности" чертежа.
Рассмотрим пример. Учащимся предлагается следующая задача: "Две окружности пересекаются в точках М.и N. Через них проведены прямые, пересекающие окружности в точка А и В, С и D соответственно. Каково взаимное расположение прямых АС и ВD?"[5]
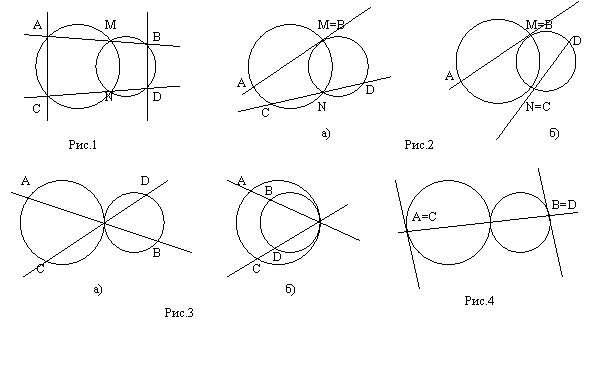
Каждый ученик с помощью инструментов "Живой геометрии" строит соответствующий чертеж (рис.1). Затем, легко и быстро изменяя размеры исходных объектов (окружностей), а следовательно, положение прямых АВ и СD, учащиеся рассматривают за короткое время множество аналогичных случаев и выдвигают гипотезу: "Прямые АС и ВD параллельны". Поиск основной идеи доказательства проводится коллективно под руководством учителя. (Основная идея доказательства: рассмотреть вписанные четырехугольники АМNC и NMBD.)
Далее ученикам предлагается, используя инструменты "Живой геометрии", рассмотреть возможные случаи взаимного расположения окружностей, окружностей и прямых из предложенной задачи:
- Одна или обе прямые АВ и СD касаются одной или разных окружностей, которые пересекаются (рис. 2, а, б).
- Данные окружности касаются внешним или внутренним образом (рис. 3, а, б).
- Данные окружности касаются внутренним или внешним образом, а пересекающие их прямые совпадают (рис. 4).
Свои выводы ученики записывают в текстовом окне на экране.
Таким образом, практика показала, что работа в компьютерной программе "Живая геометрия" не вызывает у учащихся 7 - 9 классов особых затруднений, а ее использование в процессе организации учебных исследований способствует:
- повышению качества усвоения учебного материала;
- уменьшению объема времени учебных исследований;
- развитию самостоятельности ученика;
- повышению качества учебных исследований;
- развитию интереса к экспериментальной и исследовательской деятельности.
СПИСОК ЛИТЕРАТУРЫ
- Баранова Е.В. Методические основы использования учебных исследований при обучении геометрии в основной школе: дис. ... канд. пед. наук. 13.00.02. - Саранск: АГПИ им. А.П. Гайдара, 1999 - 163 с.
- Геометрия, 7-9: Учеб. для общеобразоват. учреждений /Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдина. - М.: Просвещение, 2002. -384 с.
- Далингер В.А. Обучение учащихся доказательству теорем: Учеб. пособие. - Омск: Издательство ОмГПУ, 2002. - 419 с.
- Никифорова М. Новые компьютерные технологии //Математика. - 2004. - №31. - С.28-30.
- Цукарь А.Я. Дидактические материалы по геометрии с элементами исследования для 8 класса. - М.: Просвещение, 1999. - 80 с.



