Микроскопические методы исследования структурных фазовых переходов (СФП), показали, что мягкая мода прекращает свое смягчение и возникает узкий центральный пик, свидетельствующий о появлении переходной области и появлении ближнего порядка, проявляющегося в кластерах. Поэтому представляется весьма актуальным аналитическое описание СФП с образованием кластеров новой структуры.
Предлагается модель 
описания структурных фазовых переходов первого рода близких ко второму роду с помощью гамильтониана связанных ангармонических осцилляторов:
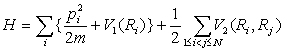(1)
в поле несимметричного одночастичного двухъямного потенциала:
. (2)
В зависимости от соотношения параметров данный потенциал может принимать симметричную форму и описывать непрерывный СФП или асимметричный и тогда, описывать СФП первого рода близких ко второму. Парный потенциал с силовыми константанами определяет взаимодействие активных при СФП атомов в соседних ячейках.
Гамильтониан (1) описывает «быстрые» степени свободы, характеризующие движения частиц в фононных модах и «медленные» степени свободы, которые проявляются в кластерах. Для их описания используется формула:
, 
,
где li - среднее равновесное положение ячейки, которое при фазовом переходе зависит от температуры и может быть вычислено как для метастабильной фазы в низкотемпературной области, так и в стабильной фазе в высокотемпературной области.
В случае, если энергия вибрационного движения атома меньше энергии одночастичного барьера, имеем низкотемпературную фазы. Атомы активные при фазовом переходе располагаются в более глубоком минимуме. В функции распределения равновесных положений атомов, имеется один острый пик, который указывает, что атомы находятся в низкотемпературной фазе и одинаково смещены в двухямном потенциале.
При увеличении температуры становится возможным заполнение другой ямы, что означает появление кластеров другой фазы в старой фазе и тогда имеем метастабильную фазу. При дальнейшем увеличении температуры энергия атомов увеличивается, и при переходе в критической точке покидают минимум и переходят в стабильную фазу. Функция распределения равновесных положений имеет один пик с центром в нуле и это означает, что частицы в высокотемпературной фазе находятся выше горба двухямного потенциала. При переходе из низкотемпературной фазы в стабильную в критической точке происходит скачек температурной зависимости среднего равновесного положения.
Гамильтониан (1) приближенно можно представить в виде суммы двух эффективных гамильтонианов для нелинейных возбуждений типа доменных стенок Нк и фононов Нф. с коэффициентами перенормировки, учитывающие кинк-фононное взаимодействие. Обоснованием разделения переменных в (1) является большая разница для характерных времен фононных и кинковых возбуждений системы 
.
В модели 
параметром порядка является среднее смещение атома из своего положения в узле решетки. Поведение параметра порядка с изменением температуры имеет характерный вид для фазовых переходов первого рода близких ко второму роду.
В фононном спектре «мягкой» моды метастабильной фазы имеется сдвиг относительно спектра фононов в стабильной фазе за счёт кластеров с различной симметрией, а квадрат её частоты испытывает типичный для СФП первого рода скачёк при температуре СФП.
Аналитический расчет теплоемкости дает типичную для теории Ландау и теории среднего поля картину скачков теплоемкости для разных фаз, и частично учитывает вклад флуктуаций параметра порядка вблизи температуры перехода и дает слабую λ-зависимость теплоемкости.
Для описания кинковой подсистемы на основе гамильтониана (1) получено уравнение Эйлера-Лагранжа, которое дает солитоноподобное решение. Наличие отрицательных значений энергии солитонов указывает на энергетическую выгодность системе образовывать солитоны в этой области температур.
Кинковая подсистема является ответственной за сдвиг фононных частот в усредненной решетке с кластерами разной фазы и за квазиупругий центральный пик в законе рассеяния, связанный с рассеянием излучения на стенках кластеров вблизи СФП.