ГЕРТ-сети относятся к классу стохастических сетей, построенных на направленном графе G(N, A), каждая дуга a ∈ A - некоторая «работа», а узел n ∈ N - это состояние. [3; 4] Выполнение ГЕРТ-сети (построение множества реализаций) не зависит от предыдущего состояния сети.
В модифицированной ГЕРТ-сети (далее МГ-сеть) указанное выше требование заменено условием «вычислимости» вероятности перехода по всем дугам после активации узла, из которого они выходят.
Реализацией МГ-сети будем называть последовательность активаций узлов от источника к стоку.
МГ-сеть называется вычисленной, если построено множество всех (или наиболее вероятных) ее реализаций.
Для построения реализаций МГ-сети используется алгоритм обхода графа сети с его стоков к источнику с последующим расчетом характеристик узлов полученного пути. Данный алгоритм основан на базе алгоритма обратного обхода графа в глубину. Будем называть его обратным алгоритмом расчета стохастической МГ-сети. [2]
Использование алгоритма обратного обхода графа сети обусловлено следующим условием: для каждого узла ni∈N с AND- или IOR-входом существует один и только один узел nj ∈N, являющийся стохастическим источником узла ni; узел nj имеет детерминированный выход; допускается существование пути с началом в узле nj таким, что узел ni не принадлежит данному пути.
Однако существует достаточно большой класс задач[1; 2; 3], для которых указанное выше условие можно заменить более жестким: для каждого узла ni∈N с AND- или IOR-входом существует один и только один узел nj ∈ N, являющийся стохастическим источником ni; узел nj имеет детерминированный выход; все пути с началом в nj, сходятся в узле ni.
Данное ограничение позволяет построить алгоритм расчета МГ-сети, основанный на алгоритме прямого обхода графа в глубину, в котором расчет каждой реализации частично заменяется копированием уже рассчитанных результатов. Будем называть его прямым алгоритмом расчета стохастической МГ-сети. Продемонстрируем работу алгоритмов на примере трех сетей.
Обозначения.

Время перехода на следующий доступный узел не существенно (пунктирная стрелка).
Время расчета функции распределения времени активации узла имеет порядок M2, где M - количество точек аппроксимации функций распределения суммируемых случайных величин. Будем оценивать время по формуле k1*M2.
Время копирования построенного пути имеет порядок M*(K-1), где K - количество узлов построенного пути. Будем оценивать время по формуле k2*M*(K-1).
Сеть 1:
|
Обратный алгоритмом расчета МГ-сети |
Прямой алгоритмом расчета МГ-сети |
|
Время расчета: 2*k1*M2 |
Время расчета: 2*k1*M2 |
Сеть 2:
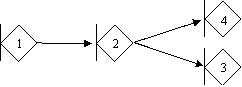
|
Обратный алгоритмом расчета МГ-сети |
Прямой алгоритмом расчета МГ-сети |
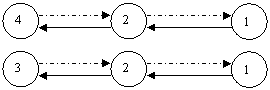 |
 |
|
Время расчета: 4*k1*M2 |
Время расчета: k2*M+3*k1*M2 |
Сеть 3:
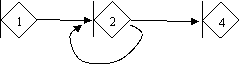
Для сети 3 выберем максимальное число активаций узла 2, равное трем (L=3). Данное условие необходимо для ограничения количества реализаций сети.
|
Обратный алгоритмом расчета МГ-сети |
Прямой алгоритмом расчета МГ-сети |
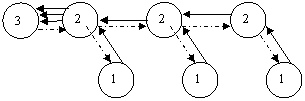 |
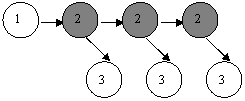 |
|
Время расчета: (k1*M2)*(L2 + L + 2)/2 |
Время расчета: |
Выводы:
Алгоритм на базе прямого обхода графа всегда не хуже по производительности алгоритма на базе обратного графа. Однако, как уже отмечалось выше, область его применения уже. Выбор алгоритма определяется структурой сети, следовательно, он осуществим на этапе построения сети.
СПИСОК ЛИТЕРАТУРЫ
- Дегтерев А.С., Письман Д.М. GERT-сетевой анализ времени выполнения задачи на неспециализированном гетерогенном кластере. Фундаментальные исследования. 4/2005. ISSN 1681-7494. с. 79-80.
- Лебедев В. А., Трохов Н. Н., Царев Р. Ю. Параллельные процессы обработки информации в управляющих системах. - Красноярск, НИИ СУВПТ, 2001. с. 120-133.
- Письман Д.М., Шабалин С.А. Алгоритм расчета модифицированной ГЕРТ-сети. Успехи современного естествознания. 11/2005. ISSN 1681-7494. с. 36-37
- Филлипс Д., Гарсиа-Диас А. Методы анализа сетей.-М.: Мир, 1984. с. 387-411.
- Neumann K. Stochastic Project Networks. Temporal Analysis, Scheduling and Cost Minimization. Springer-Verlag. p. 37-115.



