Проблема исследований: Параллельная обработка данных в вычислительных трактах по модулям системы полиномиальной системы классов вычетов (ПСКВ) может служить базисом в реализации процедур коррекции ошибок. Разработанные алгоритмы поиска и исправления ошибок позволяют повысить эффективность функционирования спецпроцессоров (СП) ПСКВ.
Решение проблемы исследований: При решении многих практических задач цифровой обработки сигналов (ЦОС) необходимо осуществлять ортогональные преобразования. Известно, что использование математической модели ЦОС поля комплексных чисел характеризуется целым рядом недостатков, основные из которых приведены в работе [1]. В работах [2,3] предложена реализация ортогональных преобразований сигналов в полиномиальной системе классов вычетов (ПСКВ) расширенных полей Галуа GF (2v). Основным достоинством такой непозиционной арифметики является возможность организации параллельных вычислений и, следовательно, значительное повышение быстродействия вычислительного устройства ЦОС. Кроме того, применение ПСКВ позволяет сократить аппаратурные затраты необходимы на реализацию вычислительной системы [3].
Если выбрать k из n оснований ПСКВ (k < n ), то это позволит осуществить разбиение полного диапазона 
расширенного поля Галуа 
на два непересекающихся подмножества. Первое подмножество называется рабочим диапазоном и определяется выражением
, (1)
Многочлен A(z) с коэффициентами из поля GF(p) будет считаться разрешенным в том и только том случае, если он принадлежит Рраб(z). Второе подмножество, определяемое произведением r=n-k контрольных оснований,
, (2)
задает совокупность запрещенных комбинаций. Если A(z) является элементом второго подмножества, то считается, что данная комбинация содержит ошибку. Таким образом, местоположение полинома A(z) относительно двух данных подмножеств позволяет однозначно определить, является ли комбинация 
разрешенной, или содержит ошибочные символы.
Особое место среди методов поиска и коррекции ошибок в процессе вычислений отводится интервальному номеру полинома согласно выражения:
. (3)
В работе [4] представлено устройство, осуществляющее обнаружение и коррекцию ошибки в модулярном коде на основе вычисления интервального номера. В основу данного алгоритма положен алгоритм
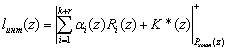, (4)
где ранг определяется выражением
. (5)
Если lинт(z)= 0, то исходный полином А(z) лежит внутри рабочего диапазона и не является запрещенным. В противном случае А(z) - ошибочная комбинация.
Анализ выражения (4) показывает, что применение составного модуля Ркоит(z), с точки зрения аппаратурных затрат, является не самым оптимальным. Использование изоморфизма, порожденного КТО, позволяет перейти от одномерной обработки к многомерной. Приравнивая соответствующие значения Рконт(z) и оснований 
, получаем r преобразований
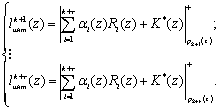(6)
Основным недостатком предложенного алгоритма является вычисление ранга K(z). Решить данную проблему можно за счёт модификации алгоритма (6). В основу данной модификации положено свойство - отсутствие переноса единицы из младшего разряда в старший при выполнении арифметической операции сложения двух операндов в расширенных полях Галуа GF (2v). Таким образом, величина ранга K*(z) безизбыточной системы ПСКВ p1(z),..., pk(z) определяется значением и , и никоим образом не зависит от переполнения диапазона Pраб(z). Тогда (6) примет вид:
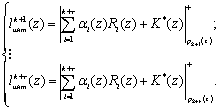(7)
Таким образом, применение выражения (7) позволяет осуществить вычисление интервального номера lинт(z) на основе только модульных процедур.
Выводы: В ходе выполнения работы был разработан алгоритм вычисления lинт(z), характеризующийся минимальными схемными затратами. Кроме того, проведенные исследования показали, что с увеличением разрядности вычислительного устройства эффективность алгоритма (24) возрастает.
СПИСОК ЛИТЕРАТУРЫ
- Вариченко Л.В. Абстрактные алгебраические системы и цифровая обработка сигналов. - Киев: Наука думка, 1986. -.247 с.
- Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Бережной В.В. Математическая модель нейронных сетей для исследования ортогональных преобразований в расширенных полях Галуа/Нейрокомпьютеры: разработка, применение. №6, 2003. с.61-68.
- Калмыков И.А. Математические модели нейросетевых отказоустойчивых вычислительных средств, функционирующих в полиномиальной системе классов вычетов/Под ред. Н.И. Червякова. - М.: ФИЗМАТЛИТ, 2005. - 276 с.
- Калмыков И.А. Устройство для вычисления сумм парных произведений/Патент № 2012041 /Открытия. Изобретения. - 1994. Бюл. № 8.