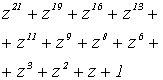Применение полиномиальной системы классов вычетов (ПСКВ), в которой в качестве оснований выбираются минимальные многочлены pi(z) поля GF(pv), позволяет полином A(z), удовлетворяющий условию:
, (1)
представить в виде:
, (2)
где 
, 
.
поля GF(pv) на два подмножества, первое из которых называется рабочим диапазоном
, (3)
а второе подмножество GF(pv), определяемое произведением r=n-k контрольных оснований:
, (4)
задает совокупность запрещенных комбинаций. Многочлен A(z) будет считаться разрешенным в том и только том случае, если он является элементом нулевого интервала полного диапазона , то есть 
.
Для определения местоположения 
используется метод нулевизации, заключающейся в переходе от исходного полинома к полиному вида:
, (5)
при помощи последовательных преобразований, при которых не имеет место ни один выход за пределы рабочего диапазона системы. Нулевизация заключается в последовательном вычитании из исходного полинома, представленного в модулярном коде, констант нулевизации, с целью получения
. (6)
Если в результате выполнения процедуры нулевизации будет получен нулевой результат, то это свидетельствует, что комбинация A(z) не содержит ошибок. В противном случае - модулярный код A(z) - содержит ошибки.
Повысить скорость выполнения процедуры нулевизации можно за счет модификации констант нулевизации Mi(z). Оставляя неизменным условие невыхода константы нулевизации Mi(z) за пределы рабочего диапазона 
, возьмем в качестве последних значения произведение остатков рабочих оснований на величину ортогональных базисов безизбыточной системы оснований
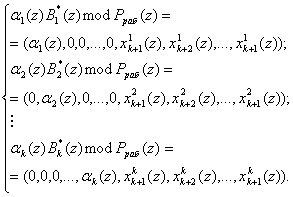(7)
где Bi*(z) - ортогональный базис, безизбыточной системы оснований; i=1,2,...,k.
Тогда если положить условие, что , где , то полином 
согласно китайской теореме об остатках (КТО) можно представить в виде
. (8)
Каждое слагаемое выражения (9) представляет собой:
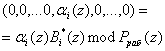, (9)
Подставим выражения (8) в равенство (10). Получаем:
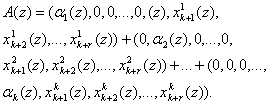(10)
Разность полинома A(z) и модифицированных констант нулевизации Mi(z), i=1, 2,..., k, псевдоортогональных форм, задаёт величину нормированного следа полинома
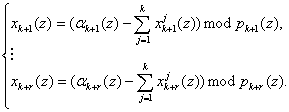(11)
Рассмотрим ПСКВ, определяемую в поле GF(25). В таблице 1 помещены значения рабочих и контрольных оснований ПСКВ, а также динамический диапазон.
Таблица 1. Основания и динамический диапазон поля GF(25)
|
Основания ПСКВ |
Рабочий диапазон ПСКВ |
|
|
Рабочие |
Контрольные |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определим все значения произведений степеней zj на ортогональные базисы Bi*(z), учитывая невозможность выхода за пределы рабочего диапазона 
. Полученные значения модифицированных констант нулевизации представлены в таблице 2.
Таблица 2. Константы нулевизации для поля GF(25)
|
|
α1(z) |
α2(z) |
α3(z) |
α4(z) |
α5(z) |
α6(z) |
α7(z) |
|
|
1 |
0 |
0 |
0 |
0 |
z2 |
z |
|
|
0 |
1 |
0 |
0 |
0 |
1 |
1 |
|
|
0 |
z |
0 |
0 |
0 |
z |
z |
|
|
0 |
z2 |
0 |
0 |
0 |
z2 |
z2 |
|
|
0 |
z3 |
0 |
0 |
0 |
z3 |
z3 |
|
|
0 |
z4 |
0 |
0 |
0 |
z4 |
z4 |
|
|
0 |
0 |
1 |
0 |
0 |
z4+z |
z4+1 |
|
|
0 |
0 |
z |
0 |
0 |
z3+z2+1 |
z3+z+1 |
|
|
0 |
0 |
z2 |
0 |
0 |
z4+z3+z |
z4+z2+z |
|
|
0 |
0 |
z3 |
0 |
0 |
z4+1 |
z+1 |
|
|
0 |
0 |
z4 |
0 |
0 |
z2+z+1 |
z2+z |
|
|
0 |
0 |
0 |
1 |
0 |
z2 |
z+1 |
|
|
0 |
0 |
0 |
z |
0 |
z3 |
z2+z |
|
|
0 |
0 |
0 |
z2 |
0 |
z4+z3+z2 |
z3+z |
|
|
0 |
0 |
0 |
z3 |
0 |
z4+1 |
z4+z2 |
|
|
0 |
0 |
0 |
z4 |
0 |
z3+z+1 |
z3+z2+1 |
|
|
0 |
0 |
0 |
0 |
1 |
z4+z |
z4 |
|
|
0 |
0 |
0 |
0 |
z |
1 |
z3+z2+z+1 |
|
|
0 |
0 |
0 |
0 |
z2 |
z |
z4+z3+z2+z |
|
|
0 |
0 |
0 |
0 |
z3 |
z2 |
z4+z+1 |
|
|
0 |
0 |
0 |
0 |
z4 |
z3 |
z3+1 |
Пусть в поле GF(25) задан полином A(z)=z6+z5+z4+1. Данный полином принадлежит Рраб(z). Представим его в модулярном коде
A(z)=z6+z5+z4+1= (0, z3+z, z4+z3+z2+z+1, z2+z+1, z3+z+1, z4+z3+z2+z, 0).
Проведем процедуру нулевизации.
1 этап
A(z) = (0, z3+z, z4+z3+z2+z+1, z2+z+1, z3+z+1, z4+z3+z2+z, 0)
М2(z)=(0, z3+z, 0, 0, 0, z3+z, z3+z)
A2(z)=(0, 0, z4+z3+z2+z+1, z2+z+1, z3+z+1, z4+z2, z3+z)
2 этап
A2(z) =(0, 0, z4+z3+z2+z+1, z2+z+1, z3+z+1, z4+z2, z3+z)
М3(z)=(0, 0, z4+z3+z2+z+1, 0, 0, z4+z+1, z3+1)
A3(z)=(0, 0, 0, z2+z+1, z3+z+1, z2+z+1, z+1)
3 этап
A3(z) =(0, 0, 0, z2+z+1, z3+z+1, z2+z+1, z+1)
М4(z)=(0, 0, 0, z2+z+1, 0, z4, z3+z2+z+1)
A4(z)=(0, 0, 0, 0, z3+z+1, z4+z2+z+1, z3+z2)
4 этап
A4(z) =(0, 0, 0, 0, z3+z+1, z4+z2+z+1, z3+z2)
М5(z)=(0, 0, 0, 0, z3+z+1, z4+z2+z+1, z3+z2)
A5(z)=(0, 0, 0, 0, 0, 0, 0)
Таким образом, полином A(z) не содержит ошибки.
Пусть ошибка произошла по 1 основанию
A*(z)= (1, z3+z, z4+z3+z2+z+1, z2+z+1, z3+z+1, z4+z3+z2+z, 0).
В результате проведения процедуры нулевизации получен результат: A5(z)=(0, 0, 0, 0, 0, z2, z), что свидетельствует о наличии ошибки в модулярном коде.
СПИСОК ЛИТЕРАТУРЫ
- Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Бережной В.В. Математическая модель нейронных сетей для исследования ортогональных преобразований в расширенных полях Галуа/Нейрокомпьютеры: разработка, применение. №6, 2003. с.61-68.
- Калмыков И.А. Математические модели нейросетевых отказоустойчивых вычислительных средств, функционирующих в полиномиальной системе классов вычетов/Под ред. Н.И. Червякова. - М.: ФИЗМАТЛИТ, 2005. - 276 с.