Основным этапом большинства алгоритмов обнаружения и коррекции ошибок в модулярных кодах является процедура вычисления позиционной характеристики. Реализация подхода предполагает использование некоторого функционального отношения, однозначно отражающего множество значений модульных характеристик во множество рассматриваемых ошибок E.
Широкое распространение в модулярных кодовых конструкциях получили такие позиционные характеристики как ранг, след, ядро числа, нормированное ядро числа и квазиранг числа [1]. Следует отметить, что большинство способов определения позиционных характеристик кодов класса вычетов обладают довольно высоким уровнем параллелизма и могут быть эффективно реализованы на нейросетевом базисе [2].
Особое место среди позиционных характеристик модулярных кодов полиномиальной системы класса вычетов (ПСКВ) занимает интервальный номер полинома 
[2,3]. Процесс определения интервала полинома 
сводится к выполнению операции:
. (1)
где 
- рабочий диапазон, 
; - основание ПСКВ.
Исправление ошибки в модулярном коде на основе позиционной характеристики интервал происходит согласно следующему алгоритму.
Выразим полином через его остатки 
в виде
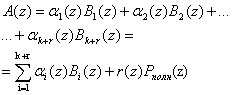(2)
где r(z)- ранг полинома A(z).
Подставив в равенство (1) последнее выражение, и упрощая, получаем
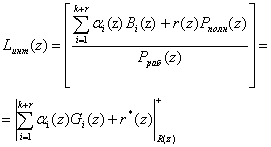, (3)
где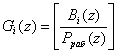 
; 
- ранг безизбыточной системы ПСКВ, определяемой основаниями 
; 
.
Таким образом, определение интервального номера 
полинома A(z) сводится к выполнению модульных операций в ПСКВ поля 
.
Если 
, то исходное A(z) лежит внутри рабочего диапазона Pраб и не является запрещенным. В противном случае A(z) - ошибочная комбинация, а Lинт указывает местоположение и глубину ошибки 
по i-му основанию.
Основным недостатком предложенного метода является необходимость реализации немодульной процедуры - вычисления ранга числа A(z), что, в конечном счете, снижает скорость работы устройства и его надежность [4]. Для решения данной проблемы целесообразно воспользоваться нормированным следом Sk+1, l=1,2,,...,r. Исходя из условия подобия ортогональных базисов рабочих оснований в избыточной Bi и безызбыточной 
системах 
, 
и делимости без остатка ортогональных базисов контрольных оснований на Pраб, т.е. 
, 
выражение (1) принимает вид:
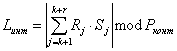, (4)
где 
; 
; 
- нормированный след по j-ому основанию.
Обобщая свойства системы остаточных классов на ПСКВ, получаем выражение для вычисления интервального полинома
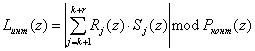, (5)
Значение полинома 
позволяет однозначно определять местоположение полинома 
относительно Pраб(z). Если 
, то полином A(z) лежит внутри рабочего диапазона и не содержит ошибки. В противном случае - полином A(z) является ошибочным. Так, для полинома 
значение интервального полинома согласно (3) составит
,
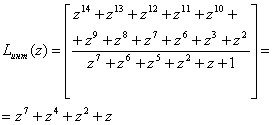свидетельствует о наличии ошибки в исходной комбинации A(z).
Используем выражение (5) для определения интервального полинома:
; 
;
; 
;
.
Тогда
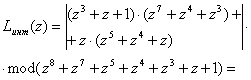
Таким образом, применение выражения (5) позволяет осуществить вычисление интервального полинома Lинт(z) на основе только модульных процедур, используя значения нормированного следа 
, l=1,2,...,r.
В работе [4] представлена структура устройства вычисления интервального полинома, реализованного в нейросетевом логическом базисе, для поля GF(24). Применение разработанного алгоритма позволяет исправить 100% однократных ошибок и свыше 95% двукратных ошибок. Полученные результаты имеют важное практическое значение, так как позволяют строить отказоустойчивые параллельные вычислительные системы.
СПИСОК ЛИТЕРАТУРЫ
- Акушский И.Я., Юдицкий Д.И. Машинная арифметика в остаточных классах. - М.: Сов. радио, 1968.- 440 с.
- Калмыков И.А. Математические модели нейросетевых отказоустойчивых вычислительных средств, функционирующих в полиномиальной системе классов вычетов/Под ред. Н.И. Червякова. - М.: ФИЗМАТЛИТ, 2005. - 276 с.
- Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Бережной В.В. Математическая модель нейронной сети для коррекции ошибок в непозиционном коде расширенного поля Галуа/Нейрокомпьютеры: разработка, применение. №8-9, 2003. С. 10-16.
- Калмыков И.А., Емельяненко С.В., Лисицын А.В. Устройство для вычисления сумм парных произведений в полиномиальной системе классов вычетов. Решение о выдаче патента (№ 2004101990/09(001852). Приоритет от 22.01.2004.