Основным методом случайного поиска глобального экстремума многомерных функций является мультистарт [1, 2]. При его использовании из множества X случайно или детерминировано выбирается некоторое подмножество из N точек. На каждом i-том подмножестве из случайной начальной точки Ui делается локальный спуск в ближайший минимум Ui* любым локальным методом поиска. За глобальный минимум U** принимается тот, для которого показатель качества минимален, т.е.:
.
Очевидно, что при 
вероятность того, что 
является положением глобального минимума, стремится к единице, т. е.
.
При конечном N вероятность потери глобального экстремума, т. е. 
, не равна нулю.
Мультистарт - это обобщенный подход: большинство эффективных методов глобальной оптимизации основано на идее метода мультистарта - запуска стандартных локальных алгоритмов из множества точек, равномерно распределенных на множестве X. Таким образом, метод мультистарта можно назвать прототипом таких методов.
Адаптивный набросовый алгоритм [3, 4] связан с адаптивным изменением плотности распределения наброса (случайное распределение пробных состояний объекта). Пусть 
- плотность распределения, параметры которого определяются вектором W, равным математическому ожиданию случайного вектора U:
,
и σ - некоторой скалярной мерой рассеяния этого распределения (типа среднеквадратичного отклонения), такой, что при σ = 0 распределение вырождается в δ-функцию, и имеем U=W, а с увеличением σ область наброса расширяется пропорциональна σ по всем направлениям пространства {U}. Алгоритм поиска заключается в генерировании последовательности случайных точек U1,..., UN,... и выборе точки с наименьшим значением показателя качества:
.
При этом параметры W и σ распределения адаптируются, например, следующим образом:
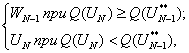
т.е. WN является лучшей из всех предыдущих точек, и
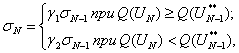
где параметры 
и 
могут выбираться исходя из различных соображений.
В случае <1 и >1, т. е. при расширении зоны поиска с каждой удачей и сужении - с неудачей, получаем локализирующийся алгоритм, который стремится «стянуть» наброс вокруг лучшей точки. Темп такого стягивания определяет степень глобальности алгоритма. Если стягивание происходит быстро, то, очевидно, будет найден ближайший локальный экстремум; если же медленно, то шансы найти экстремум лучше ближайшего локального повышаются.
В случае γ≈1 вероятность отыскания глобального экстремума, при N →∞ стремится к единице (при этом еще необходимо, чтобы 
для любой точки, т. е. чтобы плотность вероятности появления любой допустимой точки не была равна нулю).
Возможен и иной подход к выбору параметров и . Если логику адаптации как бы «вывернуть наизнанку», т.е. положить >1, а <1, то получим несходящуюся процедуру, которая расширяет зону поиска при неулучшении и сужает ее при отыскании лучших точек. Оба подхода обладают своими достоинствами и недостатками. Применение их связанно с конкретными свойствами объекта.
Наиболее простой алгоритм поиска экстремума методом сканирования [5, 6] ("поиск на сетке переменных") заключается в том, что по каждой независимой переменной задаются приращения в соответствующем порядке, обеспечивающем "заполнение" всей исследуемой области равномерной и достаточно густой сеткой. Из значений функции в узлах сетки выбирается оптимальное значение.
Объем вычислений при использовании метода сканирования можно оценить по следующей формуле:
,
где D - точность определения экстремума, n - количество независимых переменных.
Модификации метода сканирования применяются в основном для сокращения объема вычислений. При сканировании с переменным шагом вначале задается достаточно большой шаг (DU > e) и выполняется "грубый" поиск, который локализует область существования глобального экстремума (P). После того, как область определена, производится поиск с меньшим шагом только в пределах найденной области (s). Можно организовать ряд таких процедур последовательного уточнения положения оптимума (s).
При использовании данного алгоритма объем вычислений существенно сокращается и может быть определен по формуле:
,
где r - число этапов уточнения поиска, на котором шаг уменьшался в К раз, n - число независимых переменных; D - точность определения экстремума.
Начальный шаг сетки переменных в данном случае определяется формулой:
.
Методы случайного поиска глобальных экстремумов многомерных функций дают высокую вероятность достижения поставленной цели.
СПИСОК ЛИТЕРАТУРЫ
- Жиглявский А.А., Жилинскас А.Г. Методы поиска глобального экстремума. М.: Наука, 1991.
- Орлянская И.В. Современные подходы к построению методов глобальной оптимизации, МГУ, факультет ВМиК.
- Растригин Л.А.. Адаптация сложных систем. Рига «Зинатне» 1981.
- Справочник по теории автоматического управления. 1987 г. «Наука».
- Сидоров Б.Н., Никулин А.М. Методы безусловной оптимизации функции одной переменной. Москва, 1999 г.
- http://www.opu.odessa.ua/konsp/MMXTP/RAZDEL5/glava576.htm.