На k-м этапе градиентных методов переход из точки Xk в точку Xk+1 описывается соотношением 
, где 
- величина шага, Sk - вектор в направлении 
.
Способ определения и Sk на каждой итерации связан с особенностями применяемого метода. Обычно выбор осуществляется путем решения задачи минимизации целевой функции (f(X)) в направлении Sk. Поэтому при реализации градиентных методов необходимо использовать эффективные алгоритмы одномерной минимизации.
В основе простейшего градиентного метода [2] лежит следующая итерационная модификация формулы:
, где 
- заданный положительный коэффициент; 
- градиент целевой функции первого порядка.
Недостатки:
- необходимость выбора подходящего значения ;
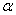- медленная сходимость к точке минимума ввиду малости 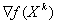в окрестности этой точки.
Идея метода наискорейшего спуска проста [1, 2]: градиент целевой функции f(X) в любой точке есть вектор в направлении наибольшего возрастания значения функции. Следовательно, антиградиент будет направлен в сторону наибольшего убывания функции и является направлением наискорейшего спуска. Антиградиент (и градиент) ортогонален поверхности уровня f(X) в точке X. Если в ввести направление 
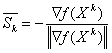, то это будет направление наискорейшего спуска в точке Xk.
Тогда формула перехода из Xk в Xk+1:
.
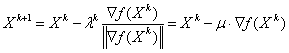Антиградиент дает только направление спуска, но не величину шага. В общем случае один шаг не дает точку минимума, поэтому процедура спуска должна применяться несколько раз. В точке минимума все компоненты градиента равны нулю
Направление поиска, соответствующее наискорейшему спуску, связано с линейной аппроксимацией целевой функции. Методы, использующие вторые производные, возникли из квадратичной аппроксимации целевой функции. При разложении функции в ряд Тейлора отбрасываются члены третьего и более высоких порядков:
,
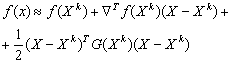где G(Xk) - матрица Гессе.
Минимум правой части (если он существует) достигается там же, где и минимум квадратичной формы. Тогда формула для определения направления поиска 
:
.
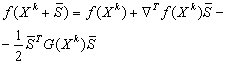Минимум достигается при 
.
Алгоритм оптимизации, в котором направление поиска определяется из этого соотношения, называется методом Ньютона [1, 4], а направление - ньютоновским направлением.
В задачах поиска минимума произвольной квадратичной функции с положительной матрицей вторых производных метод Ньютона дает решение за одну итерацию независимо от выбора начальной точки.
Идея алгоритма Пауэлла [3] состоит в том, что на каждом этапе поиска определяется минимум квадратичной функции, которой аппроксимируется целевая функция, вдоль каждого из сопряженных ко всем предыдущим. Затем выбирается новая система направлений с использованием результатов поиска и утверждения.
Процедура Пауэлла сходится к точке, в которой градиент равен нулю, если f(X) - строго выпуклая функция. Эта точка является локальным экстремумом. Метод очень чувствителен к способу построения сопряженных направления и поэтому зависит от точности используемого одномерного поиска.
Алгоритм метода сопряженных направлений Пауэлла заключается в следующем.
Шаг 1. Задать начальную точку xo и систему N линейно независимых направлений si ; целесообразно принять si = ei, i=1,2,...,N.
Шаг 2. Минимизировать при последовательном движении по N+1 направлениям; при этом полученная ранее точка минимума берется в качестве исходной, а направление sN используется как при первом, так и при последнем поиске.
Шаг 3. Определить новое сопряженное направление с помощью обобщенного свойства параллельного подпространства.
Шаг 4. Заменить s1 на s2 и так далее. Заменить sN сопряженным направлением. Перейти к шагу 2.
Для применения метода на практике его необходимо дополнить процедурами проверки сходимости и линейной независимости системы направлений. Если целевая функция квадратична и обладает минимумом, то точка минимума находится в результате реализации N циклов, включающих шаги 2-4. Здесь N - число переменных. Если же функция f(X) не является квадратичной, то требуется более чем N циклов.
СПИСОК ЛИТЕРАТУРЫ
- http://m-16rulez.narod.ru/Ucheba/MOP/Bo4.doc.
- Иркитова М.А. Методы безусловной оптимизации, 2001.
- http://m-16rulez.narod.ru/Ucheba/MOP/Bo3.doc.
- Горелик В.А. Математическое программирование.