Основным интервальным методом поиска глобального экстремума многомерной функции является метод ветвей и границ [1, 2, 3, 5]. Метод начинает работу с определения нижней и верхней границ для исходной задачи. Если верхняя и нижняя границы совпадают, то полученный результат является оптимальным значением, и метод прекращает работу. Иначе, множество переменных разбивается на несколько собственных подмножеств, объединение которых совпадает с исходным множеством. Эти подзадачи становятся потомками исходной. Далее алгоритм применяется рекурсивно к каждой из подзадач, создавая дерево подзадач. Если оптимальное решение найдено для некоторой подзадачи, то оно является достижимым для исходной задачи (не обязательно оптимальным), но так как оно достижимо, его можно использовать для обрезания ветвей у исходного дерева. Процесс поиска продолжается до тех пор, пока каждая из подзадач не будет решена или выкинута или до тех пор, пока не будет достигнут заданный порог между лучшим из найденных решений и нижней границей f(x) для всех нерешенных задач.
Описание алгоритма:
Нулевой шаг - вычисление нижней границы ξ (G) множества решений G : ξ (G) = ξ (G(0)).
Если при этом удается найти такой план x0, что f(x0 ) = ξ (G(0)), то x0 - оптимальный план. Если оптимальный план x0 не найден, то некоторым способом разбивают множество G(0) на конечное число непересекающихся подмножеств 
, таких что 
и переходят к первой итерации.
Первая итерация - вычисляют оценки 
при 
. Если удается найти такой план x0, что 
и 
при , то x0 - оптимальный план. В противном случае для дальнейшего разбиения выбирают наиболее перспективное множество 
по следующему правилу:
.
Разбивают множество 
на несколько подмножеств 
. Еще не подвергавшиеся разбиению множества переобозначают 
и переходят ко второй итерации.
k-ая итерация - вычисляют оценки 
при 
. Если удается найти такой план x0, для которого 
для всех , то x0 - оптимальный план. Если же оптимальный план не найден, то снова выбирают наиболее перспективное множество 
такое, что 
.
Далее разбивают множество на несколько подмножеств и переходят к (k+1)-й итерации.
Суть работы метода Хансена [1, 4] заключается в последовательном удалении из начальной области подобластей, в которых не содержится глобальный минимум. Удаление происходит одним из ниже перечисленных способов:
- Удаляются подобласти, в которых градиент g функции f отличен от нуля.
- Удаляются подобласти, в которых
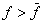, где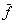 
- верхняя оценка глобального минимума. - Удаляются подобласти, в которых функция f невыпукла.
СПИСОК ЛИТЕРАТУРЫ
- Долгов Ю.Г. Метод глобальной оптимизации на основе метода ветвей и границ.
- Nemhauser G.L., Wolsey L.A. Integer combinatorial optimization. - New York: Wiley.
- Харчистов Б.Ф. Методы оптимизации. Учебное пособие. Таганрог 2004.
- Hansen E., Global Optimization Using Interval Analysis. - New York: Dekker, 1992.
- http://iasa.org.ua/iso.php?lang=rus&ch=4&sub=3.