Теория гиперустойчивости как прикладная задача математики нашла большое применение при решении задач синтеза дискретных адаптивных систем управления. Синтез, проводимый в рамках критерия гиперустойчивости, условно разбивается на ряд этапов, каждый из которых хорошо формализован и имеет самостоятельное решение [1].
Рассмотрим подробно задачу синтеза дискретной адаптивной системы управления непрерывным объектом, обладающим запаздываниями по состоянию и управлению. При решении данной задачи удобно воспользоваться результатами метода непрерывных моделей [2]. Согласно этому методу первоначально синтез рассматривается относительно непрерывной системы. В последствии, от полученных в непрерывном виде законов управления основного и дополнительного контуров осуществляется переход к их дискретному аналогу.
Пусть априорно неопределенный объект управления описывается следующими уравнениями пространства состояний:
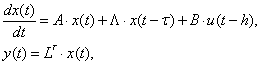 (1)
(1)
где ![]() ;
; ![]() ;
; ![]() ; m - порядок числителя передаточной функции объекта управления.
; m - порядок числителя передаточной функции объекта управления.
Скалярное управление сформируем следующим образом:
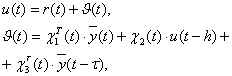 (2)
(2)
где r(t) - задающие воздействие; ![]() - отфильтрованный выходной сигнал объекта (1), получаемый с помощью фильтра вида
- отфильтрованный выходной сигнал объекта (1), получаемый с помощью фильтра вида
![]() , (3)
, (3)
где g(s), c(s) - гурвицевы полиномы степени n-1.
Для компенсации запаздывания и задания желаемой динамики процессов управления в систему вводится явно-неявный эталонный упредитель [3]
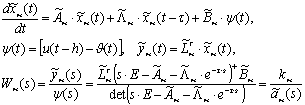 (4)
(4)
где ![]() ;
; ![]() ;
; ![]() - гурвицев квазиполином степени l.
- гурвицев квазиполином степени l.
При этом минимальной форме представления эталонного упредителя (4) будет соответствовать явная форма записи, порядок уравнений в которой, соразмерен порядку объекта (1) [4].
Вводя в рассмотрение сигнал ошибки, сформированный относительно соединения объект управления + фильтр и эталонный упредитель + фильтр
![]() (5)
(5)
где ![]() ,
, ![]() - переменные пространства состояния соответственно соединений «явный эталонный упредитель + фильтр» и «объект управления + фильтр», можно показать, что для системы (1)-(5) будет иметь место следующие эквивалентное математическое описание:
- переменные пространства состояния соответственно соединений «явный эталонный упредитель + фильтр» и «объект управления + фильтр», можно показать, что для системы (1)-(5) будет иметь место следующие эквивалентное математическое описание:
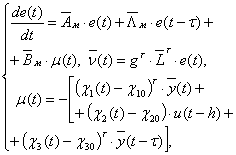 (6)
(6)
где ![]() - матрицы и вектор соответствующей размерности, записанные относительно последовательного соединения явного эталонного упредителя и фильтра.
- матрицы и вектор соответствующей размерности, записанные относительно последовательного соединения явного эталонного упредителя и фильтра.
Проблема гиперустойчивости эквивалентной системы (6) решается путем выполнения следующих двух условий:
во-первых: передаточная функция линейной стационарной части системы (6):
(7)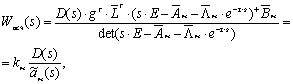
должна быть строго положительно-вещественная функция, где D(s) - специально-вводимый в систему гурвицев полином, степени l-1;
во-вторых: должно обеспечиваться выполнение интегрального неравенства В.М. Попова вида:
![]() ,(8)
,(8)
где ![]() ,
, ![]() - сигнал управления и обобщенный выход системы (6), расширенной с помощью дополнительно вводимого полинома D(s).
- сигнал управления и обобщенный выход системы (6), расширенной с помощью дополнительно вводимого полинома D(s).
Таким образом, первое условие гиперустойчивости системы (6) формирует требования относительно параметров эталонного упредителя и полинома D(s), и наиболее просто может быть разрешено при выполнении частотного неравенства вида
![]() . (9)
. (9)
Второе условие гиперустойчивости (8) помогает синтезировать алгоритмы самонастройки регулятора (2), которые в нашем случае будут иметь вид:
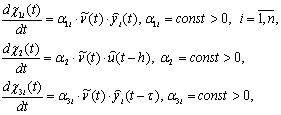 (10)
(10)
где ![]() и
и ![]() - расширенный сигнал выхода соединения «объект + фильтр» и расширенный сигнал управления.
- расширенный сигнал выхода соединения «объект + фильтр» и расширенный сигнал управления.
Согласно критерию гиперустойчивости при выполнении условий (8), (9) гарантируется не только устойчивость эквивалентно преобразованной системы, но и устойчивость исходной системы (1)-(4), (7), (10) - что и требовалось получить.
Если теперь от синтезированной непрерывной системы управления перейти к ее дискретному аналогу, то окончательно получим следующую гибридную адаптивную систему управления непрерывным объектом (1):
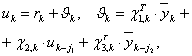 (11)
(11)
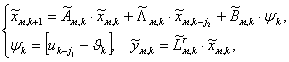 (12)
(12)
![]() , (13)
, (13)
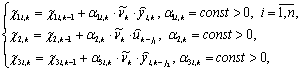 (14)
(14)
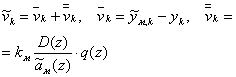 , (15)
, (15)
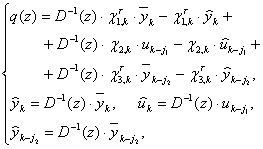 (16)
(16)
где z - переменная Z-преобразования; ![]() - дискретный аналог времени;
- дискретный аналог времени; ![]() - шаг дискретизации; k=0,1,2,.... - номер шага.
- шаг дискретизации; k=0,1,2,.... - номер шага.
Полученная таким образом дискретная система адаптивного управления (1), (11)-(16) может быть использована при управлении объектами, обладающими запаздываниями по состоянию и управлению. Предлагаемый в работе подход к решению проблемы гиперустойчивости позволяет получить систему адаптивного управления минимальной структурной сложности.
СПИСОК ЛИТЕРАТУРЫ
- Landau I.D. Adaptive control systems: the model reference approach. - N.Y.: Marsel Dekker, 1979. 406 p.
- Деревицкий Д. П., Фрадков А. Л. Прикладная теория дискретных адаптивных систем. М.: Наука. 1981.
- Еремин Е.Л. Построение адаптивных систем с запаздыванием по управлению на основе эталонного упредителя //Информатика и системы управления. 2005. № 1(9). С. 122-128.
- Еремин Е.Л. Робастные алгоритмы нестационарных систем управления с явно-неявной эталонной моделью //Электронный журнал «Дифференциальные уравнения и процессы управления», №3, 2001, http://www.neva.ru/journal.



