Введение
Одним из видов задач параметрической оптимизации является задача Марковица [1], который впервые предложил математическую формализацию задачи нахождения оптимальной структуры портфеля ценных бумаг в 1951 году, за что позднее был удостоен Нобелевской премии по экономике [2-4]. Существует две постановки задачи оптимизации портфеля ценных бумаг по максимизации доходности портфеля при заданном уровне риска, и минимизации риска портфеля при заданной доходности [5].
Цель исследования – разработка генетического алгоритма для поиска квази-оптимальных решений задачи максимизации доходности портфеля в задаче Марковица, и адаптации генетических операторов к этой задаче.
Материалы и методы исследования
В процессе исследования использовались статистический анализ, имитационное моделирование и системный анализ. Для решения поставленных задач использовались методы генетических алгоритмов, представляющие собой класс методов искусственного интеллекта. Данными для исследования являются ценовая динамика ценных бумаг из открытых источников Мосбиржи.
Результаты исследования и их обсуждение
Постановка задачи Марковица, об оптимизации портфеля ценных бумаг, в контексте максимизации доходности портфеля при заданном уровне риска, постановка которой отражена в формуле 1.
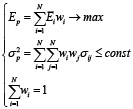 , (1)
, (1)
где N – количество активов; wi – доля общего вложения, приходящаяся на i-й актив; Ei – ожидаемая доходность i-ого актива (%); Ep – ожидаемая доходность портфеля (%); σp – мера риска портфеля; σij – ковариация между доходностями i-ого и j-ого актива[6].
Одним из ограничений будет условие неотрицательности на доли ценных бумаг в портфеле, что обеспечивает работу с классическим портфелем состоящих из «длинных» позиций. Особенностью этого ограничения модели является предел доходности допустимого портфеля, т.к. доходность любого стандартного портфеля не превышает наибольшей доходности актива с максимальной доходностью входящего в портфель[7].
Выбор приемлемого, по характеристикам, портфеля ценных бумаг осуществляется с помощью кривых безразличия. Кривые безразличия графически отражают «терпимость» инвестора к риску. Предположения, сделанные относительно предпочтений, гарантируют, что инвесторы могут указать на предпочтение, отдаваемое одной из альтернатив или на отсутствие различий между ними.
На рисунке 1 представлена графическая, теоретическая интерпретация решения задачи, заключающаяся в поиске множества эффективных портфелей среди множества допустимых портфелей[8].
В модели Марковица, допустимыми являются только стандартные портфели (без коротких позиций).
В данной постановке задача Марковица решается с помощью методов динамического программирования [9, с.178]. Однако на практике при большом количестве активов и необходимости получения быстрых результатов, целесообразно использовать эвристические методы поиска.
В рамках данной научной работы, исследуется потенциальная возможность использования генетических алгоритмов для решения задачи Марковица, который необходимо адаптировать под каждую решаемую задачу, что находит отражение в научных трудах, указанных в источниках [10,11].
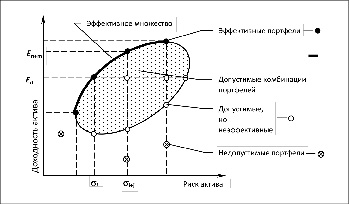
Рис. 1. Допустимое и эффективное множество решений Источник: разработан авторами на основе источника [8, с. 187]
Адаптация генетического алгоритма при решении отдельных классов оптимизационных задач в первую очередь касается формы представления решений и процедур кодирования и декодирования, которые должны быть разработаны и адаптированы в строгом соответствии с требованиями и характеристиками конкретной задачи. Не менее значимой является процедура кроссовера, которая должна быть модифицирована с учетом всех ограничений, накладываемых на решение задачи, и способствовать эффективному поиску оптимальных решений в пределах заданных условий. Таким образом, адаптация требует тщательного анализа и настройки для каждого индивидуального случая, что способствует достижению высокой эффективности при решении целевых задач.
Определим форму представления решений, которая определяет эффективность генетических операторов (скрещивание, мутация) и скорость сходимости алгоритма. Ниже приведен вариант с рекомендациями по применению. В первую очередь определим особь в форме вещественного представления.
Под особью xi будем понимать любое допустимое решение задачи (1) в форме вектора действительных чисел, следующего вида:
xi = {w1, w2,… wn}, (2)
где wi – доля i-ого актива.
Необходимо отметить, что особь должна соответствовать ограничениям задачи (формула 1) [12,13].
Под популяцией, в контексте генетического алгоритма, будем подразумевать массив допустимых решений P[K], где K – количество особей в популяции.
Первичная популяция, представленная выражением (3):
P0[K] = {x1, x2,…x k}, (3)
формируется случайным образом с использованием генератора псевдослучайных чисел, работающего по равномерному закону распределения. Это обеспечивает начальное разнообразие решений, необходимое для эффективного исследования пространства поиска.
В качестве функции приспособленности в рамках рассматриваемой задачи выступает функция оценки доходности портфеля, представленная формулой (4), определяющая направление и эффективность поиска оптимального решения на каждой итерации вычислительного процесса:
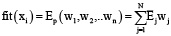 (4)
(4)
Популяция особей, как некоторое множество допустимых решений, будет характеризоваться значимыми для нас величинами:
1) Максимальное значение функции fitmax (Pi[K])
2) Среднее значение функции fitav(Pi[K])
Допустимые решения, которые использует генетический алгоритм при проведении операций, представлены в двоичной форме, поэтому необходимо определиться с понятием функции кодирования и декодирования представленных выражениями (5) и (6). Если xi – особь(допустимое решение), а hi – хромосома(двоичное представление допустимого решения) то функцией декодирования будет являться функция такая, что:
x1 = dec(hi) (5)
а функцией кодирования будет являться функция такая, что:
h1 = cod(xi) (6)
Программный принцип этих функций представлен на рисунке 2.
Стоит отметить, что для поставленных целей достаточно использовать целочисленные значения долей wi. Если требуется более высокая точность необходимо увеличивать разрядность двоичной хромосомы[13].
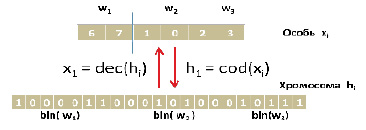
Рис. 2. принципы кодирования и декодирования для особей из 3х активов Источник: разработан авторами
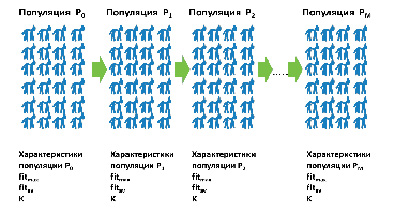
а) Схематичное представление эволюционного процесса, с изменением характеристик популяций
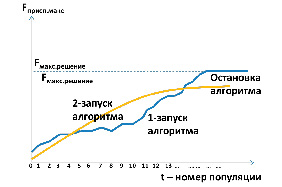
б) теоретический вид динамики функции приспособленности
Рис. 3. Моделирование эволюционного процесса Источник: разработан авторами
В результате применения генетических операторов, следует последовательная смена поколений[14], что моделирует процесс эволюции, в конце которой получаем популяцию с квази-оптимальными значениями функции приспособленности. Данный процесс отражен на рисунке 3.
Переход между поколениями популяций в генетическом алгоритме – ключевой цикл эволюционного процесса, обеспечивающий улучшение решений. Переход из поколения Pn в поколение Pn+1 осуществляется через последовательное применение генетических операторов: селекции, кроссовера (скрещивания) и мутации[15,16,17]. Эти операторы имитируют биологические механизмы естественного отбора, рекомбинации генов и случайных изменений.
Для осуществления селекции должен существовать механизм, с помощью которого формируется некоторое множество P[Q] представляющее собой некоторое подмножество особей из популяции Pj[N] которые имеют возможность быть родителями и передавать свою генетическую информацию, процесс схематично отражен на рисунке 4. Такое подмножество называется родительским пулом.
Основные алгоритмы формирования родительского пула, следующие:
1) элитарный способ;
2) селекция турнирным методом;
3) метод «рулетки».
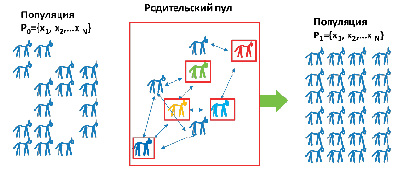
Рис.4. Формирование родительского пула Источник: разработан авторами
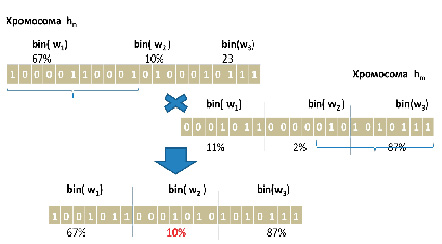
а) устройство оператора кроссовера с одной точкой
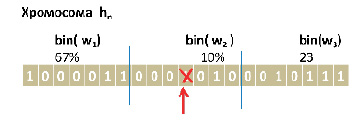
б) устройство оператора мутации с одной точкой
Рис. 5. Устройство операторов кроссовера и мутации в генетическом алгоритме Источник: разработан авторами
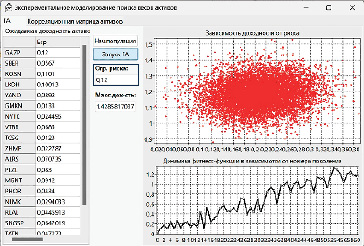
а) экранная форма поиска квази-оптимального значения функции приспособленности
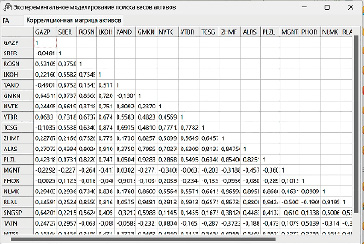
б) корреляционная матрица 20 ценных бумаг Мосбиржи
Рис. 6. Экспериментальные результаты работы алгоритма оптимизации Источник: разработан авторами
После формирования родительского пула P[Q] проводим операции кроссовера и мутации, принцип работы которых, представлен на рисунке 5.
Как видим из рисунка 5а в результате кроссовера, получается хромосома с недопустимыми параметрами(в данном случае сумма весов превышает 100%). Полученная хромосома требует проведения нормализации и замены данной хромосомы на эквивалентную с сохранением пропорции долей, указанных в генах.
Экспериментальное исследование эффективности генетического алгоритма для решения задачи Марковица проводилась с использованием приложения разработанного в среде разработки Lazarus IDE, для выборки из 20 акций индекса Мосбиржи (идентификаторы активов: GAZP, SBER, ROSN, LKOH, YAND, GMKN, NVTK, VTBR, TCSG, ZHMF, ALRS, PLZL, MGNT, PHOR, NLMK, RLAL, SNGSP, TATN, MTSS, PIKK). Оценка уровня доходности, риска и корреляции проводилась на исторических данных о дневных котировках за 3–5 лет.
Параметры генетического алгоритма, использующиеся для проведения эксперимента:
– размер популяции: 100–500 особей;
– вероятность мутации: 1–5%;
– критерий остановки: стагнация функции приспособленности за 15 поколений.
Экспериментальные результаты работы алгоритма оптимизации представлены на рисунке 6а. В тестовой версии программы, корреляция предустановлена в виде массива констант, отраженного на рисунке 6б. Ограничение по уровню риска задается полем «Огр.риска», результат поиска максимальной доходности приведен в поле «Макс.дох-ть», на рисунке 6а.
Нахождение с помощью генетического алгоритма квази-оптимальных решений задачи максимизации доходности портфеля, при ограничении риска происходит, при достаточно большой ёмкости портфеля состоящего из двадцати активов, за приемлемое время, примерно 60-70 это итераций.
Заключение
Проведённое исследование позволяет заключить, что генетические алгоритмы обладают рядом преимущества и недостатков, однако эмпирическое исследование показало их эффективность при решении задач оптимизации поставленных Марковицем.
Реализованный генетический алгоритм устойчив к локальным оптимумам и благодаря механизму мутации и селекции избегает «застревания» в локальных минимумах, что критично для невыпуклых функций в модели Марковица.
При необходимости адаптации к многокритериальности (например ликвидности активов), могут использоваться модифицированные генетические алгоритмы SPEA, а также применяться методы ниширования (niching) и разделения приспособленности (fitness sharing), что позволит поддерживать разнообразие решений. Это особенно важно при учёте дополнительных параметров.



