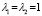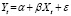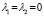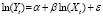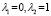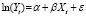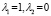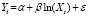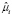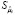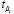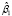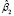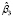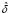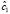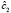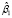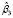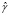Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Введение

Объемы кредитования физических и юридических лиц неуклонно растут, о чем свидетельствуют статистические показатели банковского сектора Российской Федерации [1] (рис. 1–3). За 2023 г. объем кредитования физических лиц вырос на 23 %, что существенно выше роста на 9,5 % в 2022 г. Эксперты объясняют такой взлет объемов кредитования отложенным спросом и ростом объемов субсидирования кредитных ставок [2].

Объем кредитования юридических лиц в 2023 г. увеличился на 25 %, в 2022 г. – на 11 %. Величина корпоративного кредитного портфеля по итогам 2023 г. составила приблизительно 74 млн руб., поднявшись за этот период на 14723,6 млн руб. [1] (рис. 2). Рост объема кредитования юридических лиц во многом обеспечил сегмент малого и среднего бизнеса (МСБ), так как были образованы новые логистические связи с дружественными странами, а после ухода из России крупных иностранных компаний МСБ получил доступ к новым рыночным нишам [3].

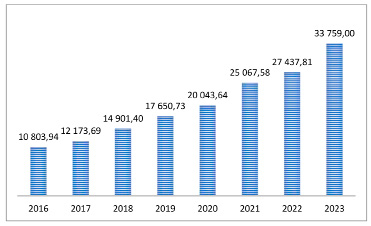
Рис. 1. Объемы кредитования физических лиц, млрд руб

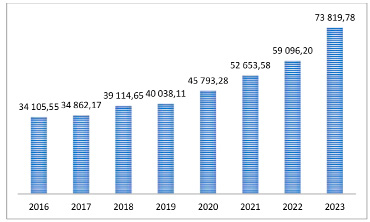
Рис. 2. Объемы кредитования юридических лиц

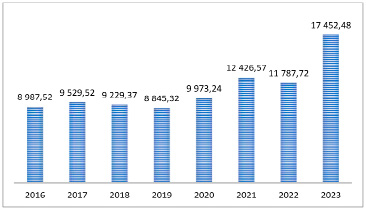
Рис. 3. Объемы межбанковского кредитования

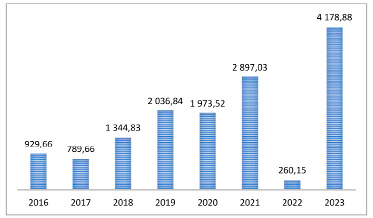
Рис. 4. Прибыль банков до налогообложения

В период с 2019 по 2021 г., а также в 2023 г. рост также наблюдался и на рынке межбанковских кредитов (МБК) [1] (рис. 3). Рекордный рост был зафиксирован Центральным банком по итогам 2023 г. Прирост объема МБК составил 48 % по сравнению с 2022 г. Межбанковское кредитование регулирует текущую ликвидность и поддерживает платежеспособность всей банковской системы. Межбанковский кредит представляет собой инструмент денежного рынка, на котором происходит кредитование одного банка другим под небольшой процент (по межбанковской ставке) в форме кредитной линии на срок чаще всего от одной ночи до недели [4].

Кредитная деятельность коммерческого банка является одним из основных источников формирования его прибыли. Динамика прибыли до налогообложения с 2016 по 2023 г. представлена на рис. 4 [1]. По итогам кризисного 2022 г. российские банки зафиксировали прибыль (до налогообложения) с рекордно низким показателем 260,15 млрд руб. По сравнению с результатом 2021 г. прибыль кредитных организаций упала в 11 раз. Однако в 2023 г. коммерческие банки смогли увеличить прибыль в 16 раз по сравнению с 2022 г.

Основным источником прибыли российских банков являются процентные доходы [5]. К процентным доходам относятся доходы по кредитам; от использования средств на расчетных, текущих и прочих счетах до востребования; от использования средств по срочным вкладам; от факторинговых и форфейтинговых операций. Наибольшую долю процентных доходов коммерческих банков занимают проценты по выданным кредитам [6].

Целью исследования является количественная оценка вклада в формирование прибыли банков объемов выданных кредитов физическим, юридическим лицам и межбанковских кредитов.

Материалы и методы исследования

Для реализации поставленной цели авторы используют методы эконометрики для работы с панельными данными. Выборочные данные содержат панели 29 российских банков (табл. 1) с 2012 по 2021 г., в том числе панели 6 системно значимых банков (Сбербанк, Альфа-Банк, Московский Кредитный банк, Райффайзенбанк, ЮниКредит Банк, Тинькофф банк). Источником данных послужила информационная система «Спарк».

В первом разделе статьи авторы проводят обзор ряда эконометрических исследований банковского сектора России. Во втором разделе проводится тестирование и выбор спецификации модели. Для выбора спецификации используются процедуры Бокса – Кокса и Зарембки. Третий раздел посвящен оценке и анализу моделей на панельных данных: объединенной, с фиксированными эффектами и со случайными эффектами. В четвертом разделе оценивается двунаправленная модель с фиксированными эффектами для учета общих для всех банков структурных изменений, связанных с введением санкций. Наконец, в пятом разделе в модель с фиксированными эффектами вводятся переменные, постоянные во времени для выделения в модели системно значимых банков.

Эконометрическим исследованиям финансово-экономических показателей банковского сектора посвящено множество работ. В работе [7] эконометрический инструментарий используется для моделирования различных финансово-экономических показателей деятельности ПАО Сбербанк. Исследование [8] также посвящено моделированию показателей деятельности ПАО Сбербанк. Авторами построены две группы моделей: модели влияния финансовых показателей на прибыль банка; модели влияния социально-экономических показателей страны на прибыль банка. Эконометрическому исследованию влияния макроэкономических показателей российской экономики на активы российских банков посвящено исследование [9]. В качестве экзогенных переменных авторы рассматривают номинальный ВВП, темп роста ВВП в рублях и долларах, прямой обменный курс доллара, индекс потребительских цен, ключевую ставку ЦБ.

Таблица 1

Исследуемые российские банки

В работе [10] представлена разработанная автором эконометрическая модель банковского кредитования юридических лиц в Республике Беларусь. Спецификация модели в качестве эндогенных переменных включает долгосрочные и краткосрочные кредиты, выданные юридическим лицам в национальной валюте, и краткосрочные кредиты, выданные юридическим лицам в иностранной валюте. Экзогенными переменными являются денежная масса (агрегат M3), ставка рефинансирования Национального банка, инвестиции в основной капитал, индекс цен производителей промышленной продукции и др.

В работе [11] автором построена модель векторной авторегрессии для прогнозирования состояния кредитного рынка. Эндогенными переменными модели являются объем выданных кредитов, объем привлеченных депозитов и ряд других показателей.

В работе [12] предложены модели временных рядов, объясняющие уровни квартальных объемов кредитования физических лиц Самарского региона, объемы погашения и уровень ссудной задолженности с учетом внешних шоков.

Работа [13] посвящена исследованию связи депозитов и кредитов в российских банках. Авторы используют методику, основанную на идее коинтеграционного анализа случайных процессов с применением векторной модели коррекции ошибок, оцениваемой по панельным данным. Исследование авторов выявило невыполнение классического принципа независимости депозитов и кредитов в российской банковской системе. Авторы показали, что формирование кредитного рынка происходило с 2015 по 2020 г. в соответствии с тактикой стабильного фондирования. Выявлена независимость депозитов от кредитов, обуславливающая тот факт, что рост денежной массы в России происходит не за счет расширения инвестиционных возможностей банков, а путем эмиссии, что указывает на несовершенство российской банковской системы для обеспечения экономического роста, превалирование роли ЦБ и относительную несамостоятельность банков.

Эконометрическое исследование [14] посвящено оценке риска невыплат по потребительским кредитам. Авторы используют двумерную пробит-модель, в которой зависимые переменные были определены как «Наличие потребительского кредита на момент опроса», принимающие значение 1 в случае наличия кредита и 0 в случае его отсутствия, и переменная, сформированная по ответам на вопрос «В течение последних 12 месяцев были ли случаи, когда Ваше домохозяйство оказывалось не в состоянии внести очередной платеж, такой как плата за арендуемое жилье; оплата счетов за квартплату, коммунальные услуги…», принимающая значение 1 в случае наличия долга и 0 в случае его отсутствия. В число объясняющих переменных модели были включены: демографический тип домохозяйства, уровень образования респондента, число занятых в домохозяйстве и др.

В статье [15] построена экспоненциальная модель, объясняющая величину выдаваемых ипотечных кредитов процентной ставкой по кредиту и месяцем года выдачи кредита. В модели авторов значащими оказались фиктивные переменные, соответствующие первым трем месяцам календарного года. Коэффициенты при этих переменных указывают, на то, что спрос на ипотечные кредиты в первые месяцы года существенно ниже.

Результаты исследования и их обсуждение

Для выбора формы взаимосвязи между переменными модели, к настоящему времени разработано множество формальных тестов (Рамсея RESET), Песарана (PE-тест) и J-тест, основанных на построении моделей искусственного вложения. Из-за многообразия и сложности экономических процессов при выборе спецификации модели обычно выполняют ее тестирование на неспецифицированную нелинейность. Большинство функциональных форм эконометрических моделей описывается при помощи преобразования Бокса – Кокса – однопараметрического семейства преобразований вида

,

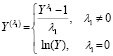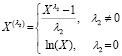. (1)

Частные случаи преобразования (1) обобщенной регрессионной модели Бокса – Кокса

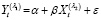(2)

приведены в табл. 2.

Таблица 2

Частные случаи обобщенной модели Бокса – Кокса

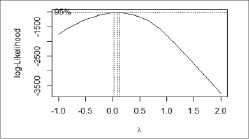
Рис. 5. Выбор оптимального значения параметра λ модели Бокса – Кокса

Параметры λ модели (2), в эконометрических пакетах, оцениваются методом максимального правдоподобия по выборочным данным при помощи «решетчатой» процедуры, позволяющей найти максимальное значение логарифмической функции правдоподобия для сетки , .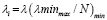

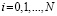Для подбора функциональной формы модели зависимости прибыли банка (Y) от выданных кредитов физическим (X1), юридическим (X2) лицам и межбанковских кредитов (X3) по выборке, включающей объединенные данные по 29 российским банкам за период с 2012 по 2021г., была использована функция boxcox() пакета MASS программной среды R. График значений логарифмической функции правдоподобия для параметра λ (в диапазоне от -1 до 2) приводится на рис. 5.

Значение параметра λ, полученное для уровня значимости 0,05, близко к нулю, то есть на основании теста Бокса – Кокса можно предположить логарифмически-линейную зависимость между переменными модели (табл. 2).

Для сравнения линейной,

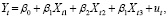(3)

и логарифмически-линейной,

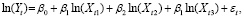(4)

моделей – моделей с разными эндогенными переменными, для обеспечения их сопоставимости, Полом Зарембкой была предложена упрощенная процедура теста Бокса – Кокса, в которой значения эндогенной переменной моделей вычисляются по формуле

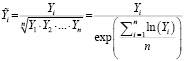. (5)

Результаты оценивания моделей (3) и (4) с эндогенной переменной (5) по выборочным данным приведены в стандартной форме:

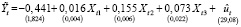, (6)

ESS1 = 241845,9, R2 = 0,967, F = 2798.

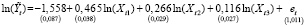, (7)

ESS2 = 292,38, R2 = 0,847, F = 527.

Статистическая значимость различия в качестве сравниваемых моделей (6) и (7) определяется при помощи статистики, имеющей χ2 – распределение:

,

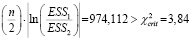то есть при уровне значимости α = 0,05 результаты линейной и логарифмически-линейной моделей различаются статистически значимо. Логарифмически-линейная модель

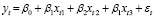, (8)

где yt = ln(Yt), xt1 = ln(Xt1), xt2 = ln(Xt2), xt3 = ln(Xt3), лучше согласуется с выборочными данными и поэтому выбрана для построения моделей для панельных данных.

Эконометрический инструментарий для панельных данных включает три основные регрессионные модели: объединенную модель (pooled model), модель с фиксированными эффектами (fixed effects model, FE), модель со случайными эффектами (random effects model, RE). Для оценки параметров статических вариантов объединенной модели и модели с фиксированными эффектами (при условии выполнения предпосылок теоремы Гаусса – Маркова) используется МНК (метод наименьших квадратов), для модели со случайными эффектами – ОМНК (обобщенный МНК). При большом количестве панелей, для состоятельного оценивания параметров моделей с фиксированными эффектами, применяется процедура раздельного оценивания параметров влияния и местоположения. При практической реализации ОМНК используется доступный ОМНК (ДОМНК), который сводится к МНК для преобразованных переменных.

Оценка и статистический анализ моделей для панельных данных осуществлялись в программной среде R при помощи функции plm одноименного пакета. Для извлечения индивидуальных эффектов моделей с фиксированными эффектами использовалась функция summary(fixef()).

Оценка моделей для панельных данных была выполнена по сбалансированным панелям: n = 29 – число панелей, T = 10 – число наблюдений в панели, N = 290 – число выборки панельных данных. Оценки параметров при регрессорах объединенной модели положительные и статистически значимы при уровне значимости α = 5% (значения t-статистик оценок параметров приводятся в скобках под оценками параметров):

.

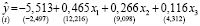Судя по коэффициенту детерминации и значению F-статистики, объединенная модель высокого качества и статистически значима:

R2 = 0,847, 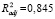, F = 527,01,

сумма квадратов остатков модели:

ESSpooled = 292,38.

Оценка исходной степенной модели получается обратным преобразованием:

.

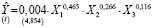Максимальной эластичностью является эластичность прибыли банка по кредитам физических лиц (при увеличении на 1% кредитов, выданных физическим лицам (X1), прибыль банка возрастает на 0,47 %).

Для оценки параметров модели с фиксированными эффектами использовалась процедура раздельного оценивания параметров местоположения и влияния. Параметры влияния оценены в рамках внутригрупповой регрессии (модель m1)

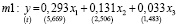, (9)

R2 = 0,942, F = 149,88,

ESS = 110,54, ESSFE = 110,54.

Таблица 3

Параметры местоположения модели FE (m1)

Значения t-статистик оценок параметров показывают статистическую значимость влияния на прибыль банка кредитов физическим и юридическим лицам (при уровне значимости α = 5%). В модели с фиксированными эффектами коэффициент детерминации вычислялся как квадрат индекса корреляции – корреляции между вектором значений эндогенных переменных и вектором их оценок, полученных при помощи модели FE. Коэффициент детерминации в модели с фиксированными эффектами выше, чем в объединенной модели, а сумма квадратов остатков – ниже. Оценки индивидуальных эффектов 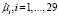и их стандартные ошибки для модели (9) приводятся в табл. 3.

Во втором столбце табл. 3 приведены оценки параметров местоположения, в третьем – их стандартные ошибки, в четвертом – t-статистики, в пятом – значения p-value, по которым видно, что индивидуальные фиксированные эффекты статистически значимы (при α = 5%) практически для всех банков за исключением Синко-Банка и Трансстройбанка. Индивидуальные особенности каждого банка играют важную роль при оценке его прибыли, так как отражают влияние других, не учтенных в рамках данного исследования факторов.

В оцененной модели со случайными эффектами,

,

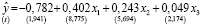R2 = 0,844, F = 272,302, ESSFE = 133,06.

t-статистики оценок параметров при регрессорах статистически значимы.

Выбор типа модели для панельных данных базируется на трех специальных статистических тестах и стандартной технике проверки статистических гипотез, которые реализованы, в частности, в пакете plm программной среды R. Для сравнения объединенной модели (модели без эффектов) и модели с фиксированными эффектами был использован F-тест (функция pFtest()), который показал значимость специфических эффектов (F = 15.157, df1 = 28, df2 = 258, p-value < 2.2e-16). Случайные специфические эффекты также оказались значимыми при тестировании объединенной модели против модели со случайными эффектами при помощи теста множителей Лагранжа (функция plmtest() ): chisq = 326.07, df = 1, p-value < 2.2e-16. Сравнение фиксированных и случайных эффектов (тест Хаусмана (функция phtest()) свидетельствует в пользу фиксированных (chisq = 24.854, df = 3, p-value = 1.657e-05).

Таким образом, результатом формального тестирования типа модели для панельных данных является отклонение нулевых гипотез тестов множителей Лагранжа, Хаусмана и F-теста в пользу модели с фиксированными эффектами. Результат тестирования не является неожиданным, модели с фиксированными эффектами, как правило, адекватно описывают взаимосвязь между экономическими переменными для объектов, представляющих собой крупные регионы, большие предприятия, крупные банки (в частности, системно значимые).

Санкции, введенные против Российской Федерации, включают в себя в том числе и масштабные ограничения финансовой системы, приводящие к структурным изменениям в банковской сфере. Для моделирования общих для всех экономических объектов структурных изменений, зависящих от времени, в модель c фиксированными эффектами

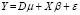, (10)

где 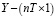– вектор значений эндогенной переменной, 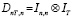– матрица индивидуальных фиктивных переменных, учитывающая гетерогенность панельных данных, 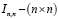– единичная матрица, 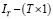– единичный столбец, 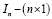– единичный столбец, 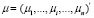– вектор параметров местоположения, характеризующий ненаблюдаемые специфические особенности банков, 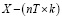– матрица регрессоров, 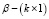– вектор параметров влияния, 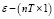– вектор возмущений, вводится дополнительная переменная γ, формализующая влияние особенностей различных лет исследуемого периода на эндогенную переменную

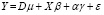, (11)

, ,

,

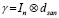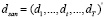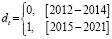dt – бинарная переменная, учитывающая влияние санкций на эндогенную переменную модели в момент времени t и принимающая значение 0 до их введения, 1 – после, α – параметр при фиктивной переменной. Показатели качества и статистической значимости двунаправленной модели (11) с фиктивными переменными, учитывающими санкционный период (ms1), выше, чем в модели (9):

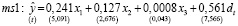, (12)

R2 = 0,952, F = 185,31, ESSsan = 90,409.

Значения t-статистик оценок параметров показывают статистическую значимость влияния на прибыль банка кредитов, выданных физическим и юридическим лицам (при уровне значимости α = 5 %). Влияние межбанковских кредитов статистически незначимо. Формальный тест отвергает гипотезу о равенстве нулю коэффициента при бинарной переменной времени в (12), следовательно, введение санкций существенно повлияло на прибыль банков. Оценки индивидуальных фиксированных эффектов и их стандартные ошибки приводятся в табл. 4.

Статистическая значимость оценок параметров модели с фиксированными эффектами с введением фиктивной переменной, учитывающей санкционный период, существенно повысилась.

Таблица 4

Параметры местоположения модели (10) (ms1)

Модель с фиксированными эффектами имеет существенный недостаток. Она не позволяет идентифицировать параметры при переменных, которые не меняются со временем. Например, чтобы учесть влияние некоторых качественных признаков (направление деятельности, принадлежность к системно значимым банками и т.д.), в спецификацию модели (10) вводится матрица фиктивных переменных Z с постоянными во времени значениями:

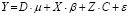. (13)

На этапе внутригруппового преобразования переменных модели (5.1):

, ,

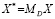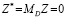где 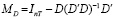– матрица внутригруппового преобразования, 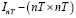– единичная матрица, при оценке параметров FE-модели методом наименьших квадратов

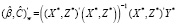, (14 )

где (X*,Z*) – блочная матрица регрессоров модели, 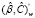– блочный вектор столбец параметров, появляется проблема полной мультиколлинеарности. Таким образом, вектор параметров C в модели (13) не идентифицируем.

Для решения проблемы включения в модель с фиксированными эффектами переменных, не изменяющихся во времени, в 2007 г. Трёгером была предложена трехшаговая процедура. На первом шаге, по выборочным панельным данным, методом раздельного оценивания вычисляются оценки параметров влияния и местоположения модели с фиксированными эффектами (10). На втором шаге выполняется декомпозиция вектора фиксированных эффектов: оценивается регрессия, в которой вектором эндогенной переменной является n-мерный вектор оценок параметров местоположения 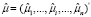(оцененных индивидуальных фиксированных эффектов для каждого банка, второй столбец табл. 4). Регрессия строится на константу и n-мерный вектор столбец фиктивной переменной Z, не изменяющейся во времени (zi = 1, i = 1,…,n, если банк относится к системно значимым, zi = 0 в противном случае, столбец 6 табл. 4), отражающей влияние качественного признака

m2: 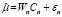, (15)

где Wn = (in, Zn) – матрица регрессоров, включающая единичный n-мерный столбец in, Cn – вектор параметров модели (15), εn – вектор возмущений. Оцененная модель второго шага (15) для фиксированных эффектов модели (10), среднего качества, статистически значима и имеет значимые оценки параметров:

,

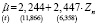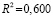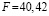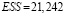, , . (16)

Далее, по оцененной модели (16) вычисляется вектор остатков ez, который (как и вектор фиктивных переменных Zn) при помощи матрицы фиктивных переменных D распространяется на все панели:

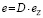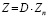, . (17)

На третьем шаге оценивается модель, включающая помимо регрессоров модели (10) регрессоры (17), постоянный во времени фиктивный регрессор Z и вектор остатков e вспомогательной модели (16):

m3: 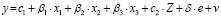, (18)

где c1, c2, β1, β2, β3, δ – параметры модели, v – случайное возмущение.

Результат оценивания модели (18):

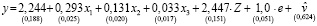. (19)

Модель m3, полученная на третьем шаге, объединяет результаты первого (модель m1) и второго (модель m2) шагов. Оценки параметров модели m2 – c1, c2 в (16) совпадают с оценками параметров модели (17), оценки параметров β1, β2, β3 в (9) совпадают с оценками параметров модели (19), параметр δ = 1. Однако точность оценок параметров в модели (19) несколько выше, чем у соответствующих оценок параметров моделей первого и второго шагов. Остатки модели с фиксированными эффектами (m1) совпадают с остатками модели третьего шага (m3), поэтому их суммы квадратов тоже совпадают, а разность в числе степеней свободы объясняет неравенство для стандартных ошибок моделей:

.

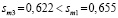Асимптотическая ковариационная матрица для вектора оценок параметров модели Трёгера (m3) меньше, чем для вектора оценок параметров модели с фиксированными эффектами (m1). В табл. 5 приводятся оценки параметров и их стандартные ошибки (в скобках) для моделей (9), (16), (19).

Таблица 5

Оценки параметров моделей процедуры Трёгера без учета санкций

Таблица 6

Оценки параметров моделей процедуры Трёгера с учетом санкций

Как следует из табл. 5, оценки параметров влияния модели (9), не учитывающей санкционное давление на РФ со стороны западных стран (столбец 2 табл. 5), совпадают с оценками параметров модели, оцененной методом Трёгера (столбец 4 табл. 5), однако точность последних значительно выше. В табл. 6 приводятся оценки параметров и их стандартные ошибки (в скобках) для моделей с фиксированными эффектами, учитывающими санкционное влияние.

Заключение

В результате формального тестирования моделей для панельных данных, описывающих зависимость прибыли банков от объемов кредитов, выданных физическим, юридическим лицам, и межбанковских кредитов, выбрана модель с фиксированными эффектами. Временной интервал, охватывающий панельные данные, включает период до и после санкционного давления. Как показали результаты исследования, бинарная фиктивная переменная, включенная в расширенную модель с фиксированными эффектами для описания влияния структурных изменений, зависящих от времени, статистически значима и ее включение позволило повысить качество и статистическую значимость оцениваемой модели. Введение фиктивных переменных, не зависящих от времени, в модель с фиксированными эффектами приводит к проблеме неидентифицируемости параметров при этих переменных. Одним из способов решения этой проблемы является трехшаговая процедура Трёгера. Применение этой процедуры к расширенной модели с фиксированными эффектами для учета индивидуальных особенностей банков, включенных в список системно значимых, позволило решить проблему неидентифицируемости параметров при фиктивных переменных, не изменяющихся во времени, и значительно повысить точность результатов оценивания. Согласно модели (19), точность оценок которой оказалась наиболее высокой среди рассмотренных в статье моделей, прирост объема кредитования физических лиц в России на 1 % способствует увеличению прибыли российских банков на 0,29 %; прирост объема кредитования юридических лиц на 1 % приводит к приросту прибыли на 0,13 %; прирост межбанковских кредитов на 1 % сопряжен с увеличением прибыли на 0,03 %.