В основу известных теоретических и прикладных методов проектирования систем подвижной радиосвязи в настоящее время положен подход классической теории массового обслуживания, ориентирующийся на фиксированный уровень общей нагрузки, который понимается, как заданный внешними условиями. Для существующих систем связи подвижных абонентов, включая сотовые сети вплоть до 2-го поколения, он вполне оправдан, хотя в определенных ситуациях не позволяет обеспечить нужную точность. Справедливость использования методов классической теории массового обслуживания основывается на том, что зонное покрытие в системах до 2-го поколения организовано так, что отдельные БС обслуживают большое число абонентов с низкой удельной средней нагрузкой (от 0.001 до 0.03 Эрл./абонент). Из-за измельчения структуры покрытия и увеличения удельной нагрузки для систем 3G, даже при наличии условий стационарности и однородности, оказывается неверным закон Эрланга, повсеместно утвердившийся в качестве инструмента решения задач разработки и анализа систем связи. Он трансформируется в закон Энгеста-О’Делла, для которого уже не существует однозначной связи между средней нагрузкой и вероятностью блокировок. Поэтому становится важно, не только понять, как решать задачи борьбы с перегрузками в новых условиях, но и определить границы применимости традиционных методов, установить каким именно образом уменьшение размеров сот, повышение мобильности и, может быть, некоторых других параметров влияет на эти границы.
Изменение профиля современных систем связи, в котором основной режим отводится обмену цифровыми данными, приводит к тому, что удельное значение нагрузки на абонента существенно увеличивается. При этом информационные потоки приобретают прямую связь с потоками мобильности. Локальные концентрации абонентов, возникающие по причине автомобильных пробок, проведения массовых мероприятий, возникновения внешних синхронизирующих условий непосредственно порождают локальные перегрузки в информационных потоках. В таких условиях особое значение приобретают вопросы создания адекватных описательных моделей и методов контроля мобильности на уровне отдельных сот/зон. В качестве технической основы для решения поставленной задачи может выступать служба контроля мобильности (слой ММ), которая применяется в существующих системах для решения задач ограниченного поиска абонентов при вызовах и поддержки непрерывной связи. Таким образом для эффективного использования пропускной способности системы по трафику необходимо иметь более общие модели системы, как системы массового обслуживания, и, на их основе, синтезировать алгоритмы динамического управления ресурсом системы. В этой постановке интенсивность Пуассоновского потока ![]() изменяется во времени как стохастический диффузионный процесс, удовлетворяющий уравнению движения в форме Ито:
изменяется во времени как стохастический диффузионный процесс, удовлетворяющий уравнению движения в форме Ито:
![]() , (1)
, (1)
где ![]() - порождающий процесс для уравнения движения в виде белого гауссовского шума (БГШ) с единичной двусторонней спектральной плотностью мощности (
- порождающий процесс для уравнения движения в виде белого гауссовского шума (БГШ) с единичной двусторонней спектральной плотностью мощности (![]() =1),
=1), ![]() и
и ![]() - известные постоянные параметры.
- известные постоянные параметры.
Известно, что уравнение (1) описывает Марковский диффузионный процесс с коэффициентами сноса и диффузии:
![]() ;
; ![]() .
.
Уравнение Фокера-Планка-Колмогорова (ФПК), описывающее плотность вероятности ![]() , при этом будет таким:
, при этом будет таким:
![]()
![]() . (2)
. (2)
В установившемся состоянии плотность вероятности, согласно (2), должна удовлетворять уравнению:
![]() .
.
Последнее уравнение можно проинтегрировать, с учетом того, что, согласно физическому смыслу задачи, ![]() . В результате получим:
. В результате получим:
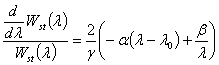 . (3)
. (3)
Дифференциальное уравнение (3) имеет решение:
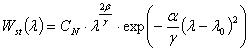 , (4)
, (4)
где ![]() - коэффициент нормировки, точное представление которого не имеет принципиального значения.
- коэффициент нормировки, точное представление которого не имеет принципиального значения.
Из (4) видно, что модель (1) при различном выборе коэффициентов может приводить к стационарным распределениям параметра интенсивности ![]() , подчиняющимся многомерным законам Релея, Гаусса или законам близким к распределению Райса.
, подчиняющимся многомерным законам Релея, Гаусса или законам близким к распределению Райса.
Наблюдению доступна реализация Пуассоновского потока с моментами возникновения событий
![]() . (5)
. (5)
Предполагаем, что известны параметры уравнения движения (1) и доступны наблюдения моментов Пуассоновского потока (5), а также начальное распределение интенсивности, которое достаточно хорошо аппроксимирует нормальный закон:
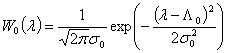 , (6)
, (6)
где ![]() и
и ![]() - априорные среднее и дисперсия интенсивности
- априорные среднее и дисперсия интенсивности ![]() , причем
, причем ![]() , что позволяет не принимать во внимание возможность
, что позволяет не принимать во внимание возможность ![]() в априорном распределении (6).
в априорном распределении (6).
В таких условиях требуется решить задачу фильтрации стохастического процесса ![]() . Для решения поставленной задачи воспользуемся методикой инвариантного погружения. При этом придется выполнить ее обобщение. Действительно, при выводе уравнений фильтрации с помощью техники инвариантного погружения (приближенная методика) используется компонента, связанная с наблюдениями, в виде предельного отношения:
. Для решения поставленной задачи воспользуемся методикой инвариантного погружения. При этом придется выполнить ее обобщение. Действительно, при выводе уравнений фильтрации с помощью техники инвариантного погружения (приближенная методика) используется компонента, связанная с наблюдениями, в виде предельного отношения:
![]() , (7)
, (7)
где ![]() - плотность вероятности наблюдения на интервале
- плотность вероятности наблюдения на интервале ![]() процесса
процесса ![]() , при условии того, что фильтруемый сигнал на том же интервале имеет вид
, при условии того, что фильтруемый сигнал на том же интервале имеет вид ![]() . В традиционной постановке предполагается, что в канале наблюдения присутствует аддитивная смесь полезного сигнала
. В традиционной постановке предполагается, что в канале наблюдения присутствует аддитивная смесь полезного сигнала ![]() и белого гауссовского шума
и белого гауссовского шума ![]() с двусторонней спектральной плотность мощности
с двусторонней спектральной плотность мощности ![]() . При этом (7) приводит к
. При этом (7) приводит к
![]() ,
,
а в уравнениях фильтрации появляется составляющая, пропорциональная
![]() (8)
(8)
и пропорциональная
![]() (9)
(9)
- в уравнениях для дисперсии ошибки фильтрации.
В нашем случае ![]() будет иметь другой вид, т.к.
будет иметь другой вид, т.к.
![]()
Подставляя в(7) последнее соотношение, находим
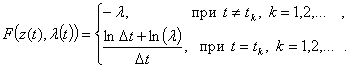
Соответственно, в уравнениях фильтрации следует вместо (8) и (9) использовать
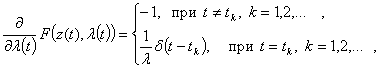 (10)
(10)
и
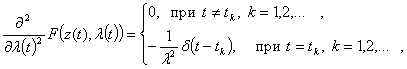 (11)
(11)
где ![]() - дельта-функция Дирака с особенностью в точке (моменте) t = tk.
- дельта-функция Дирака с особенностью в точке (моменте) t = tk.
Выполняя указанную подстановку, приходим к искомым уравнениям фильтрации интенсивности Пуассоновского потока:
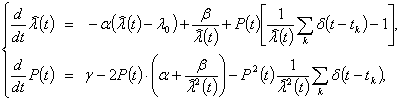 (12)
(12)
Решение системы (12) следует производить с начальными условиями
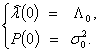 (13)
(13)
Совокупность уравнений (12) и (13) определяет решение поставленной задачи фильтрации интенсивности пуассоновского потока (1), (5). Соответствующий алгоритм может быть реализован с помощью доступных технических средств.



