Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Актуальность состоит в том, что в современных исследованиях все чаще используются системы искусственного интеллекта для поиска закономерностей при анализе развития и устойчивости российских коммерческих банков, чтобы обеспечить поддержку принятия оптимальных решений. Цель исследования состоит в исследовании теоретических основ развития отечественных банков, выявлении закономерностей их развития и устойчивости в современных условиях на основе использования различных моделей с последующим сравнением полученных результатов. Научная новизна в том, что выдвинута и доказана гипотеза, что, применяя современные методы исследования, в частности модель ML – модель «Случайный лес», могут быть выявлены определенные закономерности и получен прогноз требуемого параметра. Среди ключевых факторов, которые обуславливают в последнее десятилетие радикальные структурные сдвиги в мировой экономике, следует отметить повышение экономической роли инноваций. Прежде всего это связано с фундаментальными техническими и технологическими сдвигами, которые легли в основу крупномасштабных социально-экономических перемен. В связи с этим меняется и набор основных факторов экономического роста. По мнению А. Штайбера и С. Аланге, большинство попыток сохранения устойчивого развития относятся к организационным инновациям. Фирмам необходимо постоянно меняться из-за внедрения технологических новшеств, им следует эффективнее применять на практике инновации касательно организации бизнес-процессов, чтобы поддерживать собственную конкурентоспособность [1].

Материалы и методы исследования

В ходе проведения настоящего исследования были использованы такие методы, как метод k-средних, иерархическая кластеризация и модель глубокого обучения DL-модель «Случайный лес», причем расчеты были проведены в облачном сервисе Google Collab с использованием скриптов на языке Python [2]. Для формирования ML-модели «Random forest» были импортированы и использованы такие библиотеки, как DecisionTreeRegressor, matplotlib, numpy, sklearn.tree, xlrd, pandas.

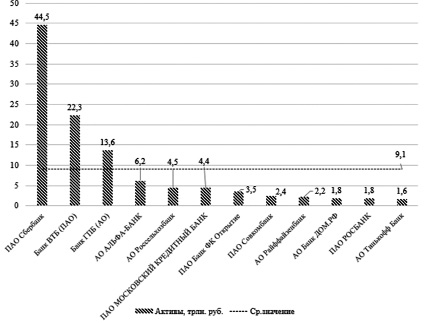
Рис. 1. Гистограмма активов российских банков, вошедших в Топ-12 в 2023 г.

Таблица 1

Результативность работы коммерческих банков в 2023 г.

Как видно из анализа, крупнейшим банком по величине активов является ПАО «Сбербанк», активы которого составляют 44,5 трлн руб., затем следует Банк ВТБ (ПАО) с 22,3 млрд руб. Третьим банком, активы которого превысили среднее значение 9,1 трлн руб., выступает Банк ГПБ (АО) с активами 13,6 трлн руб. Замыкает список банков, вошедших в Топ-12 по итогам работы в 2023 г., АО Тинькофф Банк с активами 1,6 трлн руб. (рис. 1).

Анализ показал, что в суммарном выражении по итогам 2023 г. коммерческие банки, вошедшие в Топ-12, имеют активы, доля которых составляет 80,7 % от активов всей банковской системы РФ. Таким образом, устойчивость российской банковской системы во многом определяется устойчивостью рассматриваемых банков. В тройке лидеров с соответствующими долями активов: ПАО «Сбербанк» – 33,0 %, Банк ВТБ (ПАО) – 16,5 %, Банк Газпромбанк (АО) – 10,1 % [3].

Замыкает рейтинг АО «Тинькофф Банк», доля активов которого составляет 1,2 % (табл. 1).

Важно выявление закономерностей в сложившейся ситуации в российском секторе, с использованием различных методов, в частности метода кластерного анализа. На практике часто применяют четыре метода обучения без учителя с целью получения визуализации данных посредством кластеризации с использованием языка Python [4]. В настоящей статье были использованы два из них. Целесообразно применять обучение без учителя (unsupervised learning), что позволяет использовать возможности алгоритма по поводу проведения разметки данных. Как известно, обучение без учителя есть не что иное, как класс методов машинного обучения, который позволяет выявить закономерности в изучаемом массиве данных. Очень удобно, не имея меток “y” в обучающем множестве, используя «обучение без учителя», в конечном итоге получить размеченный массив данных, имеющих не только метки “X”, но и “у”, поскольку система самостоятельно проведет подбор путем поиска шаблона в имеющихся примерах, опираясь на алгоритм.

Результаты исследования и их обсуждение

1. Кластерный анализ с использованием метода k-средних

Среди экспертов бытует мнение, что метод k-средних вполне применим как алгоритм кластеризации для автоматизации процесса разметки неразмеченного набора данных, поскольку основан на формировании некоторой совокупности точек кластеров, которые выбираются вокруг некоторых случайно выбранных точек, называемых центроидами, при соблюдении принципа минимизации суммарных квадратичных отклонений.

Для формирования датасета поля таблицы исходных данных для удобства были переименованы: Активы, трлн руб. – Assets; Доля активов, в % к итогу – Share of assets; Прибыль, млрд руб. – Net profit; Рентабельность активов, % – Return on assets (табл. 2).

Таблица 2

Датасет нейросети для кластерного анализа (фрагмент)

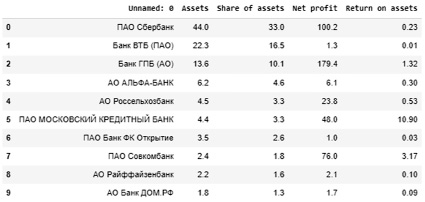
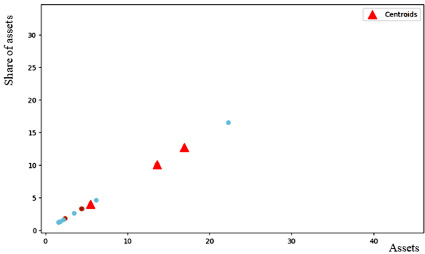
Рис. 2. Центроиды сформированных кластеров, полученных на основе параметров Топ-12 российских банков по критериям Assets и Share of assets

В целях проведения исследования методом k-средних необходимо выполнить некоторые действия. В частности, вначале определить, сколько кластеров будет формировать алгоритм, например, может быть установлен параметр модели n_clusters, равный некоторому целому числу. В нашем примере были сформированы три кластера. Далее алгоритм случайным образом выбрал три точки, которые стали центрами кластеров – центроидами. Затем алгоритм добавляет точки, осуществляя поиск «ближайших соседей» относительно каждого из имеющихся центроидов и происходит перерасчет местоположения центроидов, с поправкой на координаты новых точек. Как только координаты центроидов перестают меняться, алгоритм прекращает свою работу. Следует отметить, что полученные координаты центроидов в каждом из кластеров отражают некоторые усредненные параметры сформированных кластеров.

Разделение данных на кластеры происходит на основе имеющихся характеристик, а предсказание свойств основано на том, к какому кластеру может принадлежать пример. Эксперты склоняются к мнению о том, что это метод кластеризации является наиболее востребованным и широко применяемым среди известных алгоритмов машинного обучения.

Цель кластеризации обычно сводится к отбору и выделению некоторых параметров, обладающих некоторыми похожими чертами, причем процесс происходит при отсутствии такого разбиения. Финальной целью является предсказание степени соответствия объектов выборки их классам на основе сформированных кластеров. Центроиды сформированных кластеров, полученных на основе параметров Топ-12 российских банков, отмечены на гистограмме (рис. 2).

Как следует из логики алгоритма, происходит случайным образом выбор центров кластеров, и затем алгоритм старается минимизировать функцию потерь. Следует указать на один недостаток при использовании такого подхода. В том случае, если центры кластеров выбираются относительно близко друг к другу, то алгоритм часто разделяет то, что должно быть единым кластером, и при этом может «объединить» два разных.

2. Иерархическая кластеризация с применением искусственного интеллекта

Использованная в исследовании иерархическая кластеризация представляет собой алгоритм, основанный на применении искусственного интеллекта, который имеет своей целью формирование кластеров, что оказывается весьма целесообразным при поиске закономерностей в больших массивах данных. В отличие от метода k-средних, иерархическая кластеризация упорядочивает исходный массив таким образом, что каждое значение в конечном счете получает отдельный кластер. После чего происходит объединение ближайших кластеров в один – и так до тех пор, пока не сформируется общий кластер, как правило, его представляют в виде дендрограммы (рис. 3).

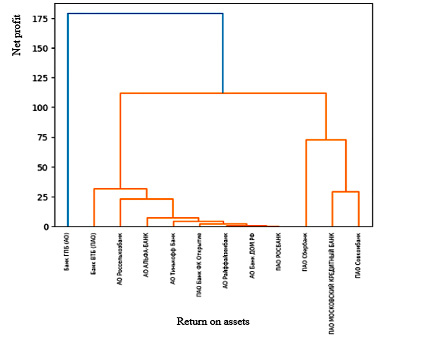
Рис. 3. Дендрограмма иерархической кластеризация банков по Net profit и Return on assets

Дендрограмма обеспечивает визуализацию ранжирования по кластерам по уровню параметра рентабельность активов от минимальных значений у гигантов с низкой рентабельностью ПАО ГПБ (АО) – 1,32 % и Банк ВТБ (ПАО) – 0,01 %, до мелких по размеру, но высокорентабельных ПАО «Совкомбанк» – 3,17 % и ПАО «Московский кредитный банк» – 10,9 %.

3. Анализ с применением ML-модели «Случайный лес»

Формирование DL-модели происходит с использованием библиотек pandas, matplotlib.pyplot, sklearn, LinearRegressio, RandomForestRegressor. Формирование DL-модели происходит в четыре этапа: 1) создание случайных выборок из заданного набора данных; 2) построение для каждой выборки дерева решений и получение результата предсказания при использовании данного дерева; 3) проведение голосования за каждый полученный прогноз; 4) выбор предсказания с наибольшим количеством голосов в качестве окончательного результата.

Работа DL-модели «Случайный лес» может быть настроена с помощью гиперпараметров, если использовать библиотеку GridSearchCV. Фрагмент датасета для прогноза чистой прибыли для использования ML-модели «Случайный лес» представлен в табл. 3.

Для разделения данных на обучающее и тестовое множества случайным образом, с заданным соотношением, например 0,20, была использована библиотека model_selection Scikit-Learn, которая содержит метод train_test_split.

Важную роль играет правильный подбор гиперпараметров, который может быть выполнен с помощью функции GridSearchCV. В процессе работы алгоритма происходит последовательный перебор сочетаний вариантом и из общей совокупности (ансамбля) деревьев решений выбирается лучшее. В ходе исследования были заданы три параметра количества деревьев n_estimators: 5, 10 и 50. Следующим параметром выступали три критерия: squared error, absolute error, poisson. Кроме того, при подборе гиперпараметров использовалась настройка – максимальная глубина деревьев max depth: 2, 5, 10. В результате работы алгоритма был получен некоторый результат «лучшее дерево», имеющий минимальные значения ошибки, оно имело следующие настройки гиперпараметров: количества деревьев – 5, максимальная глубина дерева 10 уровней. Визуализация лучшего дерева представлена ниже (рис. 4).

Величина чистой прибыли банков является результативным признаком, который был обозначен как target. После удаления ненужного столбца (названий банков) датасет принял рабочий вид. Использование библиотеки lin_reg.coef позволяет рассчитать матрицу парных коэффициентов корреляции и сформировать уравнение многофакторной линейной регрессии, что позволит сделать прогноз величины прибыли рассматриваемых банков на следующий тайм фрейм.

Таблица 3

Фрагмент датасета для ML-модели «Случайный лес»

Если обозначить исходные параметры: Х1 – Активы, трлн руб., Х2 – Доля активов в % к итогу, Х3 – Рентабельность активов, % и У – Прибыль, млрд руб., уравнение регрессии примет вид

У = –11,8562 – 219,273 × Х1 + 298,353 × Х2 + 22,764 × Х3. (1)

Величины парных коэффициентов корреляции указывают на то, что связь положительная и средняя у факториальных признаков Х1 +0,440; Х2 +0,441 и слабая у Х3 + 0,212.

Качество сформированной DL-модели характеризуется следующими параметрами: Средняя абсолютная ошибка (MAE – Mean Absolute Error): 92,3073713994; Среднеквадратическая ошибка (MSE – Mean Squared Error): 15409,114181908903 и Среднеквадратическое отклонение (RMSE – Root Mean Squared Error): 124,13345311361036.

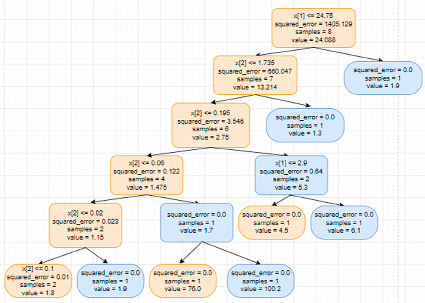
Рис. 4. Лучшее дерево DL-модели «Случайный лес»

Рис. 5. Вектор параметров DL-модели для получения прогноза

Как показывает практика, использование таких моделей «Случайного леса» приемлемо для решения широкого круга задач, ввиду его гибкости и практичности. Модель машинного обучения «Случайный лес» с успехом может быть использована для прогнозирования, классификации, а также отбора ряда признаков, причем как прикладных задач отдельного предприятия или отрасли в целом, так и для научных задач, связанных с поиском закономерностей в массивах больших данных. Нейросетевой алгоритм DL-модель «Случайный лес» не может быть переучена в силу специфики применяемого алгоритма, а также превосходит по точности прогноза отдельное «Дерево решений», поскольку благодаря использованию гиперпараметров может генерировать обширную совокупность, «ансамбль» деревьев, из числа которых выбирается лучшее.

В целях формирования прогнозного значения величины чистой прибыли для ПАО «Сбербанк» на следующий год, был сформирован вектор для подстановки в DL-модель (рис. 5).

Прогнозное значение для Сбербанка при прочих равных условиях – по данным 2022 г. составило 81,38 млрд руб. при фактически достигнутом 100,2 млрд руб., т.е. ожидаемая чистая прибыль может оказаться в 2023 г. на 18,7 % меньше. Алгоритм «Случайного леса» не переучивается, в отличие от остальных нейросетей, минимизируя таким образом шансы допущения неточности, то есть большое количество отдельных деревьев будут работать точнее, чем одно отдельное дерево.

Как показывает практика, использование систем искусственного интеллекта очень важно в современных условиях. Рассмотренные модели имеют как определенные преимущества, так и недостатки. Представляется целесообразным в перспективе расширить как перечень рассматриваемых параметров, которые бы отражали процесс развития и усиление устойчивости, так и временной горизонт. Важно опираться на широкие возможности систем искусственного интеллекта, не только ML «Случайного леса», но и глубоких сверточных нейронных сетей, таких как: CNN – сверточная нейронная сеть (ConvNet/CNN), которая представляет собой алгоритм глубокого обучения, RNN – рекуррентная нейронная сеть (RNN), представляющая класс нейронных сетей, которые успешно используются для прогнозирования последовательных данных, таких как временные ряды и др.

Результаты, полученные современными российскими и зарубежными исследователями, свидетельствуют о том, что отдельные аспекты затронутой проблемы требуют проведения дальнейших научных исследований. Как известно, алгоритм «дерево решений» находит широкое применение для решения множества различных практических задач. Это совершенно справедливо и для алгоритма «Случайного леса», поскольку многие ученые широко используют в своих исследованиях, например, Г. Лoуппе и др. [5]. По мнению Бреймана, классической разновидностью является бинарное дерево классификации, которое представляет собой некоторую модель, имеющую выраженную древовидную структуру Т из случайного входного вектора (Х1–Хр). [6] Отдельные авторы: A. Bril и др. [7], S. Demidova с коллегами [8] и I. Ilin [9] – отмечают, что налицо особенности процессов протекания сегментации и позиционирования в нейросетевой экономике. Исследователи приходят к выводу, что особенности процессов сегментации и позиционирования в нейросетевой экономике во многом обусловлены такими факторами, как прикладные вычисления, компьютеры и бизнес.

Как показывает практика, все более широкое применение находят когнитивные модели. В частности, Н.И. Ломакиным и его коллегами сформирована когнитивная модель, с помощью которой можно подготовить данные и, применяя нейросети, получить прогноз финансовой устойчивости отечественной экономики в условиях рыночной неопределенности и усиления всех видов риска. [10]

Заключение

На основе вышеизложенного можно сделать определенные выводы.

Большое значение в современных условиях имеет исследование проблем развития не только реального сектора экономики, но и отечественной банковской сферы и выявление путей, обеспечивающих их устойчивое развитие. В основе устойчивости российской банковской системы лежит устойчивое развитие ведущих банков. В тройке лидеров с соответствующими долями активов: ПАО «Сбербанк» – 33,0 %, Банк ВТБ (ПАО) – 16,5 %, Банк Газпромбанк (АО) – 10,1 %. Среди известных методов кластеризации можно отметить алгоритмом кластеризации данных метод k-средних. Такой подход имеет один недостаток. Центры кластеров могут быть выбраны слишком близко друг к другу, в этом случае алгоритм может разделить совокупность, которая могла бы образовать единый кластер, и объединить два разных. Результат иерархической кластеризации представлен с помощью дендрограммы, которая обеспечивает визуализацию ранжирования в кластерах по уровню параметра рентабельность активов от минимальных значений у гигантов с низкой рентабельностью ПАО ГПБ (АО) – 1,32 % и Банк ВТБ (ПАО) – 0,01 %, до мелких по размеру, но высокорентабельных ПАО «Совкомбанк» – 3,17 % и ПАО «Московский кредитный банк» – 10,9 %. В результате использования разработанной системы искусственного интеллекта МL-модели получено прогнозное значение чистой прибыли для Сбербанка. При прочих равных условиях, по входным параметрам 2022 г. прогноз составил 81,38 млрд руб. при фактически достигнутом значении 100,2 млрд руб., то есть ожидаемая чистая прибыль может оказаться в 2023 году на 18,7 % меньше.