Наука и практика управления финансами предложили различные методы оптимизации инвестиционного портфеля предприятия, которые охватывают различные аспекты, такие как максимизация доходности, минимизация риска и поиск оптимального баланса между ними.
Обзор научной литературы отражает наличие большого числа подходов к формированию и оптимизации инвестиционного портфеля [1, с. 6, 11-18; 2].
Теории оптимизации портфеля могут быть сгруппированы по различным критериям (методологии, принципу рациональности инвестора, фокусу на различных аспектах инвестиционного процесса и др.). Группировка теорий может изменяться в зависимости от подходов и акцентов в контексте инвестиционного анализа. Согласно нашему мнению, можно выделить следующие группы:
1. Теории рационального поведения инвестора. В эту группу входят классическая теория оптимизации портфеля, основанная на работах Г. Марковица, теория CAPM и др. Предполагается, что инвесторы принимают рациональные решения, оптимизируя свой портфель с учетом доступных рыночных данных и своих предпочтений в отношении риска и доходности.
2. Поведенческие теории, которые включают в себя аспекты, связанные с нерациональным поведением инвесторов, учитывают эмоциональные и психологические факторы, влияющие на инвестиционные решения. Теории поведенческой финансовой экономики рассматривают, например, аномалии рынка и переоценку активов.
3. Факторные модели и арбитражная теория ценообразования (далее АРТ). Эти теории сосредотачиваются на факторах риска, которые могут влиять на доходность активов. Но между ними есть отличия, факторные модели включают в себя большой перечень факторов рынка, таких как стоимость капитала, размер компании, стоимость акций и др., а APT, с другой стороны, предполагает, что активы должны оцениваться с учетом определенных факторов риска, а их цены корректироваться в соответствии с ожидаемой доходностью.
Несмотря на то что существует достаточно много методов к оптимизации инвестиционного портфеля, разработка нового подхода в современных условиях оправдана быстрыми изменениями на финансовых рынках, необходимостью учета сложных взаимосвязей между его участниками, появлением новых классов активов, цифровых финансовых инструментов [3], возможностью использования преимуществ современных технологий [4].
Целью исследования является разработка методики оптимизации портфеля инвестиций, базирующейся на математической модели и алгоритме, что позволит эффективно управлять финансовыми активами предприятия в условиях санкционных ограничений и повышенного уровня финансового риска.
Материалы и методы исследования
В основе методики лежит математическая модель, предназначенная для оптимизации портфеля инвестиций, учитывая целый ряд параметров, таких как ожидаемая доходность активов, корреляции между ними и ограничения по риску. Для решения данной задачи используются машинное обучение (в частности, LSTM для временных рядов), генетический алгоритм, который обеспечивает эффективное и быстрое нахождение оптимального соотношения активов в портфеле предприятия.
Методика базируется на наиболее адаптивных и современных методах оптимизации инвестиционного портфеля, таких как теория Марковица, генетические алгоритмы, машинное обучение.
Результаты исследования и их обсуждение
Для разработки методики проведен качественный сравнительный анализ существующих и наиболее известных методов оптимизации инвестиционного портфеля. Сравнительная оценка методов представлена в таблице.
Разработанный Г. Марковицем метод впервые представлен в его статье 1952 г. Согласно методу, предлагается оптимизировать портфель посредством нахождения оптимального соотношения активов, которое обеспечивает максимальную доходность при заданном уровне риска или минимальный риск при заданной доходности [5].
Метод Роя – Шарпа (Sharpe’s Single Index Model), разработанный У. Шарпом, предлагает упрощенный способ оптимизации портфеля, сосредотачивая внимание на систематическом риске и рассматривая активы относительно одного фактора риска, как правило, рыночного индекса [6].
КАПМ-модель (Capital Asset Pricing Model) оценки доходности активов включает в себя расчет ожидаемой доходности актива с учетом его систематического риска, как правило, для определения оптимального соотношения между рискованными и безрисковыми активами в портфеле [6].
Метод Линдера (Linder’s Model) ориентирован на оптимизацию портфеля посредством нахождения баланса между долями облигаций и акций, учитывая корреляцию между ними, а также взаимосвязь доходности и риска.
Методы формирования инвестиционного портфеля с использованием квадратичного программирования широко используются на практике для решения задачи по его оптимизации с квадратичной целевой функцией и линейными ограничениями.
Метод Брутто (Brinson Model) фокусируется на активном управлении портфелем, измеряя вклад каждого актива в общей доходности.
Метод Блэка – Литтермана (математическая модель распределения активов в портфеле), предложенный сотрудниками компании «Голдман Сакс» Ф. Блэком и Р. Литтерманом в 1990 г., основан на комбинации теории Марковица и оценки систематического риска. Этот метод позволяет адаптировать портфель к текущим рыночным условиям.
Сравнительная оценка методов оптимизации инвестиционного портфеля
|
Метод оптимизации инвестиционного портфеля |
Сущность |
Преимущества, достоинства метода |
Ключевые недостатки |
|
Теория Марковица (1952) |
Используются комбинации активов для построения эффективного соотношения доходности и риска |
Прост в реализации, помогает инвесторам выбирать оптимальные портфели в зависимости от их предпочтений по риску и доходности |
Предполагает, что доходности и риски активов стабильны и могут быть точно измерены |
|
Модель Роя – Шарпа (1963) |
Рассматривает активы относительно одного фактора риска, обычно рыночного индекса |
Прост в использовании, учитывает систематический риск |
Может недооценивать диверсификацию и не учитывает все виды рисков |
|
Капиталовложения по модели КАПМ (CAPM) (1964) |
Связывает ожидаемую доходность актива с его систематическим риском |
Предоставляет метод оценки доходности активов, учитывая их систематический риск |
Основан на предположении о рациональном поведении инвесторов и стабильности коэффициентов бета |
|
Модель Линдера (1973) |
Оптимизирует портфель с учетом корреляции между акциями и облигациями |
Учитывает разнообразие активов в портфеле |
Может требовать большого объема данных и сложных вычислений |
|
Квадратичное программирование (1970-е гг.) |
Решает задачу оптимизации с квадратичной целевой функцией и линейными ограничениями |
Обеспечивает точное решение для многих задач оптимизации портфеля |
Может быть вычислительно затратным для больших портфелей |
|
Метод Брутто (1986) |
Измеряет вклад каждого актива в общую доходность портфеля |
Учитывает активное управление портфелем |
Требует оценки вклада каждого актива, что может быть сложным |
|
Метод Блэка – Литтермана (1992) |
Комбинирует ожидания инвесторов с результатами модели портфеля Марковица |
Улучшает оценки активов с учетом внешних ожиданий |
Может быть сложным для применения без точных данных о предпочтениях инвесторов |
|
Метод Дженкинса (1999) |
Акцент на адаптивном изменении весов активов |
Учитывает динамику рынка |
Может быть менее точным при условии ограниченности данных |
|
Генетические алгоритмы (1990-е гг.) |
Применение эволюционных методов для оптимизации портфеля |
Гибкость, способность к обработке больших объемов данных |
Требует параметризации и может потребовать много времени на вычисления |
|
Алгоритмические методы (2000-е гг.) |
Использование различных оптимизационных алгоритмов, включая методы машинного обучения |
Адаптивность к сложным условиям рынка |
Требует больших вычислительных ресурсов и данных |
|
Метод экстремальных квантилей (2000-е гг.) |
Ориентирован на минимизацию максимальных возможных потерь |
Учитывает экстремальные сценарии |
Требует точной оценки квантилей распределения |
|
Статистические методы (применение временных рядов, 2000-е гг.) |
Применение статистических методов для прогнозирования доходности активов |
Учитывает динамику изменений в рыночных условиях |
Может быть сложным в применении при ограниченных данных |
Источник: составлено автором.
Метод Дженкинса базируется на идеях оптимального управления портфелем, включая адаптивное изменение весов активов в зависимости от рыночных условий.
В области вычислительной оптимизации применяются генетические алгоритмы для поиска оптимальных портфелей, которые основаны на эволюционном подходе к оптимизации портфеля, эмулируя естественный процесс отбора и мутаций.
Алгоритмические методы включают в себя применение различных оптимизационных алгоритмов, таких как методы глобальной оптимизации, эволюционные алгоритмы и методы машинного обучения для поиска оптимальных портфелей [7].
Метод экстремальных квантилей (Extreme Quantile Optimization) нацелен на учет различных экстремальных (критических) сценариев и минимизацию потерь в таких условиях. Его разновидностью можно считать метод «Минимакс» (Minimax Method), ориентированный на минимизацию максимальных возможных потерь, главная цель – сформированный портфель не приведет к экстремальным убыткам в текущем периоде [8, с. 88, 112].
В современных условиях не существует однозначно устаревших методов оптимизации портфеля, поскольку эффективность метода может зависеть от многих факторов, включая характеристики рынка, степень доступности данных, финансовые цели инвестора и др. Однако некоторые методы могут считаться менее применяемыми в определенных ситуациях или требовать дополнительной модификации для учета современных тенденций и условий рынка. Считаем, что в современных условиях метод Марковица может не всегда точно предсказывать будущие доходности и риски активов; метод КАПМ (CAPM) предполагает стабильность коэффициента бета, что может быть недостаточно обоснованным в настоящее время; модель Линдера ориентирована на комбинацию из облигаций и акций, что затрудняет процесс приобретения других видов активов, таких как криптовалюты или иные финансовые инструменты. Методы, ориентированные только на один тип рисков (например, систематические риски), могут недооценивать полный спектр рисков в современных сложных рыночных условиях.
Считаем, что современные методы оптимизации инвестиционного портфеля должны включать в себя применение искусственного интеллекта (например, машинное обучение), поэтому в основу разработанной методики легли принципы метода Марковица для построения эффективного фронта на основе ожидаемых доходностей активов и ковариаций активов, а также механизмы построения генетических алгоритмов и инструменты машинного обучения (например, LSTM для временных рядов), которые позволяют прогнозировать будущие доходности активов на основе исторических данных.
Сущность предлагаемой методики в том, что генетические алгоритмы применяются для оптимизации весов активов в портфеле с учетом прогнозов с помощью метода Марковица и машинного обучения. Методика предполагает учет индивидуальных предпочтений и рискового профиля инвестора.
Целевой функцией является максимизация ожидаемой доходности портфеля при заданном уровне риска.
Для более консервативных инвесторов целевой функцией может стать минимизация риска посредством учета ковариаций активов для минимизации общего риска портфеля.
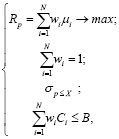
где Rp – ожидаемая доходность портфеля;
wi – вес актива i в портфеле;
μi – ожидаемая доходность актива;
σp – стандартное отклонение (риск) портфеля;
N – количество активов в портфеле;
X – заданный (предельный) уровень риска инвестиционного портфеля согласно рисковому профилю компании как инвестора;
Ci – стоимость актива i;
B – бюджет компании, доступный для инвестирования.
Уровень риска портфеля предлагается оценивать по формуле:
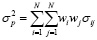 ,
,
где σij – ковариация между доходностями активов i и j;
μi определяется на основе прогнозов доходности от LSTM модели для актива i.
Определение предельных значений допустимых рисков при инвестировании должно осуществляться в соответствии с рисковым профилем компании как инвестора, ее финансовых возможностей, на основе оценки денежных потоков за продолжительный период времени, с учетом специфики самого предприятия и отрасли. Как правило, уровень предельных (допустимых) рисков устанавливается экспертным путем.
Оптимизация весов wi осуществляется с помощью генетического алгоритма.
Эта математическая модель отражает основные компоненты методики – максимизацию ожидаемой доходности, учет ковариаций активов, установление ограничений на веса активов и риск портфеля, а также интеграцию прогнозов от модели машинного обучения и генетического алгоритма для оптимизации весов активов в портфеле предприятия.
LSTM – это часть семейства рекуррентных нейронных сетей (RNN), которые применяются в области обработки последовательностей данных, таких как временные ряды. Лучший способ получить модель LSTM, которая соответствует вашим потребностям, – это обучить ее на своих собственных данных.
Разрабатываются они по следующему алгоритму:
− подготавливается временной ряд исторических цен активов для программирования LSTM модели;
− модель тестируется на тестовой выборке для оценки ее способности обобщения данных, в процессе используются метрики, такие как Mean Squared Error (MSE) или другие, для оценки точности прогнозов;
− после успешного обучения и тестирования модели LSTM она может быть использована для генерации прогнозов доходности каждого актива.
Данная модель позволяет осуществлять регулярное обновление портфеля (каждый квартал/месяц) с учетом новых данных, введение персонализированных параметров в модель для учета инвесторских предпочтений и ограничений.
Заключение
Предлагаемая методика является адаптивной моделью к изменениям на финансовом рынке. Использование прогнозов с применением машинного интеллекта позволяет повысить точность оценки будущих доходностей активов.
Методика не лишена некоторых недостатков, метод требует доступа к большому объему данных и вычислительным ресурсам, однако применение современных цифровых инструментов позволяет разрешить эти проблемы.



