Весовые коэффициенты (ВК) широко используются при решении широкого класса задач в самых различных областях науки и техники. Особенно велика их роль при моделировании многофакторных объектов и сложных иерархических систем, в которых влияющие на конечный результат факторы играют различные роли, что чаще всего и бывает в исследованиях реальных объектов [1, с. 42].
ВК представляют собой строго положительные числа, сумма которых равна 1 или 100 %:
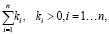
где n – число ВК.
Каждому фактору присваивается соответствующий коэффициент. В научной литературе можно встретить и другие определения ВК, но в таких случаях они могут совпадать с другими числовыми коэффициентами, в частности коэффициентами значимости, которые также могут иметь значения от долей процента до 100 %, но не равны этой сумме. Есть у них и другие различия. Так, например, классическая математическая модель биологического нейрона, используемая при построении нейронных сетей, допускает наличие синапсов как с положительными, так и с отрицательными весами. В ней в поступающем к нейрону суммарном импульсе
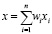
где wi – веса синапсов, xi – силы поступающих к синапсам импульсов, синаптические связи с положительными весами считаются «возбуждающими», с отрицательными – «тормозящими» [2, с. 10]. Еще один пример использования отрицательных весов можно встретить в портфельной теории для так называемых «плохих» активов, когда при помощи метода портфельного котирования PQM инвестиционный портфель разделяется на две части – «хорошую» и «плохую» [3, с. 4530].
Содержательно ВК используются в задачах, связанных с относительным распределением какого-либо ресурса, вклада в формирование результата и т.д., когда эту долю или вклад проблематично оценить в абсолютных (натуральных) величинах. В качестве примера здесь можно привести распределение полезностей в предложенной академиком В.Л. Макаровым модели социального планирования [4, с. 8].
Чаще всего ВК используются при решении классификационных задач. ВК также используются как коэффициенты при оценке экономической безопасности в прогностических экономических задачах [5, с. 80], несмотря на то, что такой подход вызывает множество вопросов. Весовые коэффициенты также используются в численных схемах решения задач радиолокации [6, с. 56], цифровой фильтрации данных [7, с. 5], технике [8, с. 245], аналитических [9, с. 64] и, как уже упоминалось выше, нейронных сетях [10, с. 55] и во многих других областях. В общем, сфера их применения достаточно широка, что неудивительно. Например, В.Л. Макаров и А.Р. Бахтизин в своей книге, посвященной агент-ориентированным моделям сложного мира, отмечают, что в каждой области человеческой деятельности существуют знания, которые трудно формализовать математическими формулами, что и обусловило появление экспертных систем [11, с. 52]. Но тем не менее для представления знаний специалиста-эксперта с целью их последующей компьютерной обработки так или иначе требуется их оцифровка, одним из методов которой стало применение ВК.
Вместе с тем нахождение ВК для последующего применения их в моделях представляет, как совершенно верно отметил академик Н.Я. Петраков, самостоятельную задачу, выходящую за рамки моделирования [12, с. 130]. Такое отношение к ВК (в скобках отметим, что и к другим числовым коэффициентам, например коэффициентам значимости) вполне оправдано и обусловлено тем, что для их нахождения необходимо применить ряд специальных процедур, которые не входят в сам процесс моделирования.
Наиболее часто для этого применяются экспертные технологии, в основе которых лежит опрос экспертов. Непосредственно вычислить ВК возможно лишь в тех случаях, когда для этого имеется достаточное количество исходных данных, качество которых (достоверность, точность, полнота, аутентичность, релевантность и т.д.) не вызывает сомнения. Тогда можно использовать как апробированные статистические методы – частота повторяемости и регрессии [13, с. 72], так и специально разработанные методы, такие как, например, различные модификации метода ближайших соседей [14, с. 117].
Авторы более четверти века применяют весовые коэффициенты при решении задач принятия стратегических решений социально-экономического и эколого-экономического характера (в том числе касающихся вопросов районирования территорий и акваторий). При использовании разных методов их вычисления и процедур проведения экспертных опросов накопился определенный опыт, обобщенный в ряде публикаций и монографий [15, с. 95; 16, с. 92–148]. Тем не менее некоторые аспекты применения различных методов в практических приложениях остались недостаточно освещенными. Поэтому целью данного исследования является обзор и систематизация полученных ранее разрозненных результатов с выделением положительных и отрицательных сторон каждого из рассматриваемых экспертных методов вычисления весовых коэффициентов влияющих факторов в социальных и эколого-экономических исследованиях.
Материалы и методы исследования
Информационную основу исследования составили многочисленные научные труды отечественных и зарубежных ученых, посвятивших свои исследования как общим вопросам применения экспертных методов и технологий в науке, так и их частным случаям для решения отдельных прикладных социальных, экономических и экологических задач. Авторами был использован системный подход, компаративный и логический виды анализа, статистический анализ данных, полученных в результате собственных исследований при проведении экспертных опросов.
Результаты исследования и их обсуждение
Из множества экспертных методов нахождения ВК рассмотрим наиболее часто встречающиеся на практике, а именно: прямую расстановку, ранжирование и попарные сравнения. В последнем случае выберем один из самых популярных методов – метод анализа иерархий, предложенный и развитый американским ученым Томасом Саати [9, с. 34; 17, с. 23].
Прямая расстановка. Наверное, самый первый из методов экспертного оценивания. Суть его состоит в том, что каждому фактору непосредственно присваивается число, представляющее собой долю единицы при обязательном условии равенства их суммы единице. Не воспрещается двум и более факторам присваивать одинаковые веса. При этом большинство авторов полагает, что неважно, в каком порядке расположены факторы перед началом оценивания. С этим не согласен А.Е. Любарев, исследовавший смещение оценок избирателей [18, с. 2] и утверждающий, что стоящие вверху списка партии при голосовании получают на 1–2 % больше, чем было бы, если бы они находились ниже. Но свои результаты он получил при массовых опросах, каковыми по своей сути являются выборы, в то же время пока неизвестно, как порядок расположения в списке влияет на работу экспертов.
Ранжирование. От экспертов требуется построить ранжированный ряд, т.е. расположить факторы в порядке возрастания или убывания их значимости. При этом они так же, как и в предыдущем методе, могут двум и более факторам присваивать одинаковый ранг.
ВК ki рассчитываются по простой формуле
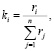
где ri, rj – ранги, i, j = 1,…,n – номера факторов.
Если же ранги объединяются, то берется среднее арифметическое значение из объединенных рангов. Так, при n = 5 вектор ВК будет k = (0,067; 0,133; 0,200; 0,267; 0,333). Как легко убедиться, сумма этих ВК равна 1. Если бы эксперт придал первым двум факторам равное значение, то они получили бы ранг 1,5, что соответствовало бы ВК, равному 0,100. То же значение было бы получено при усреднении самих ВК: (0,067 + 0,133) / 2 = 0,100.
При использовании этой формулы есть одна особенность, незнание которой может привести к грубой ошибке. Дело в том, что обычно наиболее значимые ранги соответствуют началу натурального ряда чисел. Это означает, что первый ранг будет наиболее значимым. Так, например, составлена знаменитая Табель о рангах Российской империи, в соответствии с которой наиболее высокому первому классу соответствовали чины канцлера для гражданских лиц и генерал-фельдмаршала и генерал-адмирала для военных. Если не учитывать это обстоятельство, то результат будет противоположным: наиболее значимые факторы получат наименьшие ВК. Чтобы этого не произошло, результаты ранжирования необходимо развернуть в обратную сторону, т.е. наиболее высокие ранги должны соответствовать наиболее значимым факторам.
При групповой экспертной оценке возникает задача построения результирующего ранжирования, для решения которой необходимо уметь определять «меру близости» между ранжированиями, выполненными различными экспертами. В качестве такой меры могут быть использованы самые различные метрики. Например, для целей групповой экспертной оценки сравнительной эффективности крупномасштабных инвестиционных проектов в работе [19, с. 75] для определения «близости» ранжировани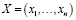й 
и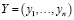 
авторы предлагают использовать метрику Кемени
,
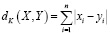а в качестве результирующего ранжирования – медиану M множества ранжирований X, полученную из соотношения
.
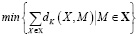Однако здесь могут быть свои «подводные камни». Предположим, что два эксперта проранжировали две альтернативы как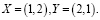 
Расстояние Кемени между этими ранжированиями равно 2, других ранжирований нет, поэтому в качестве медианы может быть принято как ранжирование X, так и Y.
Попарное сравнение. В этих методологиях объекты – в целом или по компонентам – сравниваются попарно. Процесс производится последовательно – каждый объект, его компонент или влияющий фактор сравниваются друг с другом. Всего производится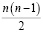 
попарных сравнений, где n – число сравниваемых объектов (компонентов, факторов). При этом влияние на них других членов не учитывается. Степень влияния оценивается по специальной вербально-числовой шкале.
В результате получается квадратная обратно-симметричная матрица с единичной диагональю, поскольку сравнение с самим собой тождественно.
Положительные и отрицательные стороны рассмотренных методов
Прямая расстановка. Положительными сторонами этого метода являются его простота и непосредственность: результат получается быстро и сразу. Наиболее существенным недостатком (отрицательные стороны метода) является количество одновременно оцениваемых факторов, которое ограничено так называемым числом Ингве, равным 7±2 – среднему объему оперативной памяти человека [20, с. 158], да и то, как установил академик О.И. Ларичев, при соответствующем тренинге экспертов [21, с. 132]. И, по-видимому, не случайно именно такое количество интервалов, как оптимальное, часто рекомендуют для разработки шкал, предназначенных для измерения процессов в психологии [22, с. 25].
Ранжирование. Этот метод также достаточно прост и не вызывает никаких трудностей в применении. Пожалуй, для экспертов это самый простой метод, поскольку им требуется расположить объекты в порядке убывания или возрастания их значимости, объединяя равнозначные объекты в одну группу, что также не вызывает трудностей. К тому же, как было установлено в ([23], цит. по [24, с. 79]), ранговые распределения в большинстве своем весьма устойчивы.
Отрицательные стороны. На точность определения ВК при ранжировании влияет дискретизация, зависящая от n – числа сравниваемых объектов (компонентов, факторов). При больших значениях n это не критично, но при малых значениях приводит к искажениям результатов, особенно в тех случаях, когда, по мнению эксперта, эти значения должны быть близкими. Но такие несоответствия можно устранить путем корректировки рассчитанных значений весовых коэффициентов, исходя из требования равенства суммы вносимых поправок нулю [25, с. 225]. Сочетание методов – обычная практика в методологиях, как, например, использование попарного сравнения с последующим ранжированием при анализе альтернатив [26, с. 127].
На первый взгляд может показаться, что это та же прямая расстановка. Но на самом деле это не так. Во-первых, как было отмечено выше, на прямую расстановку влияет число сравниваемых компонентов, а когда их становится более 10, то число итераций растет стремительно, а с ними растет и время опроса. Во-вторых, при ранжировании общая картина видна сразу, и требуются только некоторые уточнения, которые в большинстве своем осуществляются попарно, а это совсем разные вещи. Причем пары образуются по выбору эксперта. Так, если к компоненту, допустим, k2 добавляется 0,05, то убавиться может в любом другом – первом, третьем и т.д. При этом данную прибавку можно расщеплять, т.е. 0,02 убавить из одного компонента, 0,03 – из другого. Самое главное, что этот процесс легко контролируемый, в то время как в прямой расстановке требуются определенные усилия, чтобы данный процесс не вышел из-под контроля. А это не так просто, поскольку одновременно необходимо держать в голове несколько слагаемых.
При ранжировании может возникнуть эффект, получивший название rank reversal – «изменение ранга» [27, с. 228]. Появляется он при добавлении/исключении новых факторов при оценке объектов, когда новые и исключенные факторы меняют порядок приоритетов у «старых» или оставшихся [28, с. 72]. Это обстоятельство требует постоянного внимания к процедурам интерпретации результатов моделирования. Отметим также, что при проведении групповой экспертной оценки получение результирующего ранжирования с использованием, например, медианы Кемени является NP-трудной задачей [29, с. 38]. К тому же результат поиска медианы, как отмечалось выше, может быть и неоднозначным.
Попарное сравнение (МАИ). Этот метод, как и прямая расстановка, сразу ориентирован на конечный результат, т.е. сравнение производится по их влиянию на конечную цель опроса, что важно при интерпретации результатов и разработке схем оптимизации. В этот метод его автором «встроен» алгоритм определения качества работы эксперта, основанный на сравнении результатов опроса с неким идеальным экспертом. Это обстоятельство существенно упрощает жизнь организаторам опросов, поскольку им самим не приходится производить оценки качества, которые могут занимать много времени.
Но, как и во всех методах, есть в нем и отрицательные стороны, причем весьма неочевидные. Самая, на наш взгляд, главная из них – попарное сравнение в МАИ требует, чтобы объект был формализован как система, т.е. все его составляющие влияли друг на друга. Поэтому шкала отношений Саати не имеет нулевых значений, что означает наличие обязательных, причем взаимных связей. Но далеко не все объекты являются системами. И здесь возникает противоречие с провозглашенным Саати принципом создания МАИ о сопоставлении факторов по их влиянию на конечный результат, что не требует обязательной взаимной связи между компонентами объекта. Но это уже проблема, относящаяся к герменевтике и заслуживающая самостоятельного исследования [30, с. 44], поэтому авторы в настоящей статье ее касаться не будут.
Требование транзитивности, которое заложено в критерии качества работы экспертов, очень сильное и в экспертных опросах далеко не всегда выполняется [31, с. 64; 32, с. 292], а критерий качества работы эксперта, так называемое отношение согласованности, не совсем корректно [31, с. 64].
МАИ требует специального обучения экспертов. Хотя оно занимает не так уж и много времени – до 20–30 мин, но, как оказалось, далеко не все эксперты, даже очень высокой квалификации – доктора наук и профессора, могут его усвоить по подробной инструкции. А это исключает их из заочных анонимных опросов. Тем не менее и часть усвоивших этот метод способны его быстро забыть, особенно правила заполнения матрицы парных сравнений.
Таким образом, краткая сравнительная характеристика методов нахождения весовых коэффициентов влияющих факторов может быть представлена в виде таблицы.
Как можно видеть из таблицы, каждый из рассмотренных методов имеет свои преимущества и недостатки. Это естественно. Но важно здесь другое: как показала практика авторов, все они дают достаточно близкие результаты. Это не должно вызывать удивления, поскольку при экспертной оценке происходит сопоставление компонентов по степени их важности, а оно не зависит от метода, и конечные результаты весьма близки, а то и совпадают. Различия же в числовых значениях обусловлены главным образом алгоритмами обработки экспертных оценок.
Сравнение методов нахождения весовых коэффициентов влияющих факторов
|
№ |
Метод |
Положительные стороны |
Отрицательные стороны |
Когда лучше применять |
|
1 |
2 |
3 |
4 |
5 |
|
1 |
Прямая расстановка |
Прост в применении |
Ограничение на число оцениваемых факторов |
При числе факторов не более 5–7 |
|
2 |
Ранжирование |
Прост в применении. Неограниченное число факторов |
Дискретизация значений ВК, влияющих на адекватность экспертных оценок, что особо проявляется при малом числе факторов |
Без ограничений. Недостаток, вызванный дискретизацией, легко устраним |
|
3 |
Попарное сравнение (МАИ) |
Концентрирует внимание только на парах факторов, без требования одновременного соотношения их с остальными факторами |
Требует специального обучения. Обязательное требование транзитивности факторов, что не всегда выполнимо. Объект должен представлять собой систему |
При числе факторов не более 14–15 |
Примеры применения весовых коэффициентов влияющих факторов в социальных и эколого-экономических исследованиях
Несмотря на достаточную популярность рассмотренных выше методов нахождения весовых коэффициентов влияющих факторов, приведем лишь некоторые примеры, наиболее ярко, на наш взгляд, демонстрирующие их работоспособность в задачах социальной, экологической и сугубо экономической направленности, а также в междисциплинарных исследованиях, сочетающих в себе все три вектора научных целей.
Так, например, для социологического исследования, цель которого заключалась в совершенствовании методики оценки социального благополучия населения, авторы использовали метод ранжирования для определения весовых коэффициентов факторов социального благополучия (здоровье, материальное благополучие, субъективное благополучие, социальный капитал, окружающая среда, социальная защищенность, правовая защищенность, культурно-досуговая сфера, образование, благоустройство территории проживания, ассоциированность с территорией проживания) [33, с. 150–151].
В исследовании наших коллег из Северного (Арктического) федерального университета приводится пример расчета весовых коэффициентов ряда факторов геоэкологического риска при возможном аварийном разливе нефти (переходы через водотоки, водоемы и водоохранные зоны, заболоченность территории, состав горных пород, многолетнемерзлые грунты, почвенные условия) методом анализа иерархий [34, с. 65–67].
В исследовании по разработке модели комплексной социально-экономической оценки арктических муниципалитетов Архангельской области было предложено производить отбор и сравнительное взвешивание факторов влияния также с использованием хорошо известного и подробно описанного выше метода анализа иерархий [35, с. 451].
В работе зарубежных ученых, посвященной оценке устойчивости инфраструктурных проектов, что само по себе является междисциплинарной задачей, одновременно закладывалось несколько групп факторов (социальные, экономические и экологические), оказывающие влияние на принятие решения о реализации этих проектов, при этом были использованы как метод ранжирования [36, с. 443–444], так и нечеткие оценки [37, с. 110].
Заключение
Сформулируем основные выводы, имеющие непосредственное прикладное значение. Они хоть и носят субъективный характер, тем не менее могут обратить внимание исследователей при разработке экспертно-аналитических систем на рациональные методы расчета весовых коэффициентов.
Ни один из рассмотренных методов не имеет явного предпочтения перед другими. Но метод анализа иерархий требует значительно больше времени и накладывает некоторые жесткие ограничения на формализацию объекта, наиболее сильным из которых является представление объекта в виде системы, что далеко не всегда представляется возможным.
Несмотря на достаточно близкие результаты числовых значений оценок важности факторов, авторы отдают преимущество ранжированию [38, с. 213]. Этот метод не только прост в применении, но также позволяет улучшать значения весовых коэффициентов путем введения корректирующих поправок.