Проблема формирования конкурентоспособности выпускников вузов в соответствии с требованиями современного рынка труда сегодня актуальна как никогда. Прежде всего для экономического сектора.
Проблеме формирования конкурентоспособности выпускников экономических вузов посвящено достаточно много исследований [1, 2]. Мы разделяем точку зрения исследователей, что в современных условиях (последствия пандемии COVID-19, Специальная военная операция ВС РФ, технологический суверенитет РФ) в российской экономике имеется острая потребность в конкурентоспособных специалистах, уровень подготовки которых соответствует профессиональным стандартам, обеспечивает мобильность и гибкость на рынке труда.
Мы согласны с мнением Е.В. Котляр, Е.М. Пушкаревой в части наиболее важных составляющих понятия «конкурентоспособность» – профессиональные знания и умения, личные качества (стрессоустойчивость, целеустремленность, инициативность и пр.), способность к эффективной деятельности на практике [3].
Учитывая вышесказанное, под конкурентоспособностью выпускника экономического вуза будем понимать способность адаптироваться к быстро изменяющимся социально-экономическим условиям и грамотно строить карьеру. В качестве средства формирования конкурентоспособности студентов рассмотрим потенциал экономико-математического моделирования в процессе предметной математической подготовки.
Обращаясь к характеристике термина «модель», происходящего от латинского modulus (мера, образец), важно отметить наличие различных подходов к определению понятия. Под математической моделью будем понимать формализованный образ объекта, генерирующий наиболее важные черты и используемый с целью упрощения исследования. В логике настоящей работы нас интересуют возможности математических моделей, позволяющих описывать экономические объекты и процессы в целях их исследования, управления и прогнозирования. Такие модели принято называть экономико-математическими.
Целью настоящей работы является обоснование возможностей использования экономико-математического моделирования для формирования предметных образовательных результатов в экономическом вузе в контексте требований рынка труда.
Материалы и методы исследования
Современный этап развития рыночной экономики трактуется исследователями как экономика знаний и кардинально отличается от предыдущей стадии формирования нелинейных тенденций для экономического развития. Сегодня управление экономикой на глобальном, национальном, региональном уровнях и уровне хозяйствующих субъектов осуществляется в условиях высокой неопределенности и многозначности, что влияет на развитие процессов производства, распределения, обмена и потребления ресурсов, товаров и услуг. В этой связи невозможно оценить эффективность таких проектов и процессов без использования экономико-математических методов и моделей.
В течение многих десятилетий экономико-математическое моделирование является одним из эффективных методов для описания сложных социально-экономических объектов и процессов. Однако сегодня его роль и значение возрастают как никогда [4].
Важность экономико-математических методов для оптимизации экономических решений отмечают многие исследователи. В ряде работ подчеркивается возможность оценки и выбора оптимальных решений среди альтернативных проектов с использованием инструментов многокритериальной оптимизации, что позволяет достичь компромисса в условиях многих предпочтений [5]. При этом достаточно значимым достоинством экономико-математического моделирования является возможность расширения границ модельного эксперимента, который невозможно осуществить в рамках реальной экономической системы, с выработкой последующих рекомендаций для управления [6].
В контексте настоящей работы обратимся к вопросу о возможности использования экономико-математического моделирования для формирования практико-ориентированных образовательных результатов в ходе предметной математической подготовки студентов экономического вуза.
Анализ образовательной практики показал, что с целью использования экономико-математического моделирования в будущей профессиональной деятельности студенту сегодня требуется запас знаний в части основ математического моделирования. Это позволит продвигаться от понимания простейших моделей в экономической сфере к изучению более сложных и совершенных экономико-математических моделей [4].
Представляется, что формирование навыков математического моделирования (формализация, интерпретация, внутримодельное решение) в процессе предметной подготовки может обеспечить использование соответствующих профессионально ориентированных задач. Под профессионально ориентированной задачей будем понимать задачу практического содержания, для решения которой используют математические модели и методы. В таблице предложена структура комплекса профессионально ориентированных задач в рамках дисциплин предметной области «Математика» (табл. 1).
Анализ таблицы демонстрирует возможность организации математической подготовки с использованием приемов математического моделирования как в рамках базовых, так и вариативных учебных дисциплин.
Рассмотрим квазипрофессиональную задачу проектного типа, включенную нами в содержание дисциплины «Элементы линейной алгебры и балансовые модели в экономике».
Таблица 1
Структура комплекса профессионально ориентированных математических задач
|
№ |
Типы задач |
Примеры задач |
Дисциплины |
|
1. |
Учебно- предметные |
Задачи, использующие матрицы, векторы, системы линейных уравнений в качестве математических моделей; задачи, использующие функции полезности, прибыли, дохода, кривые безразличия, производственные функции, предельные экономические величины, коэффициент эластичности, экономический смысл интеграла |
Высшая математика |
|
Задачи, использующие вероятностные величины, выборочный метод, функцию и закон распределения случайной величины |
Теория вероятностей и математическая статистика |
||
|
Задачи, использующие элементы теории множеств, логику высказываний, основы комбинаторного анализа, графы и сети как примеры математических моделей |
Элементы дискретной математики |
||
|
2. |
Междисциплинарные |
Задачи, использующие модель спроса и предложения, задачи оптимизации налогообложения |
Высшая математика |
|
Задачи статистической оценки корреляционно-регрессионных связей |
Теория вероятностей и математическая статистика |
||
|
Задачи, использующие модели В. Леонтьева «затраты – выпуск», равновесных цен, международной торговли |
Элементы линейной алгебры и балансовые модели в экономике |
||
|
Задачи линейного программирования, динамического программирования, сетевого планирования, задачи теории игр |
Методы оптимальных решений |
||
|
Задачи начисления простых и сложных процентов, непрерывного наращения и дисконтирования |
Основы финансовых вычислений |
||
|
3. |
Квазипрофессиональные |
Задачи проектного типа для исследования балансовых соотношений в экономических системах |
Элементы линейной алгебры и балансовые модели в экономике |
|
Задачи проектного типа для оценки эффективности инвестиций и анализа финансовых рисков |
Математические основы финансовых решений |
||
|
Задачи проектного типа моделирования систем массового обслуживания |
Эконометрические исследования в экономике |
Проектное задание
Омский нефтеперерабатывающий завод, дочернее предприятие компании «Газпромнефть», является одним из самых современных нефтезаводов России и одним из крупнейших в мире. В ассортименте продукции на 2022 г. имеется газ углеводородный сжиженный для коммунально-бытового потребления и промышленных целей. С целью переработки объемов газа на 1 млн руб. нефтезавод должен использовать электроэнергии на сумму 0,25 млн руб. и обеспечить такую же сумму на транспортировку газа по магистральному газопроводу. Поставщиком электроэнергии является теплоэлектроцентраль № 4 (ТЭЦ-4) в качестве структурного подразделения Омского филиала ОАО «ТГК-11». С целью производства электроэнергии на 1 млн руб. затраты ТЭЦ-4 составляют: 0,65 млн руб. для промышленных объемов газа, 0,05 млн руб. для производства электроэнергии в рамках собственных нужд и 0,05 млн руб. для транспортных расходов на обслуживание газопровода. В свою очередь, магистральному газопроводу для транспортировки на 1 млн руб. нужно затратить газа на 0,55 млн руб. (при условии уникальной технологии) и электроэнергии на 0,1 млн руб. Известно, что в октябре 2022 г. жителям г. Омска и Омской области для коммунально-бытового потребления необходимы объем газа общей стоимостью 50 млрд руб. и электроэнергии – 25 млрд руб. Требуется найти валовый объем продукции каждой отрасли (в млрд руб.) и определить запас продуктивности структурной матрицы для оценки границ производственных возможностей сложившейся технологии.
Таблица 2
Таблица МОБ нефтехимического комплекса
|
Отрасли производства |
Отрасли потребления |
Конечная продукция Y |
Валовая продукция X |
||
|
Нефтезавод |
ТЭЦ |
Магистральный газопровод |
|||
|
Нефтезавод |
x11 |
x12 |
x13 |
50 |
x1 |
|
ТЭЦ |
x21 |
x22 |
x23 |
25 |
x2 |
|
Магистральный газопровод |
x31 |
x32 |
x33 |
0 |
x3 |
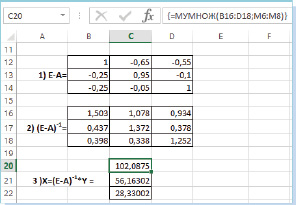
Рис. 1. Расчет вектора валовой продукции в MS Excel
Реализация проекта
Для выполнения проектного задания необходимо построить и исследовать модель многоотраслевого баланса (МОБ) В. Леонтьева. Представим данные задачи в табличной форме, рассматривая в соответствии с условием задачи стоимостной баланс (таблица МОБ нефтехимического комплекса производства газа – табл. 2).
Известны технологическая матрица А и вектор объемов конечной продукции Y
, 
.
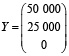Математическая модель МОБ имеет вид
.
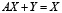Выразим вектор валовой продукции
.
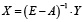Выполним расчеты, используя инструменты MS Excel (рис. 1).
Прогнозируемый вектор валовой продукции имеет вид
.
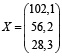Интерпретируя полученный результат, получаем: объем производимого газа составляет 102,1 млрд руб.; затраты электроэнергии 56,2 млрд руб.; транспортные расходы 28,3 млрд руб.
Выполним оценку продуктивности технологии производства газа. Для этого определим запас продуктивности технологической матрицы
.
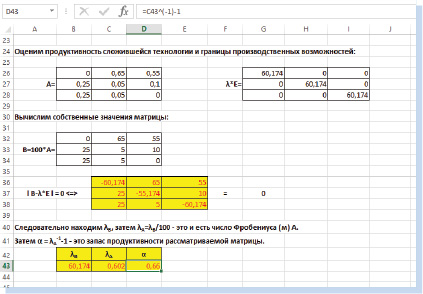
Рис. 2. Решение характеристического уравнения в MS Excel
Вычислим собственные значения матрицы В = 100А. Для этого решим характеристическое уравнение
,
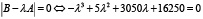имеющее три корня
.
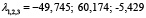Для нахождения корней характеристического уравнения целесообразно использовать инструменты MS Excel. Мы используем метод подбора параметра (рис. 2).
Число Фробениуса матрицы В равно 60,174. Тогда число Фробениуса матрицы А составляет
.
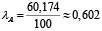Поскольку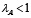 
, то технологическая матрица продуктивна.
Оценим запас продуктивности матрицы А, используя формулу
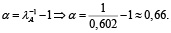
Интерпретация результатов экономико-математического моделирования
Оценка производственных возможностей технологии переработки газа демонстрирует уровень верхней границы увеличения прямых затрат в 66 %. То есть рост объемов затрат продукции i отрасли, необходимой для производства 1 ед. продукции j отрасли, не должен превышать 66 %. В противном случае технологический процесс утратит продуктивность.
Результаты исследования и их обсуждение
С целью решения проблемы повышения конкурентоспособности студентов средствами экономико-математического моделирования в процессе предметной математической подготовки нами разработан комплекс профессионально ориентированных математических задач экономического содержания. Структура комплекса включает учебно-предметные, междисциплинарные и квазипрофессиональные задачи. Учебно-предметные и междисциплинарные задачи составляют содержание базовых и вариативных математических дисциплин в рамках образовательной программы бакалавриата. В свою очередь, квазипрофессиональные задачи, как средство организации проектного обучения, могут быть использованы в содержании вариативных математических дисциплин программ бакалавриата и магистратуры, а также для организации научно-исследовательской работы будущих бакалавров и магистров.
Представляется, что использование комплекса профессионально ориентированных математических задач предоставляет возможность обращения в рамках каждой темы дисциплин предметной области «Математика» к примерам математических моделей, технологиям их построения и использования для изучения реальных процессов в сфере будущей профессиональной деятельности и творческого решения профессиональных проблем.
Заключение
Подведем итог. Актуальность вопроса формирования конкурентоспособности будущих бакалавров и магистров экономики не вызывает сомнения и требует переоценки инструментов для формирования знаний, умений и навыков в рамках предметной подготовки в высшей школе. При этом использование экономико-математического моделирования в процессе предметной математической подготовки обеспечивает практическую направленность и востребованность образовательных навыков, прежде всего, в контексте отношений «бизнес – образование – рынок труда».