Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

В контексте возрастающих требований к качеству подготовки выпускников экономических вузов особую значимость приобретает проблема интеграции учебных дисциплин. Это связано в первую очередь с компетентностным форматом образовательных результатов, обеспечивающим формирование адаптивного потенциала личности, в том числе профессиональной адаптивности в быстро изменяющемся мире [1].

В рамках образовательной практики у термина «интеграция» имеется несколько значений:

1) формирование у обучающихся целостного мнения о существующем мире (то есть в данном случае интеграция является целью обучения и реализуется на уровне знаний);

2) возможность поиска платформы сближения предметных знаний (в этом случае интеграция есть средство обучения, которое реализуется на уровне видов деятельности).

Мы разделяем мнение В.А. Далингера о том, что в решении проблемы интеграции учебных дисциплин важен выбор основ интеграции, которые будут играть системообразующую роль [2].

Учитывая вышесказанное, обратимся к вопросу интеграции математической и профессиональной подготовки будущих экономистов средствами математического моделирования.

В логике настоящего исследования представляется важным определить сущность термина «профессионально направленное обучение».

Существует несколько интерпретаций понятия профессиональной направленности в образовании. По мнению Э.Ф. Зеер, Н.В. Кузьминой, В.А. Сластенина, А.Б. Каганова, профессиональная направленность – это некая система потребностей, мотиваций, демонстрирующих, как обучающийся относится к выбранной профессии. Здесь профессиональная направленность выступает как главный мотив обучения, стимулирующий студентов к развитию познавательной активности. При изучении отдельных учебных дисциплин уровень профессиональной направленности определяется несколькими составляющими: отношением к профессии и отношением к изучаемой дисциплине. По мнению же А.Я. Кудрявцева, М.И. Махмутова, проблема профессиональной направленности раскрывается с точки зрения конструирования содержания образования в соответствии с межпредметными связями учебных дисциплин.

Придерживаясь точки зрения А.А. Вербицкого, под профессионально направленным обучением математике будем понимать конструирование содержания изучаемого материала и организацию его освоения в тех формах и видах деятельности, которые отвечают логике учебных курсов и моделируют задачи из сферы будущей профессиональной деятельности [3].

В качестве цели настоящего исследования полагаем необходимым разработать комплекс профессионально ориентированных математических задач экономического содержания, обеспечивающих формирование у студентов навыков математического моделирования реальных жизненных и профессиональных проблем в ходе математической подготовки.

Материалы и методы исследования

Рассмотрим возможности метода математического моделирования в исследовании и прогнозировании реальных процессов из сферы будущей профессиональной деятельности.

Прежде всего, обратимся к трактовке термина «модель», происходящего от латинского modulus (мера, образец, норма). Существуют различные подходы к определению понятия. Обобщение результатов анализа существующих трактовок понятия (В.А. Штофф, Л.И. Лопатников, Н.А. Орехов и др.) дает возможность говорить о том, что моделью является условный образ объекта, который концентрирует в себе наиболее важные черты и применяется для проведения исследования.

Обратимся к рассмотрению математических моделей, которые позволяют изучать экономические объекты и процессы с целью прогнозирования и управления. Данные модели принято называть экономико-математическими. В современных условиях экономико-математическое моделирование является наиболее эффективным инструментом для описания сложных социально-экономических процессов и объектов и позволяет сформировать знания о результатах изменений, не прибегая к дорогостоящим эмпирическим экспериментам [4].

В контексте вышесказанного важно конкретизировать понятие профессионально ориентированной математической задачи, дидактическая суть которой отражает ее практическое содержание, позволяющее реализовать межпредметные связи математики и экономических дисциплин и раскрывающее прикладные аспекты фундаментальных знаний в профессиональной деятельности.

В ходе проведенного исследования нами разработан комплекс профессионально ориентированных математических задач экономического содержания.

Мы разделяем мнение академика А.А. Вербицкого в части целесообразности усвоения содержания образования в результате собственной познавательной активности в рамках проектирования предметного и социального контекста будущей профессиональной деятельности. В связи с тем, что предметное содержание деятельности студентов проектируется как система учебных проблемных ситуаций и задач, отражающих профессиональные функции выпускников, а социальное содержание – благодаря выбору форм коллективной деятельности студентов, в соответствии с предложенными А.А. Вербицким базовыми формами деятельности студентов, нами выделены типы профессионально ориентированных математических задач экономического содержания: учебно-предметные, междисциплинарные, квазипрофессиональные.

Исходные данные для сетевого графика

Далее будет представлена характеристика указанных типов профессионально ориентированных задач, обеспечивающих развитие навыков математического моделирования в ходе предметной математической подготовки.

Учебно-предметные задачи включаются в учебный процесс в рамках конкретных дисциплин предметной области «Математика». Содержание задач имеет экономическую фабулу. В задачах данного типа математическая модель обычно известна, требуется выполнить внутримодельное решение и интерпретацию полученного результата.

Междисциплинарные задачи обеспечивают реализацию межпредметных связей дисциплин предметных областей «Математика», «Информатика», а также профессиональных дисциплин. Решение междисциплинарных задач требует реализации основных этапов математического моделирования. Данный тип задач выполняет пропедевтическую функцию для подготовки к решению квазипрофессиональных задач.

Представим междисциплинарную задачу, для решения которой необходимо построить сетевой график, как пример математической модели для планирования комплекса взаимосвязанных работ с известной продолжительностью технологических операций.

Задача 1. Финансовый директор нового медицинского центра составил перечень работ на начальном этапе и определил их продолжительность (таблица). Построить и упорядочить сетевой график. Найти критический путь и длину.

При выполнении задачи целесообразно использовать инструменты MS Excel. Построение и упорядочение сетевого графика позволяет студентам научиться определять, продолжительность каких работ необходимо сократить в первую очередь с тем, чтобы уменьшить время выполнения проекта.

Квазипрофессиональные задачи используются для организации проектного обучения, научно-исследовательской работы студентов, обеспечивая развитие способностей постановки проблемы, создания математической модели, ее решения и выработки по результатам исследования практических рекомендаций. Очевидна направленность задач указанного типа на формирование профессиональных компетенций студентов.

Продемонстрируем преимущества выделенных типов профессионально ориентированных математических задач в формировании навыков математического моделирования. Приведем пример квазипрофессиональной задачи, включенной нами в содержание дисциплины «Основы финансовых вычислений» [5].

Задача 2. Контекст ситуации: Финансовая компания «Сибирская Группа» владеет ценными бумагами, переоценку эффективности которых проводит ежегодно. Инвестиционный портфель компании включает два вида акций. Статистическим путем установлено, что средние доходности акций за 2021 г. составили 20 и 10 % соответственно. По результатам наблюдений с использованием MS Excel получена ковариационная матрица доходностей портфеля .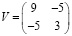

Проблема:

Подзадача 1. Найти портфель минимального риска.

Подзадача 2. Найти эффективность портфеля минимального риска.

Подзадача 3. Рассчитать минимальный риск портфеля.

Решение:

Подзадача 1. Портфель представляет совокупность инвестиционных инструментов (акций, облигаций и т.д.) для достижения инвестиционной цели.

С целью нахождения портфеля минимального риска (σ) найдем минимум целевой функции

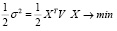
при условии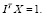

Для этого рассмотрим функцию Лагранжа:

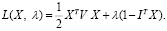
Приравнивая к нулю производные функции по Х и λ, получаем систему

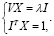
решением которой являются

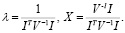
Получается, что портфель минимального риска выглядит следующим образом:

где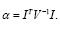

При заданном контексте кейса получаем

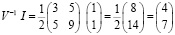
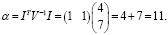
Тогда портфель минимального риска равен

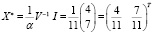
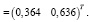
Подзадача 2. Одним из наиболее важных показателей портфеля считают его доходность, которая является случайной величиной. Эффективность портфеля (ожидаемая доходность) – это математическое ожидание доходности портфеля, состоящее из ожидаемых доходностей его ценных бумаг. Учитывая свойства математического ожидания, эффективность портфеля рассчитаем следующим образом:

,

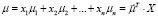где μ – эффективность портфеля;

μi – математическое ожидание доходности ценной бумаги вида i;

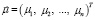– вектор ожидаемых доходностей ценных бумаг.

Эффективность портфеля минимального риска при известном векторе ожидаемых доходностей бумаг 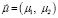, где μ1 = 0,2 и μ2 = 0,1, равна

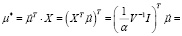
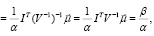
где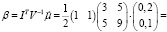

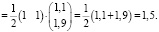
Следовательно,

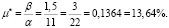
Подзадача 3. В качестве показателя риска портфеля считаем стандартное отклонение ожидаемой доходности портфеля, т.е. корень квадратный из его дисперсии, равной:

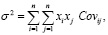
где σ – риск портфеля,

xi (xj) – доля ценной бумаги вида i (j) в портфеле;

Covij – ковариация доходностей i-го и j-го активов (мера взаимодействия, рассматривающая дисперсию индивидуальных значений доходности ценных бумаг и силу связи между изменениями их доходностей).

В финансовой практике используем матричную форму записи риска

,

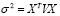где 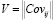– ковариационная матрица доходностей активов.

Риск портфеля составляет

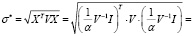
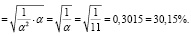
Важно, что ковариационная матрица доходностей ценных бумаг невырожденная. На практике это выполняется для рисковых активов.

Ответ: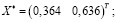

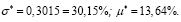
Интерпретация: Оптимальный портфель должен содержать 36,4 % и 63,6 % акций 1-го и 2-го типов соответственно. При этом минимальный риск составляет 0,3015, а ожидаемая доходность портфеля – 13,64 %. Ввиду того, что диагональные элементы ковариационной матрицы равны дисперсиям ценных бумаг, 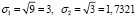, то риск портфеля оказался меньше индивидуальных рисков ценных бумаг. Это обусловлено, во-первых, низкой корреляцией ценных бумаг, а во-вторых, тем, что было определено, что доля второй бумаги в портфеле минимального риска больше доли первой практически в два раза, вместе с тем, что риск второй бумаги ниже, чем риск первой.

Обобщая функциональные возможности представленных задач в формировании приемов анализа, синтеза, а также способности формализовать исходные данные и интерпретировать полученные результаты как основные составляющие умения моделировать, выделим их наиболее сильные стороны в контексте проблемы исследования:

− профессиональная направленность;

− повышение мотивационной направленности;

− интеграция внутрипредметных и междисциплинарных знаний;

− направленность на формирование математической компетентности как составляющей профессиональной компетентности.

Результаты исследования и их обсуждение

Использование разработанного нами комплекса профессионально ориентированных математических задач обеспечивает решение проблемы профессиональной направленности предметной подготовки с позиций конструирования содержания образования на основе реализации межпредметных связей учебных дисциплин. При этом интегративная структура математической компетентности как результата математической подготовки в условиях профессионально направленного обучения обеспечивает междисциплинарность формируемых знаний, умений и навыков. Это, в свою очередь, позволяет реализовать интегративный потенциал математической подготовки в системе высшего образования.

Заключение

Подводя итог, важно отметить, что обогащение содержания предметного образования за счет использования в качестве интегративных средств обучения математических моделей, позволяющих прогнозировать реальные процессы из сферы будущей профессиональной деятельности, способствует формированию у студентов способности определять стратегии профессионального поведения и осуществлять поиск необходимого согласованного решения. В свою очередь, реализация интегративных возможностей учебных дисциплин обеспечивает повышение конкурентоспособности выпускников экономических университетов в изменяющихся социально-экономических условиях.