В условиях современной рыночной экономики и динамических перемен на рынках своевременное определение направлений развития производства, совершенствования продукции, закупки ресурсов является главным фактором успеха. Необходимы инструменты, которые позволят учитывать всё большее и большее число различных переменных, факторов, протекающих процессов, взаимосвязей между различными данными при формировании стратегий экономического развития. В связи с этим представляется весьма актуальным использование графических инструментов моделирования для определения стратегий и их последующей реализации.
Сетевые модели давно нашли широкое применение в экономике. Самыми распространёнными среди них были сетевые графики, которые часто использовались для синхронизации процедур по времени и для определения последовательности различных операций. По мере перехода к исследованию больших данных в условиях развития цифровой экономики графические технологии получают особую актуальность и дальнейшее развитие. Графическими инструментами, способными моделировать различные переменные во взаимосвязи друг с другом и для достижения общей цели, являются графы. Эффективность графов обусловлена тем, что они позволяют решать очень большой спектр задач. Среди них и информационный спектр задач (представление больших объёмов информации в сжатом виде), и решение структурных задач (структурные графы структурируют элементы любого множества), и динамические задачи (динамические графы позволяют представить любой процесс в развитии и моделировать различные варианты решения). По мере развития компьютерных технологий графы всё больше и больше используются для управления большими потоками данных. Графы основаны на сетевых моделях, но углубляют и развивают их механизм, являются более эффективными инструментами и для временной, и для затратной оптимизации процессов. Граф, в отличие от сетевых графиков, всё время хранится в паре векторов, т.е. он способен задавать направление, что очень важно при динамическом исследовании данных.
Выработка экономических стратегий всегда связана с исследованием больших потоков данных, с необходимостью их структуризации, динамического анализа их изменений, установления взаимосвязей как между отдельными видами данных, так и между потоками данных. Поэтому представляется, что использование графов для определения экономических стратегий развития является очень перспективным и актуальным направлением исследований.
Целью исследования является разработка теоретико-методологических основ моделирования продуктово-рыночных стратегий как динамической системы, включающей множество переменных данных (элементов) и взаимосвязей между ними, на основе использования динамических графов.
В процессе моделирования стратегий использовались следующие методы:
1) метод приоритетов, который заключается в том, что народнохозяйственные задачи по лучшему удовлетворению потребностей и благосостояния потребителей являются приоритетными целями по отношению ко всем другим целям при формировании любой экономической стратегии;
2) метод сквозной системности, который позволяет любую продуктовую стратегию предприятия моделировать в системе стратегического развития как самого предприятия, так и во взаимосвязи со стратегическими планами развития той отрасли промышленности, к которой предприятие относится, и стратегическими планами развития региона, на территории которого это предприятие расположено, т.е. любая стратегия должна вписываться в систему других стратегий, а также формироваться во взаимосвязи со стратегиями ресурсного обеспечения предприятия;
3) метод динамичности, который позволяет моделировать не статичное множество данных, а всегда процесс, например процесс формирования стратегии и процесс её исполнения;
4) метод адресности используется для придания стратегии ориентированности, например, формирование стратегий по видам продукции, стратегий ассортиментного предложения на определённом рынке, стратегий использования различного вида ресурсов, стратегий по ресурсному обеспечению в целом производства или производства определённого вида продукта, другие адресные стратегии развития;
5) метод комплексного подхода позволяет при определении стратегии учитывать весь комплекс различных факторов на динамику данных, условий хозяйствования, целей развития;
6) методы анализа и синтеза необходимы при моделировании различных стратегий, так как любая стратегия, с одной стороны, является продуктом анализа, поскольку основана на исследовании детализированных данных по множеству параметров, влияния на них различных факторов, процессов, но, с другой стороны, всегда является продуктом синтеза, так как направления развития определяются в результате синтеза множества данных в единое целое, способное обеспечить синергетический результат.
Все вышеперечисленные методы в полной мере являются не только методами, используемыми при моделировании стратегий, но и методами построения графов. Это особенно наглядно прослеживается на примере использования метода единства анализа и синтеза при построении графов. Любой граф состоит из элементов, множество данных которых задаются в результате комплексного и системного анализа, но суть графа при моделировании стратегии состоит в том, что он всегда представляет собой синтез множества различных элементов.
Что же такое граф? Почему он может стать эффективным графическим инструментом моделирования стратегий?
В результате проведённого исследования были выработаны теоретико-методологические основы моделирования экономических стратегий на основе использования графов.
Исходя из авторского определения стратегии как продукта синтеза множества различных данных, полученного в результате анализа [1], а также стратегии как динамической системы, включающей множество различных подсистем, их элементов и взаимосвязей между ними, следует подойти и к определению моделей и моделированию экономических стратегий.
«Моделирование – исследование каких-либо явлений, процессов или систем путем построения и изучения их моделей; использование моделей для определения поведения и характеристик реальных систем» [2].
В экономической теории даётся широкое толкование разновидностей экономико-математических моделей.
«Экономико-математическая модель – математическое описание экономического процесса или объекта, произведенное в целях их исследования и управления ими» [3]. Остановимся на наиболее распространённых экономико-математических моделях.
«Модель конкуренции – модель состояния экономической системы в условиях рыночной конкуренции, отражающая соотношение между спросом, предложением и ценами на товары.
Модель Леонтьева – принятое в литературе название модели межотраслевого баланса производства и распределения продукции и услуг.
Модель общего равновесия Вальраса – модель предложения и состояния общего равновесия, описывающая все взаимосвязи рынка с помощью уравнений.
Модель Неймана – модель, предназначенная для нахождения максимально возможного темпа роста экономической системы, а также пропорций и цен, соответствующих этому темпу.
Матричная модель – экономико-математическая модель, отображающая наиболее специфические количественные и качественные характеристики исследуемых экономических процессов и явлений. Зависимости в этой модели представлены в виде упорядоченных таблиц, состоящих из m строк и n столбцов чисел. Кроме того, матричные модели могут быть представлены также в виде уравнений (линейных и нелинейных). Матричные модели применяют для анализа и планирования производства и распределения продукции на разных уровнях – от отдельных предприятий до народного хозяйства в целом.
Модель Портера – Лоулера – ситуационная теория мотивации, объединяющая элементы теории ожиданий и теории справедливости. Она включает пять переменных величин: усилие, ожидание, результативность, вознаграждение и удовлетворение.
Модель принятия решений Врума – Йеттона – вероятностная модель руководства, делающая упор на процессе принятия решений и определяющая пять типов руководства, образующих непрерывный континуум: от автократического до демократического.
Модель роста Солоу – неоклассическая модель экономического роста, в которой формулируется разностное уравнение, задающее равновесную траекторию роста при полной занятости. Модель позволяет оценить темп прироста занятости, при котором достигается устойчивое равновесие.
Модель спроса и потребления (конструктивная) – экономико-математическая модель, используемая в планировании и прогнозировании спроса и потребления. В основе этой модели лежат уравнения бюджета потребителей (уравнения, выражающие равенство объема потребления и суммы произведений количества каждого товара на его цену). Модели бюджетов потребителей играют важную роль в планировании потребления. Модель, определяющая прожиточный минимум, – одна из таких моделей.
Модель спроса и предложения (аналитическая) – экономико-математическая модель, которая строится в виде уравнений, характеризующих зависимость потребления благ (то есть товаров и услуг) от тех или иных факторов. Эта модель используется в практике планирования и прогнозирования спроса и потребления наряду с конструктивными и структурными (балансовыми) моделями» [2, 4].
Кроме того, существуют народнохозяйственная модель для сбалансированного развития отраслей народного хозяйства как единого целого, макроэкономическая модель, основанная на выбранных макроэкономических индикаторах оптимизации, микроэкономическая модель для регулирования отдельного процесса или хозяйствующего субъекта.
Несмотря на обилие экономико-математических моделей для регулирования, оптимизации и сбалансированности отдельных процессов или хозяйствующих объектов, до сих пор не создано модели формирования продуктово-рыночной или любой другой экономической стратегии. Это объясняется тем, что до настоящего времени в экономической теории преобладала точка зрения, что стратегия является абстрактной категорией, которую можно определять приблизительно и абстрактно. Однако стратегическое планирование в условиях рыночной экономики основано именно на выборе стратегий развития на долгосрочную перспективу, что обусловливает важность верного и точного выбора экономических стратегий. Теория стратегий с каждым годом развивается, база различных стратегий и подстратегий становится всё шире и шире. Мировая практика идёт по пути развития программных продуктов, раскрывающих большие возможности для использования современных методов спектрального и векторного анализа, в том числе для наиболее сбалансированного и верного выбора оптимальных стратегий развития предложения продукции. Представляется, что векторный анализ, в основе которого лежит выбор вектора или векторов развития, и моделирование стратегий имеют единую сущность, так как выбор стратегии, по сути, и означает выбор вектора (направления) развития. В ходе исследования был выработан принципиально новый теоретико-методологический подход к моделированию стратегий на основе векторного анализа как такового и теории графов в частности. Что же такое модель стратегии? В ходе исследования было сформулировано следующее определение. Модель стратегии – это векторная модель, позволяющая определить оптимальную стратегию путём отыскания в единой системе координат времени и пространства сонаправленных и наиболее согласованных друг с другом векторов условий, возможностей и искомой стратегии развития, либо такие векторы решений, путь которых приводит к искомой вершине – оптимальному вектору развития. Векторные модели сродни любой математической модели. «Математическая модель – система математических соотношений, описывающих изучаемый процесс или явление на основе, например, теории множеств, теории графов, теории вероятности…» [2].
Какие же из математических моделей наиболее близки к векторной модели формирования стратегий? Особого внимания заслуживают адаптивная, имитационная и динамическая модели. Адаптивная модель сродни ситуационной модели, она составляется, как правило, на текущий период, в её основе лежат данные прогноза временной последовательности, и она способна отражать изменение временного ряда с учётом изменяющихся условий.
Имитационная модель основана на взаимосвязях между элементами системы и отображает зависимости выходов системы от её входов, эта модель часто используется в теории управления для воспроизводства и оценки системы во времени.
Динамическая модель в отличие от статической модели устанавливает зависимости моделируемых переменных текущего периода от экзогенных и эндогенных переменных предшествующего периода и фактически моделирует развитие процесса в будущем времени. Все эти модели имеют схожие черты, так как предназначены для моделирования исследуемого объекта во времени.
Векторная модель сочетает в себе элементы и динамической, и адаптивной, и имитационной математических моделей, так как векторная модель предназначена для моделирования значений элементов векторов текущего состояния с учётом предшествующих значений и развития условий хозяйствования, что сродни динамической модели, но для прогноза в долгосрочном периоде стратегических векторов развития, что сродни адаптационной модели, а также внутри векторной модели устанавливаются взаимосвязи между векторами или их сонаправленность, без чего векторная модель просто не будет работать, что сродни имитационной модели. Наиболее распространёнными должны стать векторные модели, моделирующие состояние системы векторов в многомерной системе координат, в том числе прогнозирование данных элементов векторов в единой системе координат времени и пространства [1]. Однако не меньшую актуальность и значимость имеют и векторные модели в виде графов. В этой статье более подробно остановимся на моделировании стратегий с помощью графов.
Граф в переводе с греческого – пишу, описываю. Любое отношение можно описать с помощью графа. В теории граф определяется как «математическая абстракция реальной системы объектов любой природы, обладающих парными связями». «Граф как математический объект есть совокупность двух множеств – множества самих объектов, называемого множеством вершин, и множества парных связей, называемого множеством рёбер. Элемент множества рёбер есть пара элементов множества вершин» [5]. В большом экономическом словаре граф определяется как «непустое конечное множество узлов, а также рёбер, соединяющих пары различных вершин» [2]. В теории различают графы ориентированные и неориентированные. «Если каждому ребру приписано направление, то граф называется ориентированным, или орграфом. Граф обычно представляют в наглядной форме, изображая вершины точками, а ребра – линиям» [6].
Таким образом, опираясь на теоретические исследования [6–8], автор считает, что граф – это не просто описание, а граф – это модель, потому что граф, как и каждая модель, состоит из множества элементов (в данном случае – вершин) и множества их взаимосвязей (в данном случае – рёбер).
Учитывая авторское определение стратегии как синтезированной системы, представляющей из себя множество, внутри которого устанавливаются взаимосвязи между её неотъемлемыми элементами, которые только все вместе формируют направление стратегии и определяют её результативность, можно сделать вывод, что использование графов является очень органичным и эффективным инструментом моделирования стратегий. Учитывая, что стратегия – это всегда направление, вектор развития, то для моделирования стратегий наиболее подходит ориентированный граф. Итак, любой граф – это множество, которое обозначают G, состоящее из множества вершин, обозначаемых V, и множества рёбер, обозначаемых Е. Ребро называется дугой, если оно имеет направление. Поэтому в формируемых графах для моделирования стратегий все рёбра будут являться дугами. Ориентированный граф – совокупность двух множеств непустого множества V и множества Е дуг или упорядоченных пар различных элементов множества V. Множество вершин (V) и множество дуг (Е) включают свои элементы, соответственно: вершины, обозначаемые v1, v2, … vn и дуги, обозначаемые e1, e2, … em. Тогда соседние (смежные) вершины, обозначаемые v1, v2, которые обе являются концами одной дуги e1, с одной стороны, являются элементами множества вершин V, а с другой стороны, формируют ребро e1, являющееся элементом множества Е. Эти взаимосвязи и множества графа можно записать следующим образом:
G (V, E) = (V, E), V ≠ ∅, (1)
где v1 ∈ V(G), v2 ∈ V(G), (2,3)
e1 = {v1, v2}, e1 ∈ E(G), (4,5)
({v1, v2} ¬ <) ∈ E(G). (6)
Если речь идёт о формировании стратегии или её реализации, то чаще всего моделируется процесс, который и есть путь графа. «Путь графа – это последовательность вершин, в которой каждая вершина соединена со следующей ребром. Длина пути – это число рёбер, используемых в пути, при этом многократно используемые рёбра считаются соответствующее число раз [6]. Ориентированным маршрутом или путём в орграфе называют конечную последовательность вершин и дуг, в которой каждый элемент инцидентен предыдущему и последующему» [5, 6]. Процесс формирования товарной стратегии можно представить в виде динамического циклического графа, рёбра которого задают время осуществления операций (рис. 1).
Условные обозначения к рис. 1:
G1 – орграф, представленный на рис. 1; V – множество вершин; Е – множество дуг;
v1 – вершина, характеризующая событие по проведению анализа конкурентоспособности продукта при входе в процесс (т.е. анализа конкурентоспособности базовых поколений данного типа продукта при прежних товарных стратегиях) и при выходе из процесса (т.е. анализа конкурентоспособности сформированной долгосрочной товарной стратегии);
e1 = {v1, v2} – дуга, характеризующая путь (работу) от события v1 к событию v2;
v2 – вершина, характеризующая событие по анализу делового окружения фирмы и на базе этого по определению подстратегии по покупателям и потребительским сегментам позиционирования на рынках продуктов формулируемой товарной стратегии;
e2 = {v2, v3} – дуга, характеризующая путь (работу) от события v2 к событию v3;
v3 – вершина, характеризующая событие по анализу рынков, потребительского спроса и на базе этого по определению подстратегии ассортиментного предложения формируемой товарной стратегии;
e3 = {v3, v4} – дуга, характеризующая путь (работу) от события v3 к событию v4;
v4 – вершина, характеризующая событие по анализу жизненных циклов продукции и на базе этого по определению подстратегии жизненных циклов производства и предложения продуктов формируемой товарной стратегии;
e4 = {v4, v5} – дуга, характеризующая путь (работу) от события v4 к событию v5;
v5 – вершина, характеризующая событие по анализу НТП, тенденций развития продуктового ряда, резервов усовершенствования продуктов и на базе этого по определению подстратегии качества продуктов формируемой товарной стратегии;
e5 = {v5, v6} – дуга, характеризующая путь (работу) от события v5 к событию v6;
v6 – вершина, характеризующая событие по анализу технико-технологической базы производства, загруженности производственных мощностей, изменения масштабов производства и на основе этого по определению подстратегии масштабов (объёма) производства продуктов формируемой товарной стратегии;
e6 = {v6, v7} – дуга, характеризующая путь (работу) от события v6 к событию v7;
v7 – вершина, характеризующая событие по анализу рациональности конструкции и материально-вещественного состава продуктов и на базе этого по определению подстратегии ценового диапазона предложения продуктов формируемой товарной стратегии;
e7 = {v7, v8} – дуга, характеризующая путь (работу) от события v7 к событию v8;
v8 – вершина, характеризующая событие по анализу технико-технологических резервов интенсивности производства, оптимальности затрат на изготовление продуктов и на базе этого по определению подстратегии экономии издержек производства для формируемой товарной стратегии;
e8 = {v8, v9} – дуга, характеризующая путь (работу) от события v8 к событию v9;
v9 – вершина, характеризующая событие по анализу эффективности рекламы и оптимальности затрат на сбыт продукции и на базе этого по определению сбытовой подстратегии формируемой товарной стратегии;
e9 = {v9, v10} – дуга, характеризующая путь (работу) от события v9 к событию v10;
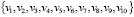– элементы (вершины) множества V;
v10 – вершина, характеризующая событие по синтезу товарной стратегии;
e10 = {v10, v1} – дуга, характеризующая путь (работу) от события v10 к событию v1 для оценки конкурентоспособности сформированной товарной стратегии и при необходимости её корректировки, когда весь цикл начинается заново.
Граф, построенный на рис. 1, является связанным, т.е. из одной его вершины в другую есть путь в виде ребра, он является ориентированным, так как все пути этого графа ориентированные, они имеют направление. Граф является полным, т.е. любые его две вершины соединены дугой. Построенный граф является пленарным, так как его можно изобразить на плоскости без пересечения рёбер (дуг). Кроме того, данный граф следует формировать как взвешенный, так как для каждого ребра графа можно определить число, называемое весом ребра. Это число чаще всего должно отражать временную продолжительность, но может отражать и стоимость прохождения пути, т.е. время или стоимость проведения конкретного анализа для формирования определённой подстратегии формируемой товарной стратегии предприятия. Тем самым рис. 1 иллюстрирует пример графа, который позволяет смоделировать время, необходимое для осуществления анализа и формирования определённой подстратегии, т.е. данные дуг для достижения каждой из вершин. Аналогичным образом подобный граф позволяет смоделировать и стоимость для каждого события (вершины) общего цикла. Это очень важно для рационализации и оптимизации процесса формирования товарной стратегии. Любая товарная стратегия является продуктово-рыночной стратегией, так как она определяет не только процесс и стадии изготовления продукции, т.е. процесс формирования продуктовой стратегии, но и процесс формирования рыночной стратегии для позиционирования продукции на рынке.
Построенный пример графа характеризует не только процесс, но и цикл. Циклом называют цепь, в которой первая и последняя вершина совпадают. Граф содержит 10 вершин, из вершины 10 лежит путь в вершину 1. При входе в цикл графа процесс начинается с анализа конкурентоспособности прежней товарной стратегии, а после синтеза новой товарной стратегии и при выходе из цикла графа анализируют конкурентоспособность сформированной товарной стратегии, возвращаясь в вершину 1, т.е. показан цикл корректировки или смены товарной стратегии. Построенный пример графа можно записать следующим образом.
G1(V, E) = (V, E), V≠∅ (1)
v1 ∈ V(G1), v2 ∈ V(G1), v3 ∈ V(G1), v4 ∈ V(G1),
v5 ∈ V(G1), v6 ∈ V(G1), v7 ∈ V(G1), v8 ∈ V(G1),
v9 ∈ V(G1), v10 ∈ V(G1), (2–12)
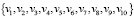∈ V(G1), (13)
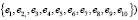∈ E(G1), (14)
e1 = {v1, v2}, e2 = {v2, v3}, e3 = {v3, v4}, e4 = {v4, v5},
e5 = {v5, v6}, e6 = {v6, v7}, e7 = {v7, v8}, e8 = {v8, v9},
e9 = {v9, v10}, e10 = {v10, v1}, (15–24)
(
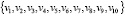¬ <) ∈ E(G1) (25)
С помощью аналогичного графа можно смоделировать и каждую из подстратегий товарной стратегии, но наиболее актуальным является построение графа для моделирования стратегии комплексного жизненного цикла продукта как товара (рис. 2).
Условные обозначения к рис. 2:
G2 – орграф, представленный на рис. 2; V – множество вершин; Е – множество дуг;
v1 – вершина, характеризующая событие по процессу проведения НИР для разработки нового продукта;
e1 = {v1, v2} – дуга, характеризующая продолжительность пути от события v1 к событию v2, т.е. продолжительность стадии НИР продукта;
v2 – вершина, характеризующая событие по процессу проведения ОКР продукта;
e2 = {v2, v3} – дуга, характеризующая продолжительность пути от события v2 к событию v3, т.е. продолжительность стадии ОКР продукта;
v3 – вершина, характеризующая событие по процессу технической подготовки производства (ТПП) для последующего производства продукта;
e3 = {v3, v4} – дуга, характеризующая продолжительность пути от события v3 к событию v4, т.е. продолжительность стадии ТПП продукта;
v4 – вершина, характеризующая событие по организационной подготовке производства (ОПП) для последующего производства продукта;
e4 = {v4, v5} – дуга, характеризующая продолжительность пути от события v4 к событию v4, т.е. продолжительность стадии ОПП продукта;
v5 – вершина, характеризующая событие по процессу производства продукта;
e5 = {v5, v6} – дуга, характеризующая продолжительность пути от события v5 к событию v6, т.е. продолжительность стадии производства продукта;
v6 – вершина, характеризующая событие по процессу внедрения товара на рынок в период зарождения спроса на него;
e6 = {v6, v7} – дуга, характеризующая продолжительность пути от события v6 к событию v7, т.е. продолжительность стадии внедрения товара на рынок;
v7 – вершина, характеризующая событие по процессу роста продаж товара в период ускорения и роста спроса на него;
e7 = {v7, v8} – дуга, характеризующая продолжительность пути от события v7 к событию v8, т.е. продолжительность стадии роста предложения товара;
v8 – вершина, характеризующая событие по процессу стабильного предложения товара в период зрелого спроса на товар;
e8 = {v8, v9} – дуга, характеризующая продолжительность пути от события v8 к событию v9 , т.е. продолжительность стадии стабильного предложения товара;
v9 – вершина, характеризующая событие по процессу снижения предложения товара на стадии снижения спроса на него;
e9 = {v9, v10} – дуга, характеризующая продолжительность пути от события v9 к событию v10, т.е. продолжительность стадии снижения предложения товара;
v10 – вершина, характеризующая событие по процессу снятия товара с производства и ухода его с рынка при критическом снижении и исчезновении спроса на него;
e10 = {v10, v1} – дуга, характеризующая продолжительность пути от события v10 к событию v1, т.е. стадии снятия товара с производства до стадии научно-исследовательских разработок нового продукта (товара).
Исходя из условных обозначений орграфа, представленного на рис. 2, в сокращённом виде его можно описать с помощью следующих математических формул:
G2(V, E) = (V, E), V≠∅ (1)
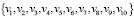∈ V(G2), (2)
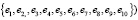∈ E(G2), (3)
(
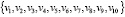¬ <) ∈ E(G2) (4)
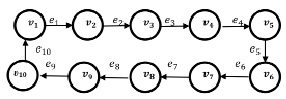
Рис. 1. Граф (G1 ) моделирования товарной стратегии
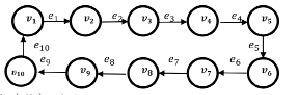
Рис. 2. Граф (G2 ) моделирования стратегии жизненного цикла продукта как товара
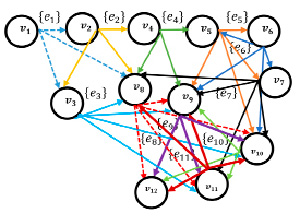
Рис. 3. Граф (G3 ) моделирования ресурсной стратегии на примере технико-технологической стратегии обеспечения производства
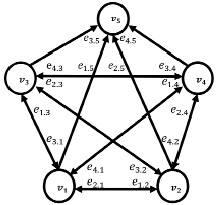
Рис. 4. Граф (G4 ) моделирования стратегии как системы
Таким образом, построенный граф (рис. 2) точно так же характеризует цикл, является ориентированным, пленарным, связанным и полным. Все его дуги взвешены по времени продолжительности стадий изготовления и стадий сбыта товара. Рассмотренный пример графа является незаменимым инструментом для моделирования и планирования стратегий по продолжительности стадий жизненного цикла товара с учётом влияния продолжительности стадий друг на друга (конец предыдущей является началом следующей) и в зависимости от стадий жизненного цикла спроса, что позволяет значительно повысить конкурентоспособность продукции.
Рассмотренные примеры характеризуют простую цепь графа, так как в его маршруте нет повторяющихся дуг и повторяющихся вершин, но на практике может потребоваться большая детализация событий (вершин) и возникнуть более сложные связи между ними, а следовательно, потребуется создавать более сложные цепочки графа. Это прослеживается на примере процесса моделирования ресурсных стратегий, связанных с определённой товарной стратегией. Они точно так же, как и стратегии жизненного цикла продукта, связаны с работой функциональных служб предприятия, так как от используемых ресурсов зависит их производительность, а также со службами маркетинга и материально-технического снабжения (МТС). Рассмотрим наиболее типичный тип графа на примере формирования технико-технологической ресурсной стратегии для осуществления товарной стратегии. При построении графа учитывалось, что любая ресурсная стратегия закупок ресурсов находится в прямой зависимости от продуктовой программы. Поэтому стратегии по ассортименту, качеству, цене, объёму закупаемых ресурсов моделировались в зависимости от стратегий по объёму и издержкам производства и качества продукции.
Условные обозначения к рис. 3:
G3 – орграф, представленный на рис. 3; V – множество вершин; Е – множество дуг;
v1 – вершина, характеризующая событие по процессу анализа существующей материально-технической базы (например, средств труда, технологий) и уровня загруженности производственных мощностей;
e1.2 = {v1, v2} – дуга, характеризующая путь от события v1 к событию v2;
e1.3 = {v1, v3} – дуга, характеризующая путь от события v1 к событию v3;
e1.8 = {v1, v8} – дуга, характеризующая путь от события v1 к событию v8;
{e1} ∈ {e1.2, e1.3, e1.8} – множество дуг, которые выходят из вершины v1 (на рис. 3 пучок векторов {e1} обозначен голубыми штрихпунктирными линиями);
v2 – вершина, характеризующая событие по процессу анализа товарной стратегии по объёму производства продукции;
e2.3 = {v2, v3} – дуга, характеризующая путь от события v2 к событию v3;
e2.4 = {v2, v4} – дуга, характеризующая путь от события v2 к событию v4;
e2.8 = {v2, v8} – дуга, характеризующая путь от события v2 к событию v8;
{e2} ∈ {e2.3, e2.4, e2.8} – множество дуг, которые выходят из вершины v2 (на рис. 3 пучок векторов {e2}обозначен жёлтыми линиями);
v3 – вершина, характеризующая событие по процессу анализа рынков технологий и средств труда;
e3.8 = {v3, v8} – дуга, характеризующая путь от события v3 к событию v8;
e3.9 = {v3, v9} – дуга, характеризующая путь от события v3 к событию v9;
e3.10 = {v3, v10} – дуга, характеризующая путь от события v3 к событию v10;
e3.11 = {v3, v11} – дуга, характеризующая путь от события v3 к событию v11;
{e3} ∈ {e3.8, e3.9, e3.10, e3.11} – множество дуг, которые выходят из вершины v3 (на рис. 3 пучок векторов {e3} обозначен бирюзовыми линиями);
v4 – вершина, характеризующая событие по анализу товарной стратегии по предельным издержкам производства;
e4.5 = {v4, v5} – дуга, характеризующая путь от события v4 к событию v5;
e4.8 = {v4, v8} – дуга, характеризующая путь от события v4 к событию v8;
e4.9 = {v4, v9} – дуга, характеризующая путь от события v4 к событию v9;
{e4} ∈ {e4.5, e4.8, e4.9} – множество дуг, которые выходят из вершины v4 (на рис. 3 пучок векторов {e4} обозначен зелёными линиями);
v5 – вершина, характеризующая событие по процессу анализа товарной стратегии по позиционированию продукции на рынках и ценовому диапазону её продаж;
e5.6 = {v5, v6} – дуга, характеризующая путь от события v5 к событию v6 ;
e5.7 = {v5, v7} – дуга, характеризующая путь от события v5 к событию v7;
e5.9 = {v5, v9} – дуга, характеризующая путь от события v5 к событию v9;
e5.10 = {v5, v10} – дуга, характеризующая путь от события v5 к событию v10;
{e5} ∈ {e5.6, e5.7, e5.9, e5.10} – множество дуг, которые выходят из вершины v5 (на рис. 3 пучок векторов {e5} обозначен оранжевыми линиями);
v6 – вершина, характеризующая событие по процессу анализа товарной стратегии по качеству продукции;
e6.5 = {v6, v5} – дуга, характеризующая путь от события v6 к событию v5;
e6.7 = {v6, v7} – дуга, характеризующая путь от события v6 к событию v7;
e6.9 = {v6, v9} – дуга, характеризующая путь от события v6 к событию v9;
e6.10 = {v6, v10} – дуга, характеризующая путь от события v6 к событию v10;
{e6} ∈ {e6.5, e6.7, e6.9, e6.10} – множество дуг, которые выходят из вершины v6 (на рис. 3 пучок векторов {e6} обозначен синими линиями);
v7 – вершина, характеризующая событие по процессу анализа товарной стратегии по жизненному циклу продукции, включающего жизненный цикл создания и жизненный цикл предложения продукции на рынках;
e7.8 = {v7, v8} – дуга, характеризующая путь от события v7 к событию v8;
e7.9 = {v7, v9} – дуга, характеризующая путь от события v7 к событию v9;
e7.10 = {v7, v10} – дуга, характеризующая путь от события v7 к событию v10;
e7.11 = {v7, v11} – дуга, характеризующая путь от события v7 к событию v11;
{e7} ∈ {e7.8, e7.9, e7.10, e7.11} – множество дуг, которые выходят из вершины v7 (на рис. 3 пучок векторов {e7} обозначен чёрными линиями);
v8 – вершина, характеризующая событие по процессу синтеза ресурсной стратегии по ассортименту (назначению) и объёму закупок ресурса (технологий, средств труда);
e8.9 = {v8, v9} – дуга, характеризующая путь (работу) от события v8 к событию v9;
e8.10 = {v8, v10} – дуга, характеризующая путь (работу) от события v8 к событию v10;
e8.11 = {v8, v11} – дуга, характеризующая путь (работу) от события v8 к событию v11;
e8.12 = {v8, v12} – дуга, характеризующая путь (работу) от события v8 к событию v12;
{e8} ∈ {e8.9, e8.10, e8.11, e8.12} – множество дуг, которые выходят из вершины v8 (на рис. 3 пучок векторов {e8} обозначен красными штрихпунктирными линиями);
v9 – вершина, характеризующая событие по процессу синтеза ресурсной стратегии по ценовому диапазону закупаемых ресурсов (технологий и средств труда);
e9.10 = {v9, v10} – дуга, характеризующая путь от события v9 к событию v10;
e9.11 = {v9, v11} – дуга, характеризующая путь от события v9 к событию v11;
e9.12 = {v9, v12} – дуга, характеризующая путь от события v9 к событию v12;
{e9} ∈ {e9.10, e9.11, e9.12} – множество дуг, которые выходят из вершины v9 (на рис. 3 пучок векторов {e9} обозначен фиолетовыми линиями);
v10 – вершина, характеризующая событие по процессу синтеза ресурсной стратегии по качеству закупаемых ресурсов (технологий и средств труда);
e10.9 = {v10, v9} – дуга, характеризующая путь от события v10 к событию v9;
e10.11 = {v10, v11} – дуга, характеризующая путь от события v10 к событию v11;
e10.12 = {v10, v12} – дуга, характеризующая путь от события v10 к событию v12;
{e10} ∈ {e10.9, e10.11, e10.12} – множество дуг, которые выходят из вершины v10 (на рис. 3 пучок векторов {e10} обозначен светло-зелёными линиями);
v11 – вершина, характеризующая событие в результате процесса синтеза временных параметров ресурсной стратегии обеспечения производства технологическими ресурсами с учётом жизненных циклов их использования;
e11.8 = {v11, v8} – дуга, характеризующая путь от события v11 к событию v8;
e11.9 = {v11, v9} – дуга, характеризующая путь от события v11 к событию v9;
e11.10 = {v11, v10} – дуга, характеризующая путь от события v11 к событию v10;
e11.12 = {v11, v12} – дуга, характеризующая путь от события v11 к событию v12;
{e11} ∈ {e11.8, e11.9, e11.10, e11.12} – множество дуг, которые выходят из вершины v11 (на рис. 3 пучок векторов {e11} обозначен бордовыми линиями);
v12 – вершина, характеризующая конечное событие по процессу синтеза ресурсной стратегии закупок и использования технологии и средств труда.
Таким образом, орграф, построенный на рис. 3, можно в сокращённом виде описать с помощью математических символов следующим образом:
G3 (V, E) = (V, E), V≠∅ (1)
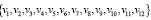∈ V(G3), (2)
{e1} ∈ {e1.2, e1.3, e1.8}; {e2} ∈ {e2.3, e2.4, e2.8};
{e3} ∈ {e3.8, e3.9, e3.10, e3.11}; {e4} ∈ {e4.5, e4.8, e4.9};
{e5} ∈ {e5.6, e5.7, e5.9, e5.10}; {e6} ∈ {e6.5, e6.7, e6.9, e6.10};
{e7} ∈ {e7.8, e7.9, e7.10, e7.11}; {e8} ∈ {e8.9, e8.10, e8.11, e8.12};
{e9} ∈ {e9.10, e9.11, e9.12}; {e10} ∈ {e10.9, e10.11, e10.12};
{e11} ∈ {e11.8, e11.9, e11.10, e11.12}; (3–13)
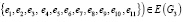(14)
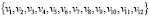¬ <) ∈ E(G3)
Построенный на рис. 3 граф является связанным, ориентированным. Он точно так же, как и графы на рис. 1, 2, изображает динамическую модель, так как с изменением значения одной переменной изменяется весь процесс. Однако этот граф уже не является циклическим, он характеризует не только последовательность и временную зависимость событий, но и воздействие одних элементов графа на другие. Поэтому из одной и той же вершины выходит не одна, а несколько дуг, входящих в разные события, на которые это событие влияет. Поэтому каждая дуга будет иметь разный вес в зависимости от того, из какого элемента (вершины) дуга выходит и в какую вершину (событие) она входит. Веса могут быть установлены в относительном выражении или с помощью балльных оценок. Такое назначение графа очень важно, так как он позволяет не только определить число, последовательность, ориентацию необходимых элементов процесса моделирования ресурсных стратегий для осуществления товарной стратегии, но и смоделировать степень зависимости, влияния одного элемента графа на другой в процессе формирования ресурсных стратегий. Например, рис. 3 показывает, что в вершину v8 входят дуги из вершин v1 v2 и v3, что означает, что на событие по формированию стратегии ассортимента и объёмов закупок технологических ресурсов и средств труда влияют многие факторы: существующий материально-технический уровень производства и загруженность производственных мощностей, предложение ресурсов на рынках технологий и средств труда, товарные стратегии компании по ассортименту и объёму выпускаемой продукции. В вершину v9 входят дуги из вершин v3, v4, v5, v6, v8, что означает, что на стратегию по цене закупок технологий и средств труда влияют не только цены предложения на рынках технологий и средств труда и стратегии по объёму и ассортименту закупаемых технико-технологических ресурсов, но и стратегии по издержкам производства, по качеству и цене изготавливаемых товаров, точно так же на ресурсную стратегию по качеству технологий и средств труда (вершина v10) оказывает влияние не только качество предлагаемых на ресурсных рынках технико-технологических ресурсов (входящая дуга из вершины v3), но и товарные стратегии по качеству и цене (входящие дуги из вершин v5 и v6), а также ценовая ресурсная стратегия и стратегия по объёму закупок (входят дуги из вершин v8 и v9). Продолжительность жизненного цикла ресурсной стратегии зависит не только от предложения ресурсных рынков и жизненного цикла товарной стратегии, но и от привлекательности ресурсной стратегии по ассортименту, качеству и цене. В то же время от продолжительности использования ресурсов зависит ассортимент, цена и качество их закупок. Все ресурсные подстратегии влияют на окончательную технико-технологическую стратегию (вершина v12), что показывают входящие в неё дуги из вершин v8, v9, v10, v11. Аналогичные графы могут быть построены и для других ресурсных стратегий, т.е. для стратегий по обеспечению производства материальными и трудовыми ресурсами. Кроме того, с помощью графов может быть исследована и обратная зависимость, т.е. не только влияние товарной стратегии на стратегии ресурсного обеспечения производства, но и влияние материально-технической базы производства и интенсивности её использования на формируемые товарные стратегии. Эти зависимости могут быть смоделированы с помощью аналогичных графов.
Рассмотренные типы графов (рис. 1– 3) представляются универсальными для решения целого круга задач, связанных с формированием стратегий развития. Все они предназначены для моделирования процесса формирования стратегий, а потому они характеризуют определённый экономический цикл, который может быть замкнутый, как на рис. 1, 2, и незамкнутый, как на рис. 3, но все дуги рассмотренных графов ориентированы на достижение определённой вершины – цели, связанной с формированием определённой стратегии. Они позволяют определить не только последовательность операций и связи между ними в виде вершин и связывающих их дуг, но и главным образом из-за взвешенности рёбер графа оптимизировать время совершения операций цикла и достижения событий – вершин графа и цикла в целом. Подобным образом циклические графы позволяют оптимизировать и затратность формирования стратегии и её осуществления, а разновидности графа, представленного на рис. 3, позволяют ещё и определять степень влияния веса дуг на совершение того или иного события – определённой вершины графа и его цикла в целом. Все построенные графы (рис. 1–3) и любые подобные им циклические графы позволяют определить длину кратчайшего цикла, что и будет обхватом графа. Поэтому они позволяют не только смоделировать стратегию, но и оптимизировать её стоимость и продолжительность. Этим обусловлена их высокая эффективность и практическая значимость для решения широкого круга задач, связанных с формированием как товарных, так и ресурсных стратегий предприятия.
Однако когда речь идёт об использовании графов для моделирования стратегии, то следует учитывать, что наряду с процессом формирования и реализации стратегии не менее важно смоделировать стратегию как систему. На рис. 4 представлен ориентированный граф, который определяет товарную стратегию как систему, формируемую во времени и в пространстве, причём с учётом постоянно изменяющихся условий и ресурсных возможностей. Поэтому стратегия как система моделируется как динамическая система, каждый элемент которой (вершины) находятся в постоянном движении, развитии, устремляемым в бесконечность, а дуги характеризуют непрерывный поток данных и взаимосвязи между вершинами, их влияние друг на друга. Поэтому, с одной стороны, эту модель можно считать ацикличной, так как каждый её элемент стремится в бесконечность, с другой стороны, на заданном отрезке времени и в границах определённого пространства эти элементы формируют стратегию, которая способна изменяться на следующем пространственно-временном отрезке измерения, а следовательно, модель стратегии как системы (рис. 4) тоже является циклической. Однако существуют её принципиальные отличия от моделей, рассмотренных выше, которые заключаются в том, что на рис. 1–3 моделировался процесс анализа разрозненных элементов, который заканчивался процессом их синтеза в общей стратегии (товарной или ресурсной), тогда как в данной модели происходит одновременный процесс синтеза каждого элемента системы и их совокупное синергетическое влияние на синтезируемую стратегию. Вершины в данном графе являются элементами множества вершин (V) и моделируемой товарной стратегии, а дуги являются ориентированными рёбрами множества рёбер (E) и отражают, с одной стороны, обмен данными между элементами множества, а с другой стороны, характеризуют поток данных о временных, пространственных условиях, об условиях спроса и ресурсных возможностях, которые являются основой для моделирования элементов множества вершин для моделирования графом главной вершины – стратегии в целом. Каждая вершина графа образовалась в результате определённого процесса, все вершины в графе за исключением главной вершины являются, с одной стороны, начальной точкой одного процесса, а с другой стороны, конечным событием другого процесса. Тем самым отличительной чертой построенного графа (рис. 4) является то, что он является не только ориентированным, но и сильно связанным. Ориентированный граф (орграф) называется сильно связанным, если любые две его вершины сильно связаны, т.е. существует не только прямой, но и обратный путь между двумя вершинами, что обозначается стрелкой с двойным направлением связей. Другой отличительной особенностью орграфа (рис. 4) является то, что все его элементы не только являются компонентами множества, но и сами являются множествами синтезированных данных, образованных с учётом их влияния друг на друга.
Условные обозначения к рис. 4:
G4 – орграф, представленный на рис. 4; V – множество вершин; Е – множество дуг;
{v1} – вершина орграфа, характеризующая множество данных времени;
{v2} – вершина орграфа, характеризующая множество данных состояний пространства (рынков, его емкости);
{v3} – вершина орграфа, характеризующая множество данных ресурсных возможностей;
{v4} – вершина орграфа, характеризующая множество данных условий (данных потребительского спроса в разных сегментах рынка);
{v5} – вершина орграфа, характеризующая множество данных синтезированной стратегии;
({v5}; {v5}; {v5}; {v5}; {v5}) – синтезированные события – вершины, входящие в множество вершин V орграфа;
e1.2 = {v1, v2} – дуга, характеризующая путь от события v1 к событию v2, т.е. влияние времени на состояние пространства, например, емкость рынка;
e1.3 = {v1, v3} – дуга, характеризующая путь от события v1 к событию v3, т.е. влияние временных факторов на ресурсные возможности предприятия;
e1.4 = {v1, v4} – дуга, характеризующая путь от события v1 к событию v4, т.е. влияние временных факторов, например стадий позиционирования товаров, на состояние условий хозяйствования, например спроса на рынках;
e1.5 = {v1, v5} – дуга, характеризующая путь от события v1 к событию v5, т.е. в результате всех предыдущих путей, входящих в вершину v1, формируется событие – такая стратегия жизненного цикла продукта, которая влияет на окончательно формируемую товарную стратегию, входит в неё, являясь её составной частью;
e2.1 = {v2, v1} – дуга, характеризующая путь от события v2 к событию v1, т.е. связь между состоянием пространства и временем, например изменение продолжительности жизненного цикла продукта или отдельных его стадий в зависимости от емкости рынка и сегментов его позиционирования на рынке;
e2.3 = {v2, v3} – дуга, характеризующая путь от события v2 к событию v3, т.е. влияние состояния пространства, например ресурсных рынков, их ёмкости, на ресурсные возможности предприятия;
e2.4 = {v2, v4} – дуга, характеризующая путь от события v2 к событию v4, т.е. влияние состояния пространства, например ёмкости товарных рынков на потребительский спрос рынков, условия хозяйствования;
e2.5 = {v2, v5} – дуга, характеризующая путь от события v2 к событию v5, т.е. в результате всех предыдущих путей, входящих в вершину v2, формируется событие – такая стратегия пространственного позиционирования продукта на рынках, которая влияет на окончательно формируемую товарную стратегию, входит в неё, являясь её составной частью;
e3.1 = {v3, v1} – дуга, характеризующая путь от события v3 к событию v1, т.е. влияние ресурсных возможностей на временную продолжительность изготовления продукта, а также на его свойства, а следовательно, и на продолжительность его жизненного цикла предложения на рынках;
e3.2 = {v3, v2} – дуга, характеризующая путь от события v3 к событию v2, т.е. влияние ресурсных возможностей на пространственную ориентацию товарной стратегии, так как выбор рынков позиционирования товара определяется по его качеству и цене, которые зависят от качества и цены используемых при его изготовлении ресурсов;
e3.4 = {v3, v4} – дуга, характеризующая путь от события v3 к событию v4, т.е. влияние ресурсных возможностей предприятия на изменение спроса на ресурсных рынках, а также на изготовление продукции, пользующейся потребительским спросом на товарных рынках, а следовательно, и на изменение (повышение или снижение) спроса на товарных рынках;
e3.5 = {v3, v5} – дуга, характеризующая путь от события v3 к событию v5, т.е. в результате всех предыдущих путей, входящих в вершину v3, формируется событие – такая стратегия ресурсного обеспечения изготовления продукта, которая влияет на окончательно формируемую товарную стратегию (вершину v5), так как влияет на качество и цену продукта;
e4.1 = {v4, v1} – дуга, характеризующая путь от события v4 к событию v1, т.е. влияние условий – потребительского спроса на рынках на продолжительность жизненного цикла товара;
e4.2 = {v4, v2} – дуга, характеризующая путь от события v4 к событию v2, т.е. влияние условий – потребительского спроса на состояние и емкость самого рынка, а следовательно, на пространственные параметры позиционирования продуктов на рынке;
e4.3 = {v4, v3} – дуга, характеризующая путь от события v4 к событию v3, т.е. влияние условий – потребительского спроса на ресурсную обеспеченность изготовления продукта, так как в зависимости от уровня потребительских запросов к качеству продукции одни и те же ресурсные возможности фирмы могут быть как больше, так и меньше требуемых;
e4.5 = {v4, v5} – дуга, характеризующая путь от события v4 к событию v5, т.е. в результате всех предыдущих путей, входящих в вершину v4, формируется событие – такая стратегия предложения продукта по удовлетворению условий – потребительского спроса по объёму, цене, качеству продукта, которая влияет на окончательно формируемую товарную стратегию, входит в неё, являясь её составной частью;
{e1.5, e2.5, e3.5, e4.5} – множество дуг, входящих в вершину v5, т.е. несущих в неё множество данных от других вершин орграфа, т.е. от множества вершин ({v1}; {v2}; {v3}; {v4} для синтезирования товарной стратегии в вершине v5;
{e1} ∈ ({e1.2}, {e1.3}, {e1.4}, {e1.5}) – синтезированная дуга орграфа, представляющая из себя множество дуг, исходящих из вершины v1;
{e2} ∈ ({e2.1}, {e2.3}, {e2.4}, {e2.5}) – синтезированная дуга орграфа, представляющая из себя множество дуг, исходящих из вершины v2;
{e3} ∈ ({e3.1}, {e3.2}, {e3.4}, {e3.5}) – синтезированная дуга орграфа, представляющая из себя множество дуг, исходящих из вершины v3;
{e4} ∈ ({e4.1}, {e4.2}, {e4.3}, {e4.5}) – синтезированная дуга орграфа, представляющая из себя множество дуг, исходящих из вершины v4;
v5 ∈ ({e1.5}, {e2.5}, {e3.5}, {e4.5}) – синтезированная вершина v5 орграфа, в которую входит множество дуг из всех других сильно связанных вершин {v1, v2, v3, v4};
({e1}, {e2}, {e3}, {e4}) – синтезированные дуги, входящие в множество дуг орграфа.
Опираясь на условные обозначения, орграф, представленный на рис. 4, с помощью математических символов можно описать с помощью следующих формул:
(G4) (V, E) = (V, E), V≠∅ (1)
({v1, v2, v3, v4}) ∈ V(G4) (2)
({e1}, {e2}, {e3}, {e4}) ∈ E(G4) (3)
({v1, v2, v3, v4} ¬ <) ∈ E(G4). (4)
Приведённый пример показывает, что в основе любой стратегии как системы лежат четыре основных вектора орграфа, сильно связанные между собой прямыми и обратными связями, которые характеризуют единство времени, пространства, условий и возможностей для формирования стратегии. При этом вершины этих переменных элементов тоже являются синтезируемыми переменными множествами, которые способны меняться под влиянием на них данных других элементов графа, а именно каждая из вершин v1, v2, v3, v4 имеет по три входа и четыре выхода, что свидетельствует о том, что они связаны друг с другом прямыми и обратными дугами и являются компонентами сильной связанности, а все вместе формируют область сильной связанности. Каждая из вершин с помощью своих дуг имеет активный обмен данными с другими вершинами, формирует динамические множества, способные к трансформации, а на основании синтеза полученных данных формирует поток данных в конечную вершину. Поэтому из всех четырёх вершин выходит направленная дуга, которая входит в пятую вершину v5, что свидетельствует о том, что они осуществляют поток данных от себя к конечной вершине и участвуют таким образом в процессе формирования искомой стратегии на данном отрезке времени и при определённых пространственных ориентирах, с учётом существующих для них ресурсных возможностей и условий на рынках с уровнем конкуренции и запросами потребителей. Подобные графы могут широко использоваться в программировании, информатике, экономике, в том числе для моделирования потока данных, для установления взаимосвязей и взаимовлияния различных данных друг на друга и для более глубокого анализа и синтеза множества данных, так как данные графы позволяют более точно и детально моделировать стратегии, а также их дальнейшую трансформацию при изменении динамических элементов графа, лежащих в основе формирования стратегий. Это позволит повысить эффективность планирования и моделирования экономических стратегий развития, лучше связать ситуационное и стратегическое планирование в единый процесс.
Заключение
Завершая работу, следует подчеркнуть актуальность проведённого исследования и важность теоретико-методологических разработок. В теории вопроса сделан громадный шаг вперёд от определения стратегии как некой абстракции к определению стратегии как динамической системы. Сделан вывод о возможности и важности моделирования стратегии с помощью векторных методов анализа и синтеза, дано определение модели формирования стратегии как векторной модели, задающей направление экономического развития с помощью векторов и сочетающей в себе черты адаптивной, имитационной и динамической моделей. Дано теоретическое обоснование эффективности использования таких инструментов графического анализа, как графы для моделирования стратегий. В процессе исследования предложены методологические подходы к моделированию стратегий на основе графов. На рис. 1–3 представлены примеры использования графов для моделирования процессов формирования и исполнения стратегий, причём не только товарной стратегии, но и связанных с ней ресурсных стратегий. Графы для моделирования стратегий всегда являются ориентированными, т.е. орграфами. Приведённые примеры показывают, что графы являются очень эффективными инструментами для планирования как жизненных циклов изготовления и предложения товаров на рынках, так и продолжительности и затратности формируемых стратегий за счёт того, что в циклическом графе дуги могут быть взвешены как по времени, так и по стоимости. Пример графа на рис. 3 показывает, что с помощью дуг графа возможно ещё устанавливать влияние одних событий на другие, их вес и вклад в конечное событие процесса, что очень важно для планирования надёжности стратегии и прогноза её возможного изменения под влиянием различных переменных элементов графа.
На рис. 4 показан пример сильно связанного орграфа, который позволяет моделировать стратегию как систему. С помощью такого орграфа моделируются потоки данных и влияние одних событий (вершин) на другие, так как все вершины, влияющие на формирование стратегии, являются сильно связанными друг с другом прямыми и обратными дугами, они влияют друг на друга, а потому данные каждой из таких вершин синтезируются с учётом влияния на них данных других вершин. Поэтому данный орграф способен смоделировать стратегию как синергетическое множество данных, образованное на основе многократного синтеза данных каждой из вершин и их совокупного влияния на конечную вершину – формируемую товарную стратегию. Все сделанные разработки, безусловно, обладают научной новизной, позволяют сделать весомый вклад в развитие теории моделирования, планирования стратегий, в теорию и практику применения графов и графических методов анализа. Методологические рекомендации и примеры графов могут найти практическое применение и служат методологией для развития практики создания и применения подобных моделей стратегий на основе использования графов, потребность в которых по мере развития рыночного механизма хозяйствования и цифровой экономики будет возрастать.