Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Проблема дефицита государственного бюджета и ее преодоление в текущих экономических условиях могут быть рассмотрены в рамках теоретической модели смешанного финансирования дефицита государственного бюджета Бруно-Фишера [1, с. 159-169]. В отличие от модели Бруно-Фишера эмиссионного финансирования [1, с. 159-164] модель смешанного финансирования [1, с. 164-169] предполагает, что у государства имеется возможность профинансировать бюджетный дефицит, сочетая денежную эмиссию и внутренние заимствования. Следствием денежной эмиссии является ускорение инфляции. Различные аспекты эмиссионного и смешанного финансирования дефицита бюджета отражены также в экономико-математических моделях Фридмана, Кейгана, Сарджента-Уоллеса, краткий обзор которых приведен в работе [2, с. 15]. Модель Бруно-Фишера позволяет построить прогноз темпа инфляции, при котором дефицит бюджета будет покрыт при заданных экономических параметрах. Следует отметить, что в модели Бруно-Фишера в ее исходной формулировке учитывается ожидаемая инфляция. В настоящем эконометрическом исследовании ожидаемую инфляцию авторы заменяют на фактическую, исходя из предпосылки влияния текущей фактической инфляции на ожидаемую в последующий период времени (данное влияние оценено авторами статьи на основе модели адаптивных ожиданий). Таким образом, целью настоящего исследования является эконометрическая оценка влияния смешанного финансирования дефицита государственного бюджета на темп инфляции при заданной доходности облигаций федерального займа (ОФЗ).

Применяемые авторами методы исследования – формализация и математизация проблемы количественной оценки последствий смешанного финансирования бюджетного дефицита. В исследовании используются статистические данные российской экономики периода с 2000 по 2020 г.

Анализ влияния смешанного финансирования дефицита государственного бюджета на темп инфляции в модели Бруно-Фишера

Исходным уравнением модели является бюджетное ограничение государства:

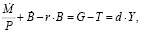(1)

M – номинальный запас денег в экономике;

M / P – реальный сеньораж за единицу времени;

P – уровень цен;

B – величина внутреннего реального (в постоянных ценах) государственного долга, запас государственных облигаций;

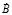– изменение внутреннего долга за единицу времени;

r = i – π– реальная процентная ставка, реальная доходность ОФЗ;

i – номинальная процентная ставка;

π – темп инфляции;

G – T – дефицит государственного бюджета (превышение государственных расходов G над налоговыми доходами T);

d – доля бюджетного дефицита относительно реального ВВП;

Y – реальный ВВП.

Для отражения связи реального запаса денежных средств и номинальной процентной ставки в модель включена функция удельного спроса на деньги (относительно реального ВВП) [1, с. 164]:

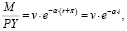(2)

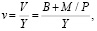(3)

V = B + M / P – сбережения потребителей, v – удельные сбережения населения относительно реального ВВП.

Параметр α модели удельного спроса на деньги (2) характеризует эластичность реального спроса на деньги по номинальной процентной ставке i = r + π:

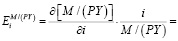
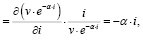(4)

где α – коэффициент полуэластичности удельного спроса на деньги по номинальной процентной ставке (показывает, на сколько процентов изменится удельный спрос на деньги при увеличении номинальной ставки процента на 1%).

В модели также учтено условие равновесия на товарном рынке для случая, когда инвестиционный спрос является частью потребительского спроса:

Y = C + G, (5)

где C – суммарный потребительский и инвестиционный спрос (на произведенные для конечного потребления товары и услуги) в экономике; G – спрос на товары и услуги со стороны государства.

Естественно предположить, что потребление C прямо пропорционально величине сбережений V и обратно пропорционально ставке процента. Также потребление снижается с ростом налогов. Поэтому в качестве спецификации модели потребительского спроса может быть рассмотрено уравнение [1, с. 165]:

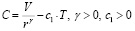(6)

Тогда из условия равновесия товарного рынка (5) с учетом уравнения (6) следует:

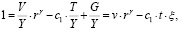
или

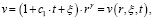
где t = T / Y, ξ = G / Y

Отметим также, что параметр γ имеет смысл эластичности удельных сбережений по реальной ставке процента:

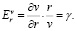(8)

То есть величина параметра γ показывает, на сколько процентов увеличатся сбережения населения в ответ на прирост ставки r на 1%.

Для перехода к удельным переменным разделим бюджетное ограничение (1) на Y. Получим уравнение:

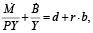(9)

где b = B / Y – отношение величины внутреннего государственного долга к ВВП.

Выражение (9) может быть переписано в виде:

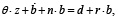(10)

где z = M / (PY) имеет смысл удельных запасов денежных средств, θ = π + n – темп прироста денежной массы в экономике (согласно количественной теории денег), n = g – темп прироста населения, совпадающий с темпом экономического роста в устойчивом состоянии экономики. Предпосылка о равенстве темпов роста населения и экономического роста предполагает, что каждое новое поколение обеспечивается постоянным подушевым доходом.

При переходе от уравнения (9) к уравнению (10) учтены соотношения:

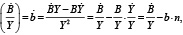(11)

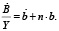(12)

Также

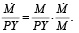(13)

В состоянии равновесия экономики b = B / Y= const, поэтому с учетом равенства θ = π + n запишем уравнение (10) в виде:

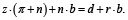(14)

В силу определения сбережений потребителей b = v –z. Поэтому:

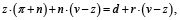(15)

или

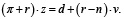(16)

С помощью полученного уравнения можно рассмотреть возможные варианты экономической политики государства в сфере финансирования дефицита государственного бюджета. Пусть целью государства является поддержание реальной процентной ставки на постоянном уровне r = r* = const. Тогда государство будет выпускать государственные облигации в таком объеме, чтобы ставка сохранялась на указанном уровне, а оставшийся дефицит будет покрывать за счет денежной эмиссии [1, с. 166]. Соотношение (16) позволяет найти темп инфляции π при заданном уровне r, при котором дефицит государственного бюджета будет покрыт.

Для нахождения темпа инфляции π уравнение (16) удобно представить в виде:

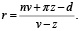(17)

С учетом (2) и (7) получим:

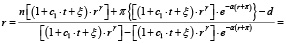
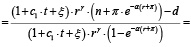
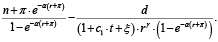
Уравнение бюджетного ограничения в равновесном состоянии экономики при фиксированной реальной процентной ставке r по облигациям принимает вид:

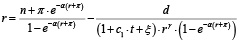. (18)

Решение уравнения (18) можно представить как точки пересечения графиков двух функций:

.

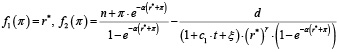Для анализа влияния последствий снижения дефицита государственного бюджета на темп инфляции воспользуемся уравнением (10), преобразованным при условии 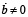к следующему виду:

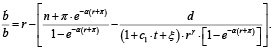(19)

Данное соотношение позволяет понять, как связаны темп прироста внутреннего долга и изменение темпа инфляции при движении к точкам равновесия A и B (рис. 1).

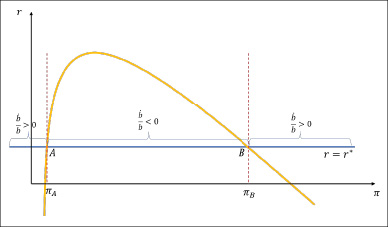
Рис. 1. Темп прироста внутреннего долга и темп инфляции Источник: построено авторами в среде Colab

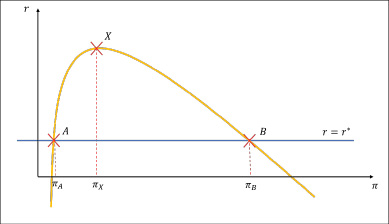
Рис. 2. Зоны влияния снижения темпа прироста внутреннего долга на поведение инфляции Источник: построено авторами в среде Colab

Таблица 1

Параметры модели Бруно-Фишера смешанного финансирования бюджета

Точкам A и B соответствуют темпы инфляции, при которых выполняется бюджетное ограничение (1), преобразованное к виду (10). Другими словами, это темпы инфляции, при которых государству удается покрыть дефицит бюджета, используя смешанное финансирование. Отметим на кривой функции f2(π) точку X максимума функции f2 (рис. 2).

Если фактический темп инфляции π меньше значения πA, то замедление темпа роста параметра b до нуля будет сопровождаться ростом темпа инфляции π до равновесного значения πA в точке A.

Если фактический темп инфляции π находится между значениями πA и πX, то замедление темпа снижения параметра b до нуля (движение от точки X к точке A) будет сопровождаться снижением темпа инфляции до равновесного уровня в точке A при значении πA.

Если фактический темп инфляции π находится между точками X и B, замедление темпа снижения параметра b до нуля (движение от точки X к точке B) будет сопровождаться ростом инфляции до точки B. Соответственно, ускорение темпа снижения параметра b позволит прийти в точку X, а далее замедление темпа снижения параметра b до нуля (движение от точки X к точке A) будет сопровождаться снижением темпа инфляции π до равновесного уровня в точке A. Таким образом, точка X – это точка изменения в управлении параметром b, темпом прироста (положительного или отрицательного) внутреннего долга.

Если фактический темп инфляции π больше темпа инфляции в точке B, ускорение темпа роста параметра b будет сопровождаться неограниченным ростом темпа инфляции. Поэтому в точке B предельная величина параметра b.

Бюджетное ограничение (18) содержит ряд параметров (табл. 1), варьирование значений которых позволяет рассматривать различные варианты экономической политики, сопровождающие реализацию смешанного финансирования государственного бюджета.

Параметры α, γ, c1 оцениваются эконометрически в рамках моделей (2) и (6) и при рассмотрении отдельных сценариев будут учтены как константы. Параметры ξ, t, d модели Бруно-Фишера отражают текущую макроэкономическую политику, могут быть оценены среднестатистически, а при рассмотрении отдельных сценариев могут варьироваться в соответствии с вероятными изменениями бюджетно-налоговой политики и величины дефицита относительно ВВП.

Для оценивания параметра α модель (2) была преобразована к виду:

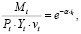(20)

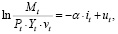(21)

где ut – случайное возмущение.

Источником эмпирической информации при оценивании модели (21) послужил массив статистических данных по финансово-экономическим переменным: денежная масса (агрегат М2) Mt , ВВП Yt, сбережения населения Vt в ценах 1999 г., а также номинальная процентная ставка it (табл. 2).

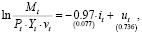
Модель (21) оценена методом наименьших квадратов (МНК) по данным в табл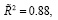. 2:

(22)

Таблица 2

Исходные данные для оценки модели удельного спроса на деньги (20)

Составлено по данным Росстата и Московской биржи [3; 4].

Учитывая экономический смысл параметра α, определенный в соотношении (4), можно сделать вывод, что при увеличении номинальной процентной ставки на 1% удельный спрос на деньги снижается на 0.97%.

Согласно коэффициенту детерминации, оцененная модель объясняет вариацию эндогенной переменной линеаризованной модели на 88%. Оценка параметра α статистически значима, т.к. t-статистика 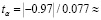12.6 > tкрит = 2.08.

Параметры γ, c1 модели (5) оценены нелинейным методом наименьших квадратов (НМНК) после преобразования к виду:

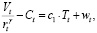(23)

где wt – случайное возмущение модели.

Для оценивания параметров γ, c1 модели (23) использован массив статистических данных по финансово-экономическим переменным: потребительские и инвестиционные расходы в экономике Ct, сбережения населения Vt, налоги Tt в ценах 2000 г., реальная ставка доходности ОФЗ rt (табл. 3).

Таблица 3

Исходные данные для оценки модели потребительского и инвестиционного спроса (23)

Составлено по данным Росстата, Федеральной налоговой службы и Московской биржи [3; 4; 5].

Оценка параметра γ была подобрана из условия минимизации остаточной суммы квадратов (RSS). Оцененное уравнение имеет вид:

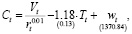
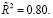(24)

Параметр γ – это эластичность удельных сбережений населения v по реальной ставке процента (7), поэтому полученная оценка параметра γ говорит о том, что при относительном увеличении реальной процентной ставки r на 1% сбережения населения возрастут на 0.01%.

Параметр c1 характеризует реакцию потребительских расходов населения в ответ на увеличение налогов на единицу (измерения) при фиксированной реальной ставке процента r. Это значит, что прирост налогов на 1 млрд руб. будет сопровождаться снижением потребительских расходов на 1.18 млрд руб. Согласно коэффициенту детерминации, оцененная модель объясняет вариацию потребительских расходов населения на 80%.

Данные для оценивания моделей (21) и (23) получены из открытых источников (табл. 4).

Таблица 4

Переменные / параметры модели Бруно-Фишера

Значения параметров ξ, t, d, а также n и r используются в модели при их текущих или средних значениях (табл. 5) и оценены на основе доступных статистических данных [3-6].

Количественная оценка темпа инфляции при выполнении условия (18) выполняется при заданном (известном) уровне доходности ОФЗ. В исследовании предполагается, что государство поддерживает ставку r на фиксированном уровне. Уравнение (18) решается относительно темпа инфляции π численно при известных значениях параметров (табл. 5). В результате решения уравнения (18) были получены два уровня темпа инфляции:

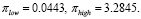
Таблица 5

Значения параметров модели Бруно-Фишера смешанного финансирования бюджета

Это значит, что при реальной доходности 10.18% ОФЗ дефицит государственного бюджета будет покрыт в условиях низкой инфляции при темпе 4.43% и в условиях гиперинфляции при темпе 328.45%.

В 2022 г. ожидаемый дефицит бюджета в Российской Федерации может составить 1600 млрд руб. [7]. Текущий темп инфляции с начала года в апреле составил 11.7% [8]. Точка фактической инфляции находится между точками A и X (πX ≈ 60%) (рис. 2). Согласно проведенному исследованию, при использовании смешанного финансирования для покрытия дефицита государственного бюджета темп инфляции 4.43% достижим при замедлении темпа снижения внутреннего долга до нуля.

Предложенный в настоящем исследовании экономико-математический инструментарий может использоваться для анализа последствий покрытия дефицита государственного бюджета при различных вариантах (сценариях) изменения экономической политики. Рассмотрим некоторые из них.

Сценарий 1. Предположим, что при реальной ставке процента по ОФЗ, равной r = 0.1018, доля бюджетного дефицита относительно ВВП d = 0.03. Если в результате реализации мер стимулирующей налоговой политики доля налогов относительно ВВП сократится до уровня t = 0.18, при этом доля государственных расходов сократится до уровня ξ = 0.36, дефицит бюджета при смешанном финансировании будет покрыт при темпе инфляции π = 0.037 (рис. 3).

Сценарий 2. Предположим теперь, что при реальной ставке процента по ОФЗ r = 0.1018 исходная доля бюджетного дефицита относительно ВВП d = 0.06. Если в результате реализации мер стимулирующей бюджетно-налоговой политики доля налогов отно-сительно ВВП сократится до уровня t = 0.18, при этом доля государственных расходов повысится до уровня ξ = 0.5, дефицит бюджета при смешанном финансировании будет покрыт при темпе инфляции π = 0.06 (рис. 4).

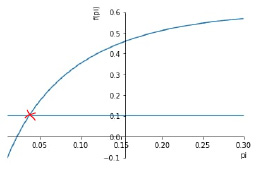
Рис. 3. Темп инфляции в условиях сценария 1 изменения бюджетно-налоговой политики Источник: построено авторами в среде Colab

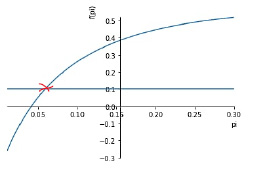
Рис. 4. Темп инфляции в условиях сценария 2 изменения бюджетно-налоговой политики Источник: построено авторами в среде Colab

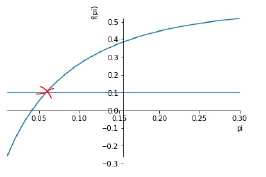
Рис. 5. Темп инфляции в условиях сценария 3 изменения бюджетно-налоговой политики Источник: построено авторами в среде Colab

Сценарий 3. Предположим теперь, что при реальной ставке процента по ОФЗ r = 0.1018 исходная доля бюджетного дефицита относительно ВВП d = 0.06. Если в результате реализации мер сдерживающей налоговой политики доля налогов относительно ВВП возрастет до уровня t = 0.22, а в результате стимулирующей бюджетной политики доля государственных расходов повысится относительно исходного уровня до ξ = 0.46, дефицит бюджета при смешанном финансировании будет покрыт при темпе инфляции π = 0.059 (рис. 5).

Оценка влияния инфляционных ожиданий на переменную потребительских и инвестиционных расходов в модели Бруно-Фишера

Оценка влияния инфляционных ожиданий на величину потребительских и инвестиционных расходов в экономике проведена в рамках модели:

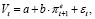(25)

где 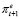– ожидаемый темп инфляции в период t + 1.

При этом предполагается, что инфляционные ожидания адаптируются к текущей инфляции с весом β:

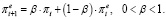(26)

Параметр β показывает, с каким весом население учитывает фактическую инфляцию, оценивая инфляцию, ожидаемую в следующем периоде. Если значение данного параметра близко к единице, скорость пересмотра инфляционных ожиданий считается высокой, и это позволяет сделать вывод о высоком уровне экономической нервозности в обществе. Модель (26) не является единственной моделью инфляционных ожиданий. Традиционные и новаторские подходы к измерению инфляционных ожиданий представлены в работах [9; 10].

Переменная 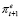не является непосредственно наблюдаемой величиной, поэтому модель (25) подлежит преобразованию. В качестве первого шага следует подставить выражение (26) вместо переменной инфляционных ожиданий в модель (25):

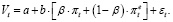(27)

В качестве второго шага для замены переменной 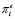фактически наблюдаемой переменной проведем преобразование модели (27). Запишем данное уравнение для момента t – 1 и умножим на множитель (1 – β):

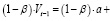(28)

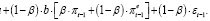
Разность уравнений (27) и (28):

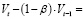
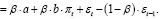(29)

Предположим также, что влияние инфляционных ожиданий на величину сбережений может отличаться в периоды усиления и ослабления кризисных ситуаций в экономике. Для эконометрической проверки данного предположения включим в уравнение (29) фиктивную переменную наклона (xt ∙ πt). Переменная xt является бинарной. Множество ее значений – {0;1}. Будем предполагать, что переменная xt принимает значение 0 в ситуации усиления кризисных ситуаций в экономике, значение 1 – в ситуации их ослабления в посткризисные годы.

Перепишем модель (29) в виде:

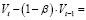
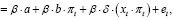(30)

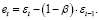
Для оценивания параметров β,a,b,δ модели (30) использованы статистические данные по переменным: сбережения населения Vt в ценах 2000 г., темп инфляции πt (табл. 6). Значения переменной xt , отражающей усиление (xt = 0) или ослабление (xt = 1) кризисных ситуаций в экономике России, были подобраны в рамках реализации нелинейного метода наименьших квадратов, исходя из максимизации коэффициента детерминации модели (30).

Оценивание модели (30) проведено с использованием нелинейного метода НМНК. Оцененное уравнение (30) имеет вид:

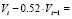
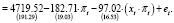(31)

Оценки 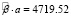, , 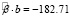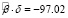статистически значимы:

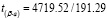≈ 24.67 > tкрит = 2.11,

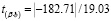≈ 9.6 > tкрит = 2.11,

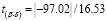≈ 5.87 > tкрит = 2.11,

Таблица 6

Исходные данные для оценки модели сбережений (30)

Оценка 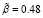подобрана из условия максимизации коэффициента детерминации модели R2. Соответственно, .

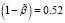Коэффициент детерминации .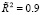

Оцененная модель адаптивных ожиданий при :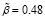

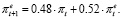(32)

Согласно модели (32) вклад фактической инфляции в формирование инфляционных ожиданий составляет 48%.

Оценки параметров a, b и δ:

если xt = 0,

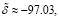
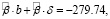
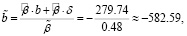если xt = 1.

Оцененная модель (25) при xt = 0 (годы усиления кризисных ситуаций в российской экономике) имеет вид:

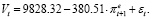(33)

Коэффициент при переменной инфляционных ожиданий 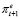означает, что с увеличением ожидаемого темпа инфляции на 1% сбережения населения понижаются на 380.51 млрд руб.

Оцененная модель (25) при xt = 1 (посткризисные годы):

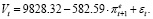(34)

Согласно модели (34) реакция сбережений населения на прирост инфляционных ожиданий существенно более выраженная по сравнению с моделью (33). С увеличением ожидаемого темпа инфляции на 1% снижение сбережений населения составляет 582.59 млрд руб.

Сравнивая модели (33) и (34), можно сделать вывод о том, что, пережив кризисные проявления экономической среды, население увеличивает свои потребительские расходы, снижая сбережения в периоды относительной стабилизации экономической ситуации.

Характеризуя экономическое поведение населения, также следует отметить относительно низкий уровень экономической нервозности согласно полученным эконометрическим оценкам. В качестве показателя экономической нервозности в контексте рассмотренных моделей в исследовании используется комплексный показатель (α ∙ β). Параметр α характеризует реакцию спроса населения и бизнеса на реальные деньги. Чем выше данный параметр, тем выше реакция на изменение номинальной процентной ставки. Параметр β отражает скорость пересмотра инфляционных ожиданий. Чем выше параметр β, тем в большей мере потребители корректируют свои инфляционные ожидания в соответствии с фактической инфляцией. Показатель нервозности населения, согласно полученным оценкам параметров моделей (22) и (32), составляет величину:

(α ∙ β) = 0.97 ∙ 0.48 = 0.4656 < 1.

Заключение

В ходе проведенного исследования на основе теоретической модели смешанного финансирования дефицита государственного бюджета Бруно-Фишера был проведен эконометрический анализ влияния смешанного финансирования на формирование темпа инфляции. Было показано, в частности, к каким изменениям темпа инфляции будут приводить варианты управления темпом прироста (положительного или отрицательного) внутреннего государственного долга, и при каких условиях достижимо низко- или высокоинфляционное состояние экономики при решении задачи покрытия бюджетного дефицита.

Проведен эконометрический анализ влияния инфляционных ожиданий на уровень сбережений населения в условиях усиления кризисных экономических ситуаций и в посткризисные периоды. Было показано, что влияние инфляционных ожиданий на сбережения существенно более выражено в условиях ослабления экономического кризиса. Оценен уровень экономической нервозности населения на основании коэффициента α, характеризующего эластичность удельного спроса на деньги по номинальной ставке процента, и на основании скорости пересмотра инфляционных ожиданий β. С учетом полученных значений данных параметров был сделан вывод о невысоком уровне экономической нервозности в российском обществе в первые два десятилетия XXI века.

Представленный в статье экономико-математический инструментарий, предназначенный для анализа последствий смешанного финансирования дефицита бюджета, может быть интересен соответствующим государственным органам при рассмотрении последствий смешанного финансирования дефицита бюджета с учетом различных вариантов бюджетно-налоговой политики.