Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Успешное развитие экономики России определяется тем, насколько динамично развиваются ее отдельные регионы. Каждый регион России, обладая своими историческими традициями, природными условиями и целым рядом специфичных факторов, имеет свои особенности и в социально-экономическом развитии. Учет таких особенностей позволяет более эффективно управлять процессами модернизации экономики, обеспечивая рост валового регионального продукта и повышение качества жизни населения региона.

Материалы и методы исследования

Любой регион России в самом общем случае можно рассматривать как сложную систему управления, подчиняющуюся действиям как внешних условий, так и внутренних факторов развития. Несмотря на особенности регионов, есть и много схожих процессов, свойственных ряду регионов. Одним из методов, позволяющих провести исследование процессов регионального развития, является кластерный анализ. Применение методов кластерного анализа позволяет на основе статистических данных по различным показателям социально-экономического развития регионов объединить отдельные регионы в целевые кластеры. Анализ таких кластеров позволяет выявлять и эффективно решать типичные проблемы регионального развития, придать ускорение экономическим процессам, сконцентрировать ресурсы на ключевых направлениях.

Методы кластерного анализа применяются уже достаточно давно, а сам термин предложен для данного вида анализа английским ученым Р. Трионом в 1939 г. Особую роль данный вид исследований получил с развитием цифровых технологий и баз данных. В современном цифровом пространстве все более заметную роль играют технологии «больших данных», где кластерный анализ занимает важную позицию. Методы кластерного анализа активно используются маркетологами, аналитиками банковской сферы, специалистами в области регионального планирования и ряде других областей науки и производства.

Методы кластерного анализа нашли широкое применение в различных областях науки и, в частности, в анализе и управлении социально-экономическими процессами. К достоинствам этих методов можно отнести универсальность, наличие большого числа алгоритмов, реализующих методы кластеризации, наличие универсальных и специализированных программных систем со встроенными сервисами кластеризации. В качестве примера использования методов кластеризации в медицинских исследованиях можно привести работы ряда авторов [1, 2]. Аналогичные методы применительно к области психологии рассматриваются в работе Т.Н. Савченко [3]. Кластерный анализ регионов России с позиций научного потенциала рассматривается в работе [4]. Целый ряд научных исследований посвящен выделению региональных кластеров по ряду критериев [5, 6]. В работах [7, 8] рассматриваются вопросы демографии и научных исследований.

Целью исследования в данной работе является выделение групп регионов со схожими социально-экономическими показателями и анализ изменений, происходящих в этих группах в течение последних лет.

Результаты исследования и их обсуждение

Успешность процедур кластеризации во многом определяется качеством данных, используемых в данном анализе. К основным требованиям, предъявляемым к выборке данных, можно отнести: отсутствие корреляции между используемыми показателями, отсутствие больших отклонений от средних значений, закон распределения факторов должен приближаться к нормальному. Кроме того, используемые в процедуре кластерного анализа показатели должны быть безразмерными и нормализованными. Таким образом, проведению кластерного анализа должны предшествовать процедуры очистки и нормализации данных.

Все методы кластеризации в качестве критерия объединения объектов кластеризации в кластер используют одну из мер близости объектов по рассматриваемому набору нормализованных признаков. Наиболее употребляемым методом оценки близости объектов можно считать квадрат евклидова расстояния. В частности, такой способ объединения объектов применяется в алгоритме k-means. Критерий объединения V вычисляется как сумма квадратов отклонений факторных признаков xi от центра j-й группировки вектора признаков μj.

,

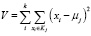где xi – факторный признак; uj – центр группировки вектора признаков; k – число кластеров.

Число кластеров задается в начале процедуры кластеризации, центры кластеров вначале формируются произвольно, а затем на каждом шаге работы алгоритма уточняются. В ходе работы алгоритма исследуемые объекты закрепляются за теми кластерами, которые обеспечивают для них минимальное расстояние до центра кластера. Оптимальным считается разбиение, обеспечивающее минимальное значение критерия V.

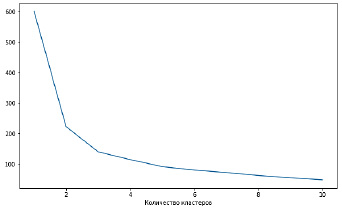
Рис. 1. Определение числа кластеров методом «локтя»

Схожими по построению алгоритма разбиения исходного множества объектов на кластеры Kj, но отличающимися выбором меры близости объектов являются такие методы, как k-medians, «расстояние городских кварталов», методы, основанные на расстоянии Чебышева.

Кроме нормализации исходных данных в начале исследования, приходится решать задачу выбора оптимального числа кластеров. Чаще всего для этих целей используется метод «локтя». Суть этого метода заключается в построении зависимости V(k) и определении точки графика, после которой уменьшение критерия оказывается незначительным (рис. 1). В приведенном ниже примере такое число кластеров равно 3.

Для решения задач кластеризации с небольшим числом факторных признаков находит применение иерархическая кластеризация, которая, в свою очередь, делится на агломеративную и дивизимную. Алгоритм агломеративной кластеризации предусматривает пошаговое объединение объектов в классы, начиная с классов с минимальным расстоянием, и поэтапное объединение отдельных классов в более крупные. В качестве наглядного результата такого объединения строится дендрограмма (рис. 2). Алгоритм дивизимной кластеризации осуществляет формирование классов путем разбиения исходного множества объектов на отдельные подмножества, и далее деление промежуточных классов продолжается до полного деления всех объектов. Как и в предыдущем случае, результат может быть проиллюстрирован дендрограммой.

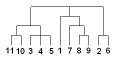
Рис. 2. Пример агломеративной кластеризации

Для выполнения алгоритмов кластеризации в данной работе рассматриваются регионы Центрального федерального округа, исключая Москву и Московскую область. Таким образом, в приведенных расчетах участвуют 16 объектов, характеризующихся набором факторных признаков по разным направлениям социально-экономического развития. Все факторы сгруппированы в четыре группы, каждая из которых имеет свой набор показателей:

1. Группа факторов общей характеристики объекта исследования:

− площадь территории p11;

− численность проживающего населения p12;

− валовой региональный продукт на душу населения p13;

− объем инвестиций p14.

2. Группа социальных факторов:

− уровень безработицы p21;

− фактическое потребление на душу населения p22;

− среднедушевой доход p23;

− число безработных p24;

− число заболевших на 10000 населения p25;

− количество коек на 10000 населения p26.

3. Характеристики инновационности:

− число организаций, занимающихся научными исследованиями, p31;

− затраты на научные исследования p32;

− использование инновационных производственных технологий p33;

− инновационная активность p34;

− наличие веб-представительств p35;

− подготовка бакалавров и специалистов p36.

4. Сферы деятельности:

− объем сельскохозяйственного производства p41;

− общий оборот сельскохозяйственной продукции p42;

− число предприятий обрабатывающей промышленности p43;

− объем обрабатывающей промышленности p44;

− транспортно-логистическая отрасль p45;

− объем транспортно-логистической отрасли p46;

− торговля p47;

− объем торговой отрасли p48.

В качестве данных для анализа использованы данные статистических наблюдений [7] за 2015, 2018 и 2020 гг. Кластерный анализ выполняется c использованием пакетов программ Python и пакете анализа RStudio. На первом этапе анализа выполняется нормализация данных с использованием формулы

,

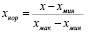где хмин и хмах определяются по каждому факторному признаку исходных таблиц данных. Как результат нормализации получаем четыре фрейма данных для каждой группы показателей в диапазоне [0–1].

Следующим шагом анализа является проведение корреляционного анализа с целью исключения факторных признаков, имеющих высокую корреляционную связь. Для реализации алгоритма воспользуемся пакетом Scipy из набора Python, а также пакет визуализации Seaborn.

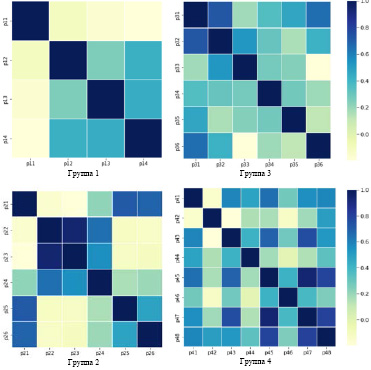
Рис. 3. Результаты корреляционного анализа

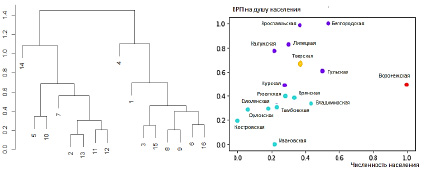
Рис. 4. Дендрограмма агломеративной кластеризации первой группы показателей

Анализ приведенных выше корреляционных диаграмм позволяет сделать следующие выводы. По первой группе факторных признаков высокой корреляционной зависимости не наблюдается. По второй группе наблюдается высокая корреляционная зависимость между фактическим потреблением и доходами на душу населения. Кроме того, достаточно высока связь между уровнем безработицы и числом заболевших на 10000 населения. Для дальнейшего анализа убираем факторные признаки p22 и p25. По третьей группе в силу высокой связи между факторами p31 и p32 оставляем для дальнейшего анализа факторный признак p32. По четвертой группе факторных признаков наблюдаем высокую корреляцию показателей p47 и p48 с остальными признаками, поэтому исключаем их из дальнейшего анализа.

Для проведения кластеризации по каждой группе факторных признаков в данной работе использовался алгоритм k-means в сочетании с агломеративной кластеризацией. На рис. 4 представлена дендрограмма для первой группы показателей.

Проведенные расчеты позволили выбрать наиболее рациональное число кластеров в разбиении. По всем четырем группам решается задача с четырьмя кластерами. Обозначим имена кластеров в каждой из четырех групп через Ai; Bi; Ci; Di, где i – номер группы факторных признаков. Проанализируем формирование кластеров в каждой группе факторов и признаки принадлежности к кластеру (табл. 1).

Результаты кластерного анализа по всем группам и периодам сведены в табл. 2.

Проведя комплексный анализ итоговой таблицы, можно проследить динамику социально-экономического развития регионов по рассматриваемым направлениям деятельности. Субъекты ЦФО условно можно распределить на 4 группы.

К первой группе можно отнести Воронежскую область – безусловного лидера по всем направлениям развития.

Вторую группу формируют Тверская, Белгородская, Калужская, Липецкая, Тульская, Ярославская области, имеющие в основном показатели выше среднего и максимальные по отдельным направлениям, обладающие потенциалом для дальнейшего роста и развития. Данные субъекты показывают стабильный рост ВРП. Анализ показывает, что следует усилить работу по реализации комплекса мер по увеличению инновационной составляющей экономики, привлечения инвестиций в экономику регионов.

В третьем кластере расположились Брянская, Владимирская, Курская, Рязанская, Тамбовская и Смоленская области, которые можно охарактеризовать как регионы с неравнозначным и нестабильным развитием. Их можно назвать умеренно стабильными. Основными направлениями деятельности по стабилизации социально-экономической ситуации в данной группе является деятельность по расширению и модернизации промышленного производства, повышению инновационной активности.

Четвертый кластер объединяет Ивановскую, Костромскую и Орловскую области, имеющие средние и ниже среднего показатели по большей части исследуемых факторов. Данный кластер характеризуется статичным или слабым социально-экономическим развитием.

Таблица 1

Характерные признаки объектов кластеризации в каждом кластере

Таблица 2

Результаты кластеризации 16 объектов по четырем группам и трем периодам

Таким образом, использование кластерного анализа позволяет анализировать влияние отдельных факторов на сбалансированность социально-экономического развития региона, что очень важно учитывать при разработке стратегий, программ и формировании социально-экономической политики региона. Кроме того, появляется возможность оценивать в перспективе последствия изменения показателей.

Выводы

По результатам исследования сделаны следующие выводы:

− Методы кластерного анализа являются эффективным инструментом при осуществлении комплексного анализа социально-экономического развития регионов.

− Проведенные исследования позволили выявить как общие особенности, так и различия в показателях исследуемых объектов, что позволяет оптимальным образом выстраивать стратегию и планы развития регионов.

− Анализ распределения регионов по отдельным кластерам за последние пять лет позволил оценить динамику развития регионов.

− Выделенные группы признаков при определении кластеров позволяют дать всестороннюю характеристику регионам.