Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

При эконометрическом моделировании весьма важными являются вопросы оценки качества построенных моделей, выбора оптимальных моделей. Существуют различные подходы к решению этих вопросов. Будем рассматривать проблемы, связанные только с оценкой качества линейных регрессионных моделей. Пусть спецификация регрессионной модели имеет вид

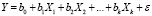, (1)

где Y – эндогенная (зависимая) переменная, k – количество регрессоров, ε – случайная составляющая эндогенной переменной (случайное возмущение), которая не может быть объяснена значениями объясняющих переменных 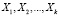. Количество параметров модели равно m, m= k+1.

Обычно считают, что «модель считается хорошей со статистической точки зрения, если она адекватна и достаточно точна» [1, с. 310]. Если вопросы оценки точности модели, как правило, не вызывают разночтений, то по оценке адекватности не существует единого мнения. Существует распространённое мнение, что проверка адекватности модели означает проверку гипотезы о равенстве нулю всех коэффициентов регрессии (Н0: b1 = b2 =…bk = 0), т.е. проверяется значимость модели регрессии в целом [2, 3]. Если основная гипотеза Н0 принимается, то модель считается неадекватной. Если же основная гипотеза отклоняется, то модель можно считать адекватной только после проверки выполнения предпосылок МНК относительно остатков: равенство нулю математического ожидания, гомоскедастичность, случайность и независимость, соответствие нормальному закону распределения. Если эти предпосылки не выполняются, то модель признается неадекватной.

Другое представление об адекватности модели заключается в проверке качества прогнозов, получаемых на базе обучающей выборки путем сравнения этих прогнозов с реальными значениями из контролирующей выборки [4–6]. При этом следует иметь в виду, что такая проверка осуществляется только при выполнении предпосылок МНК.

Подход, когда модель обучается на одном образце данных («обучающем наборе») и оценивается вне выборки на так называемом «тестовом наборе», известен как перекрестная проверка (cross-validation, сокращенно CV).

Целью работы является анализ разных подходов к оценке адекватности и выбору линейных регрессионных моделей, предназначенных для прогнозирования, и исследование инструментария для проведения перекрестной проверки моделей, построенных на пространственных наблюдениях.

Материалы и методы исследования

Использование интервальных прогнозов для проверки спецификации модели. Если значения эндогенной переменной из контролирующей выборки попадают в прогнозные интервалы, то спецификация модели подтверждается.

Исследуем зависимость количества безработных в среднем в млн чел в России от заявленной потребности в работниках (в тыс. чел.) [7].

По данным (табл. 1) за период с 2001 по 2019 г. (обучающая выборка) построена регрессионная модель зависимости количества безработных в среднем (Y) от заявленной потребности в работниках – X: 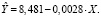В качестве контролирующей выборки используются данные за 2020 г.

Для оценки прогноза 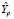на 2020 г. по модели 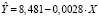используем значения X за 2020 г. и получим точечный прогноз :

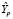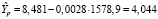млн чел.

Ошибка прогноза sp, необходимая для вычисления доверительного интервала 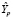, вычисляется по формуле:

,

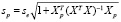где 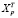– строка матрицы Х, относящаяся к 2020 г., 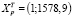, se – стандартная ошибка модели. Вычисление ошибки прогноза sp в Excel с использованием матричных функций МУМНОЖ, ТРАНСП, МОБР является несложной, но затратной по времени процедурой. Последовательность вычислений приведена на рис. 1. Как видим, sp = 0,461. Значение t-статистики tkp(0,05;17) равно 2,11,

НГр = 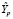– tkp · sp = 4,044 –2,11 · 0,461 = 3,07 (НГр – нижняя граница)

ВГр = 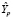+ tkp · sp = 4,044 + 2,11 · 0,461=5,02 (ВГр – верхняя граница)

Так как значение эндогенной переменной из контролирующей выборки Y(2020), равное 4,3, попадает в 95%-ый доверительный интервал (3,07 5,02), то модель признаётся адекватной.

Таблица 1

Исходные данные

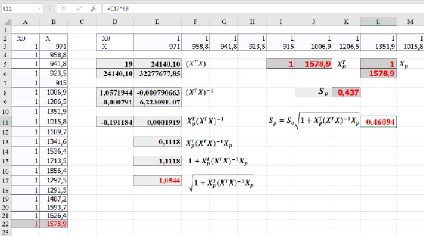
Рис. 1. Вычисление ошибки прогноза sp в Excel

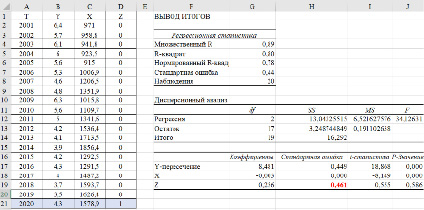
Рис. 2. Оценка параметров модели с фиктивной переменной: 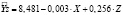(0,449) (0,000) (0,461)

Для вычисления стандартных ошибок прогнозов воспользуемся методом Салкевера [8, 9]. В этом методе для оценки стандартной ошибки прогноза на момент t = n + 1 в матрицу регрессоров добавляется строка Xn+1 и столбец фиктивных переменных Z, содержащий нули для всех наблюдений, кроме (n + 1)-го, в котором фиктивная переменная равна 1. На рис. 2 приведена таблица исходных данных и результаты оценки параметров модели с фиктивной переменной. Стандартная ошибка оценки параметра при фиктивной переменной равна стандартной ошибке прогноза. В нашем случае она равна sp = 0,461.

Использование перекрестной проверки для оценки адекватности модели и выбора лучшей модели

Рассмотрим применение одного из самых простых методов перекрестной проверки LOOCV (Leave One Out Cross Validation) – перекрестная проверка с исключением одного наблюдения. В LOOCV каждое наблюдение рассматривается как контролирующий набор, а остальные (n–1) наблюдений – как обучающий набор. Подгонка модели и прогнозирование повторяется n раз. Критерий перекрестной проверки CV может быть вычислен путем выполнения n регрессий, в которых каждый раз пропускается одно наблюдение, а все остальные используются для прогнозирования его значения. Сумма n квадратов ошибок прогноза – это и есть CV – та статистика, которая используется для оценки качества модели. Однако в вычислении n регрессий нет необходимости. Эту статистику можно найти иначе, воспользовавшись так называемой матрицей шляп H от английского слова hat. Матрица H равна

H = X (XT X)–1 XT . (2)

Покажем, как ошибку прогноза i-го наблюдения зависимой переменной по уравнению регрессии без i-го наблюдения можно вычислить, зная лишь ошибку прогноза этого наблюдения по уравнению регрессии с полным набором наблюдений и диагональные элементы матрицы H.

Пусть X, Y – матрица регрессоров и вектор значений зависимой переменной, X[i], Y[i] получены из X, Y после удаления из них i-го наблюдения, 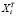– i-я строка X и пусть 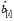= 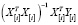– оценка вектора коэффициентов регрессии b без i-го наблюдения.

Тогда ошибка прогноза i-го наблюдения, вычисленная по регрессии без i-го наблюдения, равна 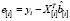. Очевидно, произведение 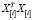можно представить в виде 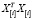=(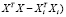. По формуле Шермана – Моррисона – Вудбери [10]

=+.

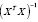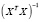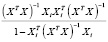Но произведение 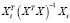равно диагональному элементу hi матрицы H, 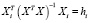. Тогда

=+.

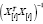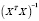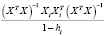Учитывая также, что 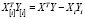, получаем

+ ]() =

= () =

= ( = ( = ,

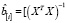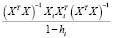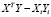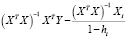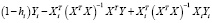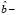
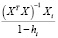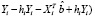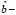
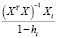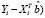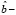
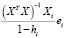где 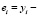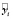= 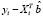– ошибка прогноза i-го наблюдения по уравнению регрессии с полным набором переменных. Тогда

= ( ) =

= + = + =

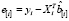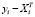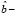
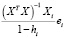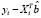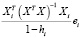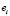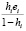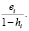
Таким образом, получили, что ошибка прогноза i-го наблюдения по регрессии без i-го наблюдения e[i] равна e[i] = ei / (1 – hi). Полученная формула существенно упрощает процедуру вычисления критерия перекрестной проверки CV,

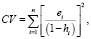(3)

где hi – диагональный элемент матрицы H.

Для пояснения смысла матрицы Н запишем предсказываемые моделью значения эндогенной переменной Y в виде

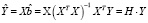
или, в координатной форме,

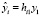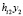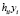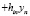++…++…, i=1,…n.

Диагональные элементы матрицы H изменяются от нуля до единицы и в сумме равны числу параметров модели m. Показатель hii (диагональный элемент hii матрицы H отражает расстояние между точкой с координатами Xi и центром данных. Если значение hi близко к нулю, то это означает, что i-я точка Xi располагается недалеко от центра, если hi близка к единице, то i-я точка является удаленной. Считается, что наблюдение оказывает существенное влияние на параметры модели, если 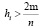. Чем дальше от центра системы находится наблюдение, тем больше его влияние на оценку коэффициентов регрессии. Такие наблюдения называют точками разбалансировки (леверидж). Показатель hi является удобным индикатором того, является ли i-е наблюдение точкой разбалансировки. Именно диагональные значения матрицы Н используются при вычислении статистики CV. При выборе лучшей модели из нескольких выбирается та, у которой меньше значение статистики CV.

Результаты исследования и их обсуждение

Применим метод LOOCV для выбора лучшей модели при моделировании зависимости рождаемости (число родившихся на 1000 чел.) [11] от индекса цен (Индексы потребительских цен на товары и услуги 2020 г.) по данным 16 регионов РФ [12].

Построенная по всем наблюдениям (табл. 2) модель имеет вид:

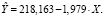
Из приведенного протокола (рис. 3) можно сделать вывод, что параметры модели значимы, коэффициент детерминации достаточно высокий 0,87. Для выбранных регионов увеличение индекса цен на один процент приводит в среднем к уменьшению числа родившихся примерно на два человека.

Для оценки качества этой модели построено 16 уравнений регрессии, в каждом из которых последовательно удалялось по одному наблюдению. Оценки параметров этих моделей, прогноз на 16-е наблюдение, ошибка прогноза и квадрат ошибки приведены в табл. 2. Сумма квадратов ошибок – это и есть CV – равна 14,824.

Другой подход к вычислению статистики CV с помощью Н матрицы приведен в табл. 3 и 4. В табл. 3 приведен фрагмент матрицы Н, вычисленной с помощью матричных преобразований по формуле (2).

Таблица 2

Исходные данные и результаты перекрестной проверки по 16 моделям

Рис. 3. Оценка параметров модели регрессии зависимости рождаемости от индекса цен на данных 16 регионов РФ

В табл. 4 приведены остатки, полученные при построении модели регрессии по всем наблюдениям, диагональные элементы матрицы Н и CV критерий.

Метод перекрестной проверки с исключением одного наблюдения реализован в Gretl. При анализе построенной модели (рис. 3) в меню следует выбрать значимость наблюдений (рис. 4) и в качестве дополнительной информации для команды leverage будет получен критерий CV (табл. 5).

Таблица 3

Фрагмент матрицы Н

Таблица 4

Вычисление критерия перекрестной проверки на основе матрицы Н

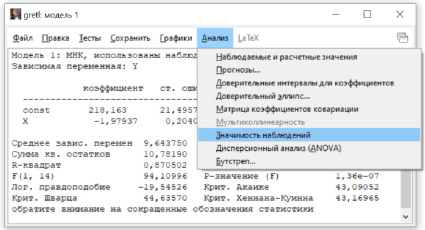
Рис. 4. Оценка параметров модели регрессии в Gretl и выбор вида анализа построенной модели

Таблица 5

Вычисление критерия перекрестной проверки в Gretl

Остатки леверидж Воздействие DFFITS

u 0<=h<=1 u*h/(1-h)

1 -0,7518 0,093 -0,07728 -0,286

2 -0,71221 0,095 -0,074644 -0,273

3 -1,1654 0,073 -0,09197 -0,402

4 0,71603 0,160 0,1365 0,386

5 -0,42994 0,086 -0,040616 -0,153

6 -1,0009 0,065 -0,069815 -0,316

7 1,6911 0,198 0,41773 1,260

8 -0,50499 0,072 -0,039302 -0,163

9 0,22738 0,097 0,024302 0,086

10 0,26903 0,090 0,02662 0,098

11 -0,16457 0,080 -0,014278 -0,056

12 -0,22621 0,177 -0,048696 -0,127

13 0,42698 0,131 0,064405 0,197

14 -0,67528 0,276* -0,25712 -0,554

15 1,3082 0,139 0,21044 0,687

16 0,99255 0,168 0,20025 0,569

(‘*’ указывает на точку левериджа)

Критерий перекрестной проверки = 14,8237

Затем в Gretl была построена двухфакторная модель, спецификация которой имеет вид:

.

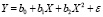После оценки параметров модели в Gretl был вычислен критерий перекрестной проверки CV. Несмотря на то, что коэффициент детерминации двухфакторной модели 0,88 больше коэффициента детерминации однофакторной модели (0,87), а стандартная ошибка меньше (0,81 против 0,88), критерий перекрестной проверки CV, равный 20,65, больше значения CV для однофакторной модели, равного 14,82. В качестве лучшей модели для прогнозирования выбираем однофакторную модель.

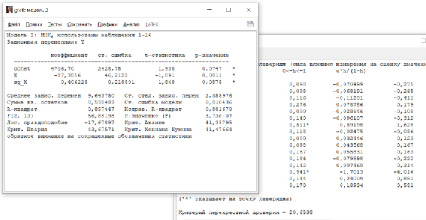
Рис. 5. Оценка параметров и критерия перекрестной проверки двухфакторной модели

Заключение

Рассмотрев некоторые аспекты оценки качества линейных регрессионных моделей, а именно проблему проверки адекватности моделей, можно сделать следующие выводы.

Оценка качества моделей регрессии должна выполняться по нескольким направлениям: оценка значимости всего уравнения регрессии, оценка значимости параметров модели регрессии, оценка точности модели, проверка выполнения предпосылок МНК, и только при положительных результатах по этим пунктам осуществлять проверку качества прогнозов, получаемых на базе обучающей выборки путем сравнения этих прогнозов с реальными значениями из контролирующей выборки, т.е. проверять адекватность модели, ее способность к построению точных прогнозов.

В качестве инструментария могут использоваться различные методы перекрестной проверки, реализованные в R или Gretl, а при небольших выборках можно использовать Excel.